辽宁省抚顺市东洲区2022年九年级模拟检测（一）数学试题

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列方程中是一元二次方程的是（）

A、 $x y + 2 = 1$ B、 $x^{2} + 2 x - 9 = 0$ C、 $\frac{1}{x^{2}} - 1 = 0$ D、 $a x^{2} + b x + c = 0$

查看试题解析
2. 下列四个图形是中心对称图形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 用配方法解方程 $x^{2} - 6 x = 1$ ，配方正确的是（）

A、 $(x - 3)^{2} = 10$ B、 $(x - 3)^{2} = 9$ C、 $(x - 6)^{2} = 8$ D、 $(x - 6)^{2} = 10$

查看试题解析
4. 小明不慎把家里的圆形镜子打碎了，其中三块碎片如图所示，三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是（）

A、① B、② C、③ D、均不可能

查看试题解析
5. 一只小鸟自由地在天空中飞翔，然后随意的落在如图所示的某个方格中（每个方格除颜色外完全一样），那么小鸟停在阴影区域中的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
6. 关于x的一元二次方程 $k x^{2} + 3 x - 1 = 0$ 有实数根，则 $k$ 的取值范围是（）

A、 $k \leq - \frac{9}{4}$ B、 $k \geq - \frac{9}{4}$ 且 $k \neq 0$ C、 $k \geq - \frac{9}{4}$ D、 $k > - \frac{9}{4}$ 且 $k \neq 0$

查看试题解析
7. 一套书共有上，中，下三册，将它们任意摆放到书架的同一层上，这三册书从左到右恰好成上，中，下顺序的概率为（　　）

A、 $\frac{1}{12}$ B、 $\frac{1}{6}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
8. 如图，若AB是⊙O的直径，CD是⊙O的弦，∠ABD＝65°，则∠BCD的度数为（）

A、55° B、45° C、35° D、25°

查看试题解析
9. 如图，圆锥的底面半径OB＝5，高OC＝12，则这个圆锥的侧面积是（）

A、30π B、45π C、65π D、80π

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c$ （a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b²； ②3a+c＞0；③方程 $a x^{2} + b x + c = 0$ 的两个根是x₁=﹣1，x₂=3；④当y＞0时，x的取值范围是﹣1＜x＜3⑤当x＞0时，y随x的增大而减小.其中结论正确的个数是（）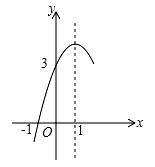

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 二次函数 $y = (x - 1)^{2}$ 的顶点坐标为．

查看试题解析
12. 已知点A（1，a）、点B（b，2）关于原点对称，则a+b的值为．

查看试题解析
13. 抛物线y＝﹣ $\frac{1}{2}$ x²向上平移1个单位长度得到抛物线的解析式为．

查看试题解析
14. 已知x=3是方程x²﹣6x+k=0的一个根，则k= ．

查看试题解析
15. 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球个．

查看试题解析
16. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，正六边形的周长是12，则 $⊙ O$ 的半径是.

查看试题解析
17. 如图，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC＝5，BD＝4，则△ADE的周长是．

查看试题解析
18. 如图，抛物线解析式为y＝x² ，点A₁的坐标为（1，1），连接OA₁；过A₁作A₁B₁⊥OA₁ ，分别交y轴、抛物线于点P₁、B₁；过B₁作B₁A₂⊥A₁B₁分别交y轴、抛物线于点P₂、A₂；过A₂作A₂B₂⊥B₁A₂ ，分别交y轴、抛物线于点P₃、B₂…；则点P_n的坐标是．

查看试题解析

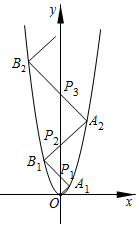
三、解答题

19. 解方程：

(1)、 $2 (x^{2} - 4 x) + 3 = 0$ （公式法）

(2)、 $(x + 1) (x + 2) = 2 x + 4$

查看试题解析
20. 为庆祝建党100周年，某大学组织志愿者周末到社区进行党史学习宣讲，决定从A ， B ， C ， D四名志愿者中通过抽签的方式确定两名志愿者参加．抽签规则：将四名志愿者的名字分别写在四张完全相同不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字，

(1)、“A志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；

(2)、请你用列表法或画树状图法表示出这次抽签所有可能的结果，并求出A ， B两名志愿者被选中的概率．

查看试题解析
21. 如图，在平面直角坐标系中，A(3，3)，B(4，0)，C(0，﹣1)．

(1)、以点C为旋转中心，把 $△$ ABC逆时针旋转90°，画出旋转后的图形 $△$ $A^{'} B^{'}$ C；

(2)、在（1）的条件下，
①点A经过的路径 $\overset{⌢}{A A^{'}}$ 的长为（结果保留π）；
②则此时B'点的坐标为．

查看试题解析
22. 某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为18米（如图所示），设这个苗圃园垂直于墙的一边长为 $x$ 米．

(1)、若苗圃园的面积为72平方米，求 $x$ ；

(2)、若平行于墙的一边长不小于8米，求这个苗圃园的面积的最大值和最小值．

查看试题解析
23. 如图，PB切⊙O于点B，连接PO并延长交⊙O于点E，过点B作BA⊥PE交⊙O于点A，连接AP，AE．

(1)、求证：PA是⊙O的切线；

(2)、如果AB＝DE，OD＝3，求⊙O的半径．

查看试题解析
24. 某商场经营某种品牌的玩具，购进时为每件30元，现在的售价为每件40元，每周可卖出150件．市场调查反映：如果每件的售价每涨2元，那么每周少卖10件．设每件涨价 $x$ 元，每周的销售量为 $y$ 件．

(1)、求 $y$ 与 $x$ 的函数关系式；

(2)、当该玩具每件售价为多少元时，该商场才能在一周内获得最大利润？最大利润是多少元？

查看试题解析
25. 如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连AF. 取AF的中点M，EF的中点N，连接MD、MN．

(1)、请判断MD与MN之间的数量关系，直接写出结论；

(2)、将图1中的直角三角板ECF绕点C顺时针旋转180°得到图2，其他条件不变，则（1）中的结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

(3)、连接DN，若AB＝3，CE＝2，将图1中的直角三角板ECF绕点C在平面内自由旋转，其他条件不变，请直接写出△DMN面积的最大值和最小值．

查看试题解析
26. 如图，抛物线 $y = a x^{2} + b x + \frac{3}{2}$ 经过A（ $- 1 ， 0$ ），B（ $4 ， - \frac{5}{2}$ ）两点，直线AB与 $y$ 轴交于点C．

(1)、求抛物线的解析式；

(2)、点M在抛物线上，点N在直线AB上，当M，N关于原点O成中心对称时，求点N的坐标；

(3)、设P是抛物线对称轴上的一点，点Q在抛物线上，以A，B，P，Q为顶点的四边形能否成为平行四边形？若能，请直接写出点P的坐标；若不能，请说明理由．

查看试题解析