江西省新余市2022年中考第一次模拟数学试题

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣2022的倒数是（）

A、 $- \frac{1}{2022}$ B、 $\frac{1}{2022}$ C、﹣2022 D、2022

查看试题解析
2. 2020年初，新冠病毒引发疫情．一方有难，八方支援．危难时刻，全国多家医院纷纷选派医护人员驰援武汉．下面是四家医院的图案标志，其中轴对称图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $2 a (3 a - 1) = 6 a^{2} - 1$ C、 ${(3 a^{2})}^{2} = 6 a^{4}$ D、 $x^{3} + x^{3} = 2 x^{3}$

查看试题解析
4. 如图， $O P / / Q R / / S T$ 下列各式中正确的是（）

A、 $∠ 1 + ∠ 2 + ∠ 3 = 180^{\circ}$ B、 $∠ 1 + ∠ 2 - ∠ 3 = 90^{\circ}$ C、 $∠ 1 - ∠ 2 + ∠ 3 = 90^{\circ}$ D、 $∠ 2 + ∠ 3 - ∠ 1 = 180^{\circ}$

查看试题解析
5. 如图，抛物线 $y = a x^{2} + b x + c$ 交x轴于 $(- 1 ， 0)$ ， $(3 ， 0)$ 两点，则下列判断中，不正确的是（）

A、图象的对称轴是直线 $x = 1$ B、当 $x > 2$ 时，y随x的增大而减小 C、当 $- 1 < x < 1$ 时， $y < 0$ D、一元二次方程 $a x^{2} + b x + c = 0$ 的两个根是 $- 1$ 和3

查看试题解析
6. 如图，正方形ABCD中，AB=6，将△ADE沿AE对折至△AEF，延长EF交BC于点G，G刚好是BC边的中点，则ED的长是（）

A、1 B、1.5 C、2 D、2.5

查看试题解析

二、填空题

7. 因式分解： $1 - y^{2} =$ ．

查看试题解析
8. 2021年10月11日，联合国《生物多样性公约》缔约方大会第十五次会议（COP15）在昆明正式拉开帷幕.在多彩的生物界，科学家发现世界上最小的开花结果植物是澳洲的出水浮萍，其质量仅有0.000000076克，0.000000076用科学记数法表示是．

查看试题解析
9. 若方程 $x^{2} - 2 x - 3 = 0$ 两根为 $α$ 、 $β$ ，则 $α^{2} + β^{2} =$ ．

查看试题解析
10. 已知圆锥的母线长为5，侧面积为20 $π$ ，则这个圆锥的底面圆的半径为.

查看试题解析
11. 如图，图①是棱长为4cm的立方体，沿其相邻三个面的对角线(虚线)裁掉一个角，得到如图②的几何体，则一只蚂蚁沿着图②几何体的表面，从顶点A爬到顶点B的最短距离为 cm.

查看试题解析
12. 如图，矩形ABCD中，AB＝6，AD＝4 $\sqrt{3}$ ，点E是BC的中点，点F在AB上，FB＝2，P是矩形上一动点．若点P从点F出发，沿F→A→D→C的路线运动，当∠FPE＝30°时，FP的长为．

查看试题解析

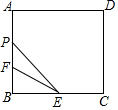
三、解答题

13.

(1)、计算： $| - 2 | - 3 t a n 60 ° + {(2 \sqrt{3})}^{0} + \sqrt{12}$

(2)、解方程： $\frac{x}{x + 2} - 1 = \frac{8}{x^{2} - 4}$

查看试题解析
14. 以下是圆圆解不等式组
${\begin{array}{l} 2 (1 + x) > - 1 ① \\ - (1 - x) > - 2 ② \end{array}$
的解答过程．
解：由①，得 $2 + x > - 1$ ，
所以 $x > - 3$ ．
由②，得 $1 - x > 2$ ，
所以 $- x > 1$ ，
所以 $x > - 1$ ．
所以原不等式组的解是 $x > - 1$ ．
圆圆的解答过程是否有错误？如果有错误，写出正确的解答过程．

查看试题解析
15. 为庆祝“三八妇女节”，某地举行歌咏比赛，歌曲有：《我爱你，中国》，《歌唱祖国》，《我和我的祖国》（分别用字母A，B，C依次表示这三首歌曲）．比赛时，将A，B，C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，甲先从中随机抽取一张卡片，放回后洗匀，再由乙从中随机抽取一张卡片，进行歌咏比赛．

(1)、甲抽中歌曲《我和我的祖国》的概率是；

(2)、试用画树状图或列表的方法表示所有可能的结果，并求出甲和乙抽中不同歌曲的概率．

查看试题解析
16. 如图，已知多边形ABCDEF中，AB＝AF ， DC＝DE ， BC＝EF ， ∠ABC＝∠BCD ．请仅用无刻度的直尺，分别按下列要求画图．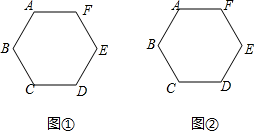

(1)、在图①中，画出一个以BC为边的矩形；

(2)、在图②中，若多边形ABCDEF是正六边形，试在AF上画出点M ，使得AM＝ $\frac{1}{4}$ AF ．

查看试题解析
17. 为了解某市九年级学生参加社会实践活动情况，随机抽查了某县部分九年级学生第一学期参加社会实践活动的天数，并用得到的数据绘制了两幅统计图，下面给出了两幅不完整的统计图．
请根据图中提供的信息，回答下列问题：

(1)、a= ▲ ，请补全条形图；

(2)、在这次抽样调查中，众数是天，中位数是天；

(3)、如果该县共有九年级学生2000人，请你估计“活动时间不少于7天”的学生人数大约有多少人？

查看试题解析
18. 如图，一次函数y=kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y= $\frac{n}{x}$ （n为常数，且n≠0）的图象在第二象限交于点C．CD⊥x轴，垂足为D，若OB=2OA=3OD=12．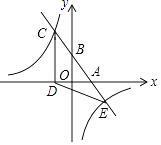

(1)、求一次函数与反比例函数的解析式；

(2)、记两函数图象的另一个交点为E，求△CDE的面积；

(3)、直接写出不等式kx+b≤ $\frac{n}{x}$ 的解集．

查看试题解析
19. 如图所示，一辆单车放在水平的地面上，车把头下方 $A$ 处与坐垫下方 $B$ 处在平行于地面的同一水平线上， $A$ ， $B$ 之间的距离约为 $49 c m$ ，现测得 $A C$ ， $B C$ 与 $A B$ 的夹角分别为 $45 °$ 与 $68 °$ ，若点 $C$ 到地面的距离 $C D$ 为 $28 c m$ ，坐垫中轴 $E$ 处与点 $B$ 的距离 $B E$ 为 $4 c m$ ，求点 $E$ 到地面的距离（结果保留一位小数）.（参考数据： $s i n 68 ° \approx 0.93$ ， $c o s 68 ° \approx 0.37$ ， $c o t 68 ° \approx 0.40$ ）

查看试题解析
20. 某学校在开展“学习雷锋精神，争做时代标杆”的征文活动中，计划对获得一、二等奖的学生分别奖励一支钢笔，一本笔记本．已知购买3支钢笔和2本笔记本共52元，购买5支钢笔和4本笔记本共92元．

(1)、钢笔和笔记本的单价分别为多少元?

(2)、经与文具店协商，购买钢笔超过30支时，每增加1支，单价降低0.1元；超过50支，均按购买50支的单价出售，笔记本一律按原价销售．学校计划奖励一、二等奖学生共计100人，其中一等奖的人数不少于30人，且不超过60人，这次奖励一等奖学生多少人时，购买奖品总金额最少，最少为多少元?

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， D为AB边上的一点，以AD为直径的 $⊙ O$ 交BC于点E，交AC于点F，过点C作 $C G ⊥ A B$ 于点G，交AE于点H，过点E的弦EP交AB于点Q（EP不是直径），点Q为弦EP的中点，连结BP，BP恰好为 $⊙ O$ 的切线．

(1)、求证：BC是 $⊙ O$ 的切线；

(2)、求证：AE平分 $∠ C A B$ ；

(3)、若 $A Q = 10$ ， $E Q = 5$ ， $\frac{H G}{A G} = \frac{1}{2}$ ，求四边形CHQE的面积．

查看试题解析
22. 综合与实践
如图1，已知点G在正方形ABCD的对角线AC 上，GE⊥BC，垂足为E，GF⊥CD，垂足为F．

(1)、（证明与推断）
①四边形CEGF的形状是；

② $\frac{A G}{B E}$ 的值为；

(2)、（探究与证明）
在图1的基础上，将正方形CEGF绕点C按顺时针方向旋转α角（0°<α<45°），如图2所示，试探究线段AG与BE之间的数量关系，并说明理由；

(3)、（拓展与运用）
如图3，在（2）的条件下，正方形CEGF 在旋转过程中，当B、E、F三点共线时，探究AG和GE的位置关系，并说明理由．

查看试题解析
23. 在平面直角坐标系中，正方形 $A_{1} B_{1} C_{1} O_{1} ， A_{2} B_{2} C_{2} C_{1} ， A_{3} B_{3} C_{3} C_{2}$ .... 按如图的方式放置．点 $A_{1} ， A_{2} ， A_{3}$ $⋯ A_{n}$ 和点 $C_{1} 、 C_{2} 、 C_{3} . . . . C_{n}$ 分别落在直线 $y = - x - 1$ 和 $x$ 轴上．抛物线 $L_{1}$ 过点 $A_{1} ， B_{1}$ ，且顶点在直线 $y = - x - 1$ 上，抛物线 $L_{2}$ 过点 $A_{2} 、 B_{2}$ ，且顶点在直线 $y = - x - 1$ 上，...按此规律，抛物线 $L_{n}$ ，过点 $A_{n} ， B_{n}$ ，且顶点也在直线 $y = - x - 1$ 上，其中抛物线 $L_{2}$ 交正方形 $A_{1} B_{1} C_{1} O$ 的边 $A_{1} B_{1}$ 于点 $D_{1}$ ，抛物线 $L_{3}$ 交正方形 $A_{2} B_{2} C_{2} C_{1}$ 的边 $A_{2} B_{2}$ 于点 $D_{2}$ (其中 $n \geq 1$ 且 $n$ 为正整数) ．

(1)、直接写出下列点的坐标： $B_{1}$ ， $B_{2}$ ；

(2)、写出抛物线 $L_{2} ， L_{3}$ 的解析式，并写出抛物线 $L_{2}$ 的解析式求解过程，再猜想抛物线 $L_{n}$ 的顶点坐标；

(3)、设 $\frac{A_{1} D_{1}}{D_{1} B_{1}} = k_{1} ， \frac{A_{2} D_{2}}{D_{2} B_{2}} = k_{2}$ ，试判断 $k_{1}$ 与 $k_{2}$ 的数量关系并说明理由．

查看试题解析