江西省2022年初中学业水平考试数学模拟试题
试卷更新日期：2022-04-15 类型：中考模拟
一、单选题
-
1. 2022的相反数是（ ）A、﹣2022 B、2022 C、 D、﹣2. 下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
3. 某种球形病毒的直径为0.000000 43米，将数据0.000 000 43用科学记数法表示为（ ）A、 B、 C、 D、4. 某工厂为了解工人加工某工件的情况，随机抽取了部分工人一天加工该工件的个数进行了统计，统计数据如表所示，则被抽取的工人一天加工该工件的中位数和众数分别是（ ）一天加工该工件的个数（个）
70
80
90
100
110
工人人数
4
11
10
8
7
A、90，80 B、90，90 C、95，90 D、95，805. 斐波那契螺旋线，也称“黄金螺旋线”，它可以通过分别以1，1，2，3，5，…为半径，依次作圆心角为90°的扇形弧线画出来(如图)．第1步中扇形的半径是1 cm，按如图所示的方法依次画，则第6步所画扇形的弧长为（ ）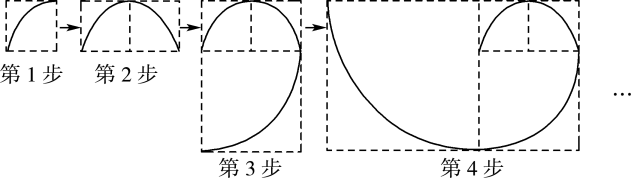
A、π B、4π C、π D、π6. 如图，在平面直角坐标系中，M、N、C三点的坐标分别为（ ，1），（3，1），（3，0），点A为线段MN上的一个动点，连接AC，过点A作 交y轴于点B，当点A从M运动到N时，点B随之运动，设点B的坐标为（0，b），则b的取值范围是（ ）
A、 B、 C、 D、二、填空题
-
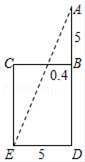
7. 已知x＝－1，则|x－5|＝ ．8. 函数 中，自变量x的取值范围是 ．9. “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为尺．
10. 观察下列一行数：4，1，－8，1，16，1，－32，1，64，1，－128，1，…则第19个数与第20个数的和为 ．11. 如图，在Rt ABC中，∠BAC＝90°，AD⊥BC，垂足为点D，线段AE与线段CD相交于点F，且AE＝AB，连接DE，∠E＝∠C，若AD＝3DE，则cosE的值为.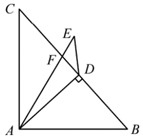
12. 如图，在矩形ABCD中，AB＝3，AD＝4，E、F分别边BC、CD上一点，EF⊥AE，将△ECF沿EF翻折得△EC′F，连接AC′，当BE＝时，△AEC′是以AE为腰的等腰三角形．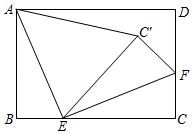
三、解答题
-
13.(1)、解方程：－＝1；(2)、解不等式组： 并将解集表示在数轴上．
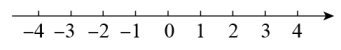14. 先化简，再求代数式 的值，其中15. 某超市的奶制品专柜有A、B、C、D四个品牌进行促销活动，每个品牌均有六个种类的奶制品：1.纯牛奶，2.酸奶，3.核桃奶，4.花生奶，5.红枣奶，6.草莓奶.活动规则如下：每位参与活动的顾客先从标有A、B、C、D的四支签里随机抽取一支，记下字母放回，所抽字母即代表所选品牌.抽完签的顾客再掷一枚质地均匀的骰子一次，向上一面的点数即代表所选奶制品的种类.参与活动的顾客均可免费获得一箱所选品牌及种类的奶制品.(1)、若某天参加活动的顾客有150人次，超市发放A品牌奶制品39箱，求这天参加此次活动得到A品牌奶制品的频率；(2)、若王阿姨参与了此次活动，且她喜欢B品牌的核桃奶，请你用树状图或列表的方法，求王阿姨免费获得一箱B品牌的核桃奶的概率.16. 已知BC是⊙O的直径，△ABC为等腰三角形，请仅用无刻度的直尺完成下列作图．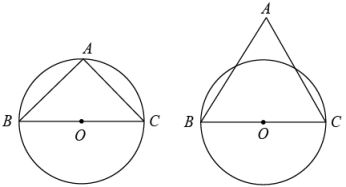
图1 图2
(1)、在图1中画出菱形ABDC；(2)、在图2中画出菱形ABDC.17. 本学期学校开展以“感受中华传统美德”为主题的研学活动，组织150名学生参观历史博物馆和民俗展览馆，每一名学生只能参加其中一项活动，共支付票款2000元，票价信息如下：地点
票价
历史博物馆
10元 人
民俗展览馆
20元 人
(1)、请问参观历史博物馆和民俗展览馆的人数各是多少人？(2)、若学生都去参观历史博物馆，则能节省票款多少元？18. 如图，在直角坐标系中，已知点 (4，0)，等边三角形 的顶点 在反比例函数 的图象上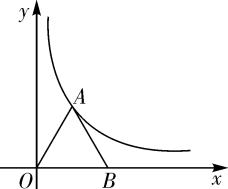
(1)、求反比例函数的表达式．(2)、把△ 向右平移 个单位长度，对应得到△ ，当这个函数图象经过△ 一边的中点时，求 的值．
19. 某校计划组织学生参加“书法”、“摄影”、“航模”、“围棋”四个课外兴题小组.要求每人必须参加.并且只能选择其中一个小组，为了解学生对四个课外兴趣小组的选择情况，学校从全体学生中随机抽取部分学生进行问卷调查，并把调查结果制成如图所示的扇形统计图和条形统计图(部分信息未给出).请你根据给出的信息解答下列问题：
(1)、求参加这次问卷调查的学生人数.并补全条形统计图(画图后请标注相应的数据)；(2)、m= ， n=；(3)、若某校共有1200名学生，试估计该校选择“围棋”课外兴趣小组有多少人？20. 如图1是一扇门打开后的情景示意图，图2为底面BEB′的平面示意图，其中门的宽度AB＝1 m，EA⊥EB′，A到墙角E的距离AE＝0.5 m．设点E，A，B在一条直线上，门打开后被与门所在墙面垂直的墙阻挡，边BC靠在墙B′C′的位置．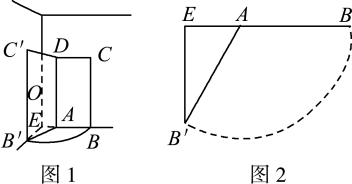
(1)、求∠EAB′的度数；(2)、打开门后，门边上的点B在地面扫过的痕迹为 ， 求与墙角EB，EB′围成区域的面积 (结果精确到0.1 m2；参考数据：π≈3.14，≈1.73)21. 如图，已知∠MON＝90°，OT是∠MON的平分线，A是射线OM上一点，OA＝8cm.动点P从点A出发，以1cm/s的速度沿AO水平向左作匀速运动，与此同时，动点Q从点O出发，也以1cm/s的速度沿ON竖直向上作匀速运动.连接PQ，交OT于点B.经过O、P、Q三点作圆，交OT于点C，连接PC、QC.设运动时间为t（s），其中0＜t＜8.
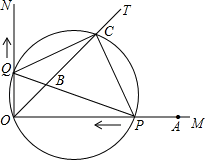(1)、求OP+OQ的值；(2)、是否存在实数t，使得线段OB的长度最大？若存在，求出t的值；若不存在，说明理由.(3)、求四边形OPCQ的面积.22. 在平面直角坐标系中，点A是抛物线y＝－x2＋mx＋2m＋2与y轴的交点，点B在该抛物线上，将该抛物线A，B两点之间(包括A，B两点)的部分记为图象G，设点B的横坐标为2m－1．(1)、当m＝1时，①图象G对应的函数y的值随x的增大而 ▲ (填“增大”或“减小”)，自变量x的取值范围为 ▲ ；
②求图象G最高点的坐标．
(2)、当m<0时，若图象G与x轴只有一个交点，求m的取值范围．(3)、设图象G的最高点与最低点的纵坐标之差为h，求h与m之间的函数关系式．23. 定义：有一组邻角相等，对角线相等，且对边不相等的凸四边形叫做“等邻对角四边形”，如图1，在四边形中， ， 四边形即为“等邻对角四边形”．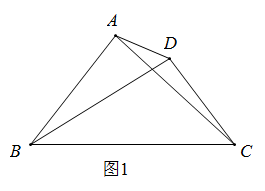
(1)、概念理解
①如图2，在等边中， ， 点D，E分别在上， ， 当的长为时，四边形为“等邻对角四边形”．
②如图3，在中，点E，D在上，点F在上， ， 四边形为“等邻对角四边形”，若 ， 则的度数为 ．
(2)、性质探究根据图1及其条件，探究与的数量关系．
(3)、问题解决如图4，在“等邻对角四边形”中，与的延长线相交于点E．若 ， 求的长，并指出的度数是否可以等于90°，不必说明理由．