江西省赣州市瑞金市2022年九年级下学期中考模拟数学试题
试卷更新日期:2022-04-15 类型:中考模拟
一、单选题
-
1. -3的相反数是( )A、 -3 B、 C、 D、2. 下列计算或运算中,正确的是 ( )A、a6÷a2=a3 B、(-2a2)3=-8a8 C、(a-3)(3+a)=a2-9 D、(a-b)2=a2-b23. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,直线a∥b,c、d是截线且交于点A,若∠1 = 55°,∠2 = 100 °,则∠A=( )
4. 如图,直线a∥b,c、d是截线且交于点A,若∠1 = 55°,∠2 = 100 °,则∠A=( )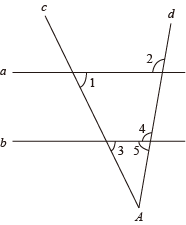 A、40° B、45° C、55° D、65°5. 如图,是的直径,弦 , 垂足为 , , , 则等于( )
A、40° B、45° C、55° D、65°5. 如图,是的直径,弦 , 垂足为 , , , 则等于( ) A、 B、 C、 D、6. 如图,将边长为的正方形绕点B逆时针旋转30°,那么图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,将边长为的正方形绕点B逆时针旋转30°,那么图中阴影部分的面积为( ) A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
7. 使式子有意义的x的取值范围是 .8. 因式分解: .9. 随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系.去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为 .10. 等腰三角形三边长分别为 ,且 是关于 的一元二次方程 的两根,则 的值为11. 如图,直线AB,AD与⊙O分别相切于点B、D两点,C为⊙O上一点,且∠BCD=140°,则∠A的度数是
 12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:①2a﹣b=0; ②abc>0 ③4ac﹣b2<0; ④9a+3b+c<0; ⑤8a+c<0. 其中正确的结论有
12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:①2a﹣b=0; ②abc>0 ③4ac﹣b2<0; ④9a+3b+c<0; ⑤8a+c<0. 其中正确的结论有
三、解答题
-
13.(1)、计算:(2)、化简:14. 如图点E,F分别是矩形ABCD的边AD,AB上一点,若AE=DC=2ED,且EF⊥EC
 (1)、求证:点F为AB的中点.(2)、延长EF与CB的延长线相交于点H,连接AH,已知ED=2,求AH的值.15. 先化简: , 然后,m在1,2,3中选择一个合适的数代入求值.16. 按要求作图,不要求写作法,但要保留作图痕迹
(1)、求证:点F为AB的中点.(2)、延长EF与CB的延长线相交于点H,连接AH,已知ED=2,求AH的值.15. 先化简: , 然后,m在1,2,3中选择一个合适的数代入求值.16. 按要求作图,不要求写作法,但要保留作图痕迹我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
 (1)、如图2,在▱ABCD中,E为CD的中点,作BC的中点F;(2)、图3,在由小正方形组成的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH17. 某校准备从八年级1班、2班的团员中选取两名同学作为运动会的志愿者,已知1班有4名团员(其中男生2人,女生2人).2班有3名团员(其中男生1人,女生2人).(1)、如果从这两个班的全体团员中随机选取一名同学作为志愿者的组长,则这名同学是男生的概率为;(2)、如果分别从1班、2班的团员中随机各选取一人,请用画树状图或列表的方法求这两名同学恰好是一名男生、一名女生的概率.18. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.
(1)、如图2,在▱ABCD中,E为CD的中点,作BC的中点F;(2)、图3,在由小正方形组成的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH17. 某校准备从八年级1班、2班的团员中选取两名同学作为运动会的志愿者,已知1班有4名团员(其中男生2人,女生2人).2班有3名团员(其中男生1人,女生2人).(1)、如果从这两个班的全体团员中随机选取一名同学作为志愿者的组长,则这名同学是男生的概率为;(2)、如果分别从1班、2班的团员中随机各选取一人,请用画树状图或列表的方法求这两名同学恰好是一名男生、一名女生的概率.18. 家庭过期药品属于“国家危险废物”,处理不当将污染环境,危害健康.某校学生杨杨和舟舟为了解市民家庭处理过期药品的方式,决定对全市家庭作一次简单随机抽样调查.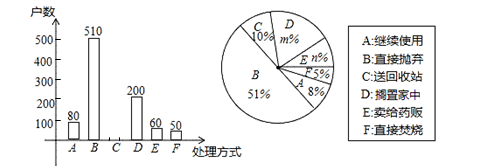 (1)、下列选取样本的方法最合理的一种是 . (只需填上符合题意答案的序号)
(1)、下列选取样本的方法最合理的一种是 . (只需填上符合题意答案的序号)①在市中心某个居民区以家庭为单位随机抽取;
②在全市医务工作者中以家庭为单位随机抽取;
③在全市常住人口中以家庭为单位随机抽取.
(2)、本次抽样调查发现,接受调查的家庭都有过期药品,现将有关数据呈现如图:①m= ▲ ;n= ▲ ;
②补全条形统计图;
③根据调查数据,你认为该市市民家庭处理过期药品最常见的方式是 ▲ ;
④家庭过期药品的正确处理方式是送回收站点,若该市有180万户家庭,请估计大约有多少户家庭处理过期药品的方式是送回收站点.
19. 如图,在平面直角坐标系中,直线()与双曲线()交于A、B两点,已知点A(m,2),点B(-1,-4).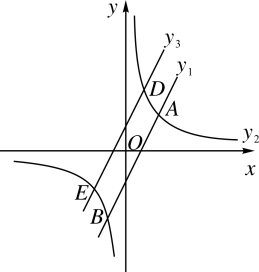 (1)、求直线和双曲线的解析式;(2)、把直线y1沿x轴负方向平移2个单位后得到直线 y3 ,直线y3与双曲线y2交于D、E两点,当y2>y3时,求x 的取值范围.20. 如图所示的是一款机械手臂,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图1所示,经测量,上臂 , 中臂 , 底座
(1)、求直线和双曲线的解析式;(2)、把直线y1沿x轴负方向平移2个单位后得到直线 y3 ,直线y3与双曲线y2交于D、E两点,当y2>y3时,求x 的取值范围.20. 如图所示的是一款机械手臂,由上臂、中臂和底座三部分组成,其中上臂和中臂可自由转动,底座与水平地面垂直.在实际运用中要求三部分始终处于同一平面内,其示意图如图1所示,经测量,上臂 , 中臂 , 底座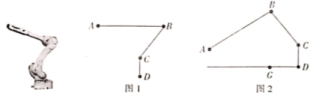 (1)、若上臂与水平面平行, . 计算点到地面的距离.(2)、在一次操作中,中臂与底座成夹角,上臂与中臂夹角为 , 如图2,计算这时点到地面的距离.与图1状态相比,这时点A向前伸长了多少?21. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)、若上臂与水平面平行, . 计算点到地面的距离.(2)、在一次操作中,中臂与底座成夹角,上臂与中臂夹角为 , 如图2,计算这时点到地面的距离.与图1状态相比,这时点A向前伸长了多少?21. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.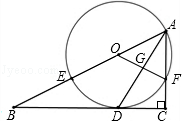 (1)、求证:BC是⊙O的切线;(2)、设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;(3)、若BE=8,sinB= ,求DG的长,22. 如图,在等腰三角形ABC中,∠BAC=90°,点A在x轴上,点B在y轴上,点C(3,1),二次函数y=x2+bx-的图象经过点C.
(1)、求证:BC是⊙O的切线;(2)、设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;(3)、若BE=8,sinB= ,求DG的长,22. 如图,在等腰三角形ABC中,∠BAC=90°,点A在x轴上,点B在y轴上,点C(3,1),二次函数y=x2+bx-的图象经过点C. (1)、求二次函数的解析式,并把解析式化成y=a(x-h)2+k的形式;(2)、把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积;(3)、在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.23. 如图,在Rt△ABC中,∠B=90°,BC=5 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)、求二次函数的解析式,并把解析式化成y=a(x-h)2+k的形式;(2)、把△ABC沿x轴正方向平移,当点B落在抛物线上时,求△ABC扫过区域的面积;(3)、在抛物线上是否存在异于点C的点P,使△ABP是以AB为直角边的等腰直角三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.23. 如图,在Rt△ABC中,∠B=90°,BC=5 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.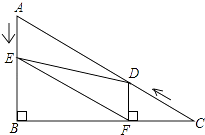 (1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)、当t为何值时,△DEF为直角三角形?请说明理由.
(1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.(3)、当t为何值时,△DEF为直角三角形?请说明理由.