内蒙古自治区兴安盟突泉县2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-15 类型:期末考试
一、单选题
-
1. 式子成立的条件是( )A、 B、 C、 D、2. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、3. 如图,△ABC中,∠ACB=90°,AD=DB,CD=4,则AB等于( )
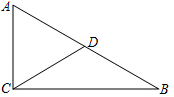 A、8 B、6 C、4 D、24. 一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知平行四边形 中, ,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )A、 B、 C、 D、6. 下列各组数中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )A、3、4、5 B、5、12、13 C、 D、7、24、257. 对于一组数据:x1 , x2 , x3 , …,x10 , 若去掉一个最大值和一个最小值,则下列统计量一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )
A、8 B、6 C、4 D、24. 一次函数y=kx+b中,y随x的增大而增大,b<0,则这个函数的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知平行四边形 中, ,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )A、 B、 C、 D、6. 下列各组数中的三个数值分别为三角形的三边长,不能构成直角三角形的是( )A、3、4、5 B、5、12、13 C、 D、7、24、257. 对于一组数据:x1 , x2 , x3 , …,x10 , 若去掉一个最大值和一个最小值,则下列统计量一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差8. 如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是( )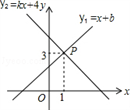 A、x>﹣2 B、x>0 C、x>1 D、x<19. 如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( )
A、x>﹣2 B、x>0 C、x>1 D、x<19. 如图,一根长5米的竹竿 斜靠在竖直的墙上,这时 为4米,若竹竿的顶端 沿墙下滑2米至 处,则竹竿底端 外移的距离 ( ) A、小于2米 B、等于2米 C、大于2米 D、以上都不对10. 如图,菱形ABCD中,BD=8,AC=6,AE⊥CD,垂足为点E,则AE的长为( )
A、小于2米 B、等于2米 C、大于2米 D、以上都不对10. 如图,菱形ABCD中,BD=8,AC=6,AE⊥CD,垂足为点E,则AE的长为( )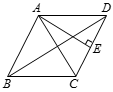 A、1.2 B、2.4 C、4.8 D、511. 小甬,小真两人的跑步路程y(米)和跑步时间x(分)之间的关系如图所示,已知小甬的跑步速度比小真快,则下列说法正确的是( )
A、1.2 B、2.4 C、4.8 D、511. 小甬,小真两人的跑步路程y(米)和跑步时间x(分)之间的关系如图所示,已知小甬的跑步速度比小真快,则下列说法正确的是( )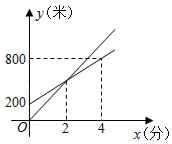 A、小甬每分钟跑200米.小真每分钟跑100米 B、小甬每跑100米时,小真只能跑60米 C、相遇时,小甬、小真两人都跑了500米 D、经过4分钟时,小甬、小真两人都跑800米12. 如图,在中,点、分别是、的中点,平分 , 交于点 , 若 , 则的长是( )
A、小甬每分钟跑200米.小真每分钟跑100米 B、小甬每跑100米时,小真只能跑60米 C、相遇时,小甬、小真两人都跑了500米 D、经过4分钟时,小甬、小真两人都跑800米12. 如图,在中,点、分别是、的中点,平分 , 交于点 , 若 , 则的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若一个正方形的面积为 , 则它的边长可表示为 .14. 将直线向下平移3个单位得到的直线为 .15. 一组数据:1,2,3,4,5,a的众数是3,则这组数据的方差是 .16. 如图,在正方形的外侧作等边 , 、相交于点 , 则为度.
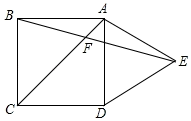 17. 如图,折叠矩形纸片的一边 , 使点落在边上的点处,BC=10cm,AB=8cm,则的长为 .
17. 如图,折叠矩形纸片的一边 , 使点落在边上的点处,BC=10cm,AB=8cm,则的长为 .
三、解答题
-
18. .19. .20. 如图,在四边形ABCD中,AB=13,BC=3,CD=4,DA=12,∠ADB=90°,求四边形ABCD的面积.
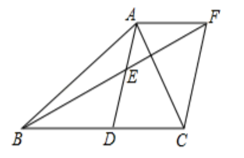
 21. 已知一次函数 的图像经过点A(-1,1),B(2,0)两点,且与y轴交于点C.(1)、求一次函数的解析式,(2)、求三角形AOC的面积22. 如图,四边形是一个正方形, . 分别在、边上,且 . 、交于点.请说出线段和的数量关系和位置关系,并证明你的结论.
21. 已知一次函数 的图像经过点A(-1,1),B(2,0)两点,且与y轴交于点C.(1)、求一次函数的解析式,(2)、求三角形AOC的面积22. 如图,四边形是一个正方形, . 分别在、边上,且 . 、交于点.请说出线段和的数量关系和位置关系,并证明你的结论.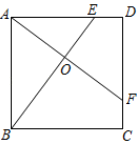 23. 青岛市某实验中学举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分.
23. 青岛市某实验中学举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分.方案1:所有评委所给分的平均数.
方案2:在所有评委所给分中去掉一个最高分和一个最低分,然后再计算其余评委所给分的平均数.
方案3:所有评委所给分的中位数.
方案4:所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计试验,如图所示的是这个同学的得分统计图.
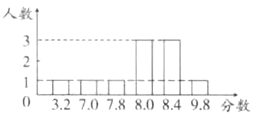 (1)、分别按上述4个方案计算这个同学演讲的最后得分;(2)、根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
(1)、分别按上述4个方案计算这个同学演讲的最后得分;(2)、根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.