内蒙古自治区呼伦贝尔市满洲里市2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-15 类型:期末考试
一、单选题
-
1. 在实数 , 0, , , 1.4141中,无理数有( )A、4个 B、3个 C、2个 D、1个2. 下列各组数,互为相反数的是( )A、﹣2与 B、|﹣ |与 C、﹣2与(﹣ )2 D、2与3. 若a>b,则下列不等式一定成立的是( )A、a+3<b+3 B、﹣2a<﹣2b C、 D、a2<b24. 下列图形中,不能通过其中一个四边形平移得到的是( )A、
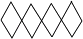 B、
B、 C、
C、 D、
D、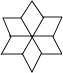 5. 当前,“低头族”已成为热门话题之一,小颖为了解路边行人步行边低头看手机的情况,她应采用的收集数据的方式是( )A、对学校的同学发放问卷进行调查 B、对在路边行走的学生随机发放问卷进行调查 C、对在路边行走的行人随机发放问卷进行调查 D、对在图书馆里看书的人发放问卷进行调查6. 如图所示,AC⊥BC与C,CD⊥AB于D,图中能表示点到直线(或线段)的距离的线段有( )
5. 当前,“低头族”已成为热门话题之一,小颖为了解路边行人步行边低头看手机的情况,她应采用的收集数据的方式是( )A、对学校的同学发放问卷进行调查 B、对在路边行走的学生随机发放问卷进行调查 C、对在路边行走的行人随机发放问卷进行调查 D、对在图书馆里看书的人发放问卷进行调查6. 如图所示,AC⊥BC与C,CD⊥AB于D,图中能表示点到直线(或线段)的距离的线段有( ) A、1条 B、2条 C、3条 D、5条7. 已知点P(m﹣1,m+2)在x轴上,那么P点的坐标为( )A、(﹣3,0) B、(3,0) C、(0,3) D、(0,﹣3)8. 已知方程组 , 则的值为( )A、4 B、5 C、3 D、69. 某市为了解870万市民的出行情况,科学规划轨道交通,500名志愿者走入1万户家庭,发放了4万份问卷,进行调查登记.该调查中的样本容量是( )A、870万 B、500 C、1万 D、4万10. 点P坐标为(m+1,m-2),则点P不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 如果不等式组有解,则m的取值范围( )A、m<﹣1 B、m>﹣1 C、m≤﹣1 D、m≥﹣112. 在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元购买A,B两种奖品(两种都要买),A种每个15元,B种每个25元,在钱全部用完的情况下,购买方案共有( )A、2种 B、3种 C、4种 D、5种
A、1条 B、2条 C、3条 D、5条7. 已知点P(m﹣1,m+2)在x轴上,那么P点的坐标为( )A、(﹣3,0) B、(3,0) C、(0,3) D、(0,﹣3)8. 已知方程组 , 则的值为( )A、4 B、5 C、3 D、69. 某市为了解870万市民的出行情况,科学规划轨道交通,500名志愿者走入1万户家庭,发放了4万份问卷,进行调查登记.该调查中的样本容量是( )A、870万 B、500 C、1万 D、4万10. 点P坐标为(m+1,m-2),则点P不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限11. 如果不等式组有解,则m的取值范围( )A、m<﹣1 B、m>﹣1 C、m≤﹣1 D、m≥﹣112. 在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元购买A,B两种奖品(两种都要买),A种每个15元,B种每个25元,在钱全部用完的情况下,购买方案共有( )A、2种 B、3种 C、4种 D、5种二、填空题
-
13. 如图,已知AD//BC , BD平分∠ABC , ∠A=112°,且BD⊥CD , 则∠ADC= .
 14. 化简 = .15. 已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.16. 如图,下列结论:① 与 是内错角;② 与 是同位角;③ 与 是同旁内角;④ 与 不是同旁内角,其中正确的是(只填序号).
14. 化简 = .15. 已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为.16. 如图,下列结论:① 与 是内错角;② 与 是同位角;③ 与 是同旁内角;④ 与 不是同旁内角,其中正确的是(只填序号).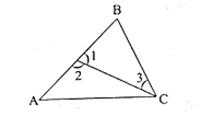 17. 如果方程组的解为 , 那么“*”表示的数是.
17. 如果方程组的解为 , 那么“*”表示的数是.三、解答题
-
18. 已知m﹣15的平方根是±2, , 求m+n的算术平方根.19. 解方程组: .20. 解不等式组 , 并在数轴上画出该不等式组的解集.
 21. 完成下面推理过程.在括号内的横线上填上推理依据.
21. 完成下面推理过程.在括号内的横线上填上推理依据.如图,已知:ABEF,EP⊥EQ,∠EQC+∠APE=90°,求证:ABCD

证明:∵ABEF
∴∠APE= ▲ ( ▲ )
∵EP⊥EQ
∴∠PEQ= ▲ (垂直的定义)
即∠QEF+∠PEF=90°
∴∠APE+∠QEF=90°
又∵∠EQC+∠APE=90°
∴∠EQC= ▲ ( ▲ )
∴EFCD( ▲ )
∴ABCD( ▲ )
22. 阅读下面的文字,解答问题.大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,但是由于12,所以的整数部分为1.将减去其整数部分1,差就是小数部分 . 根据以上的内容,解答下面的问题:
(1)、的整数部分是 ,小数部分是;(2)、若设(2)整数部分是x,小数部分是y,分别求出x与y的值.23. 某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和频数分布直方图,如图:次数
频数
60≤x<80
80≤x<100
4
100≤x<120
18
120≤x<140
13
140≤x<160
8
160≤x<180
180≤x<200
1
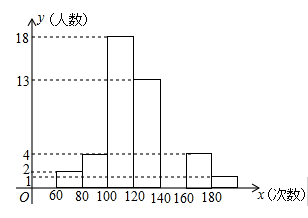 (1)、补全频数分布表和频数分布直方图;(2)、样本数据中组距是 , 组数是 ;(3)、若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?24. 甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?25. 一工厂以90元/每箱的价格购进100箱原材料,准备由甲、乙两个车间全部用于生产某种产品,甲车间用每箱原材料可生产出该产品12千克,乙车间用每箱原材料可生产出的该产品比甲车间少2千克,已知该产品的售价为40元/千克,生产的产品全部售出,那么原材料最少分配给甲车间多少箱,才能使去除成本后所获得的总利润不少于35000元?26. 在平面直角坐标系中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(﹣3,﹣1),点N的坐标为(3,﹣2).
(1)、补全频数分布表和频数分布直方图;(2)、样本数据中组距是 , 组数是 ;(3)、若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?24. 甲、乙两人相距50千米,若同向而行,乙10小时追上甲;若相向而行,2小时两人相遇.求甲、乙两人每小时各行多少千米?25. 一工厂以90元/每箱的价格购进100箱原材料,准备由甲、乙两个车间全部用于生产某种产品,甲车间用每箱原材料可生产出该产品12千克,乙车间用每箱原材料可生产出的该产品比甲车间少2千克,已知该产品的售价为40元/千克,生产的产品全部售出,那么原材料最少分配给甲车间多少箱,才能使去除成本后所获得的总利润不少于35000元?26. 在平面直角坐标系中,点A的坐标为(0,4),线段MN的位置如图所示,其中点M的坐标为(﹣3,﹣1),点N的坐标为(3,﹣2). (1)、将线段MN平移得到线段AB,其中点M的对应点为A,点N的对应点为B.点M平移到点A的过程可以是:先向平移个单位长度,再向平移个单位长度;(2)、在(1)的条件下,若点C的坐标为(4,0),连接AC,BC,求ABC的面积;(3)、在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为 , 若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、将线段MN平移得到线段AB,其中点M的对应点为A,点N的对应点为B.点M平移到点A的过程可以是:先向平移个单位长度,再向平移个单位长度;(2)、在(1)的条件下,若点C的坐标为(4,0),连接AC,BC,求ABC的面积;(3)、在y轴上是否存在点P,使以A、B、P三点为顶点的三角形的面积为 , 若存在,请直接写出点P的坐标;若不存在,请说明理由.