内蒙古自治区呼伦贝尔市额尔古纳市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $\sqrt{16}$ ， ﹣3.141， $\frac{π}{2}$ ， ﹣0.5， $\sqrt{2}$ ， 0.5858858885…， $\frac{22}{7}$ 中无理数有（）个．

A、3 B、4 C、5 D、6

查看试题解析
2. 下列计算中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt[3]{8} = \pm 2$ C、 $- \sqrt{{(- 3)}^{2}} = 3$ D、 $| 1 - \sqrt{2} | = \sqrt{2} - 1$

查看试题解析
3. 在下列调查中，宜采用全面调查的是（）

A、了解某区中小学生视力情况 B、了解某市百岁以上老人的健康情况 C、了解一批灯泡的使用寿命 D、了解老年人对预防新冠状病毒知识的掌握

查看试题解析
4. 下列图形中，能由 $∠ 1 = ∠ 2$ 得到 $A B / / C D$ 的是（）

A、 B、 C、 D、

查看试题解析
5. 已知 $P (x ， y)$ 在第二象限，则 $Q (- x + 1 ， - y - 2)$ 在第几象限 $($ 　　 $)$

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 若a＞b，则（）

A、a＋c＞b﹣c B、a|m|＞b|m| C、a﹣1＞b D、 $\frac{a}{1 + n^{2}} > \frac{b}{1 + n^{2}}$

查看试题解析
7. 为积极响应南充市创建“全国卫生城市”的号召，某校1500名学生参加了卫生知识竞赛，成绩记为A，B，C，D四等.从中随机抽取了部分学生成绩进行统计，绘制成如图所示的两幅不完整的统计图，根据图中信息，以下说法不正确的是（）

A、样本容量是200 B、D等所在扇形的圆心角为15° C、样本中C等所占百分比是10％ D、估计全校学生成绩为A等的大约有900人

查看试题解析
8. 象棋在中国有着三千多年的历史，如图是一方的棋盘，如果“帅”的坐标是（0，1），“卒”的坐标是（2，2），那么“马”的坐标是（）

A、（﹣2，1） B、（2，﹣2） C、（﹣2，2） D、（2，2）

查看试题解析
9. 若关于x的方程x﹣2+3k= $\frac{x + k}{3}$ 的解是正数，则k的取值范围是（）

A、k＞ $\frac{3}{4}$ B、k≥ $\frac{3}{4}$ C、k＜ $\frac{3}{4}$ D、k≤ $\frac{3}{4}$

查看试题解析
10. 如图，直线AB、CD交于点O，OT⊥AB于O，CE∥AB交CD于点C，若∠ECO＝30°，则∠DOT等于（）

A、30° B、45° C、60° D、120°

查看试题解析
11. 《九章算术》是我国古代数学的经典著作，其中记载了一道有趣的数学问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问：金、银一枚各重几何？”意思是：甲袋中有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同）称重两袋相等，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（）

A、 ${\begin{cases} x = 9 y \\ (10 y + x) - (8 x + y) = 13 \end{cases}$ B、 ${\begin{cases} 11 x = 9 y \\ (8 x + y) - (10 y + x) = 13 \end{cases}$ C、 ${\begin{cases} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{cases}$ D、 ${\begin{cases} 9 x = 11 y \\ (8 x + y) - (10 y + x) = 12 \end{cases}$

查看试题解析
12. 关于x的不等式组 ${\begin{matrix} 3 x - 1 > 4 (x - 1) \\ x < m \end{matrix}$ 的解集为x＜3，那么m的取值范围为（）

A、m=3 B、m＞3 C、m＜3 D、m≥3

查看试题解析

二、填空题

13. $\sqrt{16}$ 的平方根是．

查看试题解析
14. 已知Q（2x﹣4，x²﹣1）在x轴上，则点Q的坐标为 .

查看试题解析
15. 一家电脑生产厂家在某城市三个经销本厂产品的大商场调查，产品的销量占这三个大商场同类产品销量的40%，由此在广告中宣传，他们的产品在国内同类产品的销售量占40%．请你根据所学的统计知识，判断该宣传中的数据是否可靠：，理由是．

查看试题解析
16. 已知三条不同的直线a、b、c在同一平面内，下列四条命题：
①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．其中假命题的是．（填写序号）

查看试题解析
17. 若方程组 ${\begin{array}{l} 3 x - y = 4 k - 5 \\ 2 x + 6 y = k \end{array}$ 的解中 $x + y = 16$ ，则k等于；

查看试题解析
18. 小明将两把直尺按图所示叠放，使其中一把直尺的一个顶点恰好落在另一把直尺的边上，则∠1＋∠2＝度．

查看试题解析

三、解答题

19.

(1)、 $\sqrt{(- 5)^{2}} - | \sqrt{2} - 2 | + \sqrt[3]{- 27} + 3 \sqrt{2}$ ．

(2)、已知2a﹣1的算术平方根是3，3a＋b﹣9的立方根是2，c是 $\sqrt{17}$ 的整数部分，求a＋2b＋c的值．

查看试题解析
20.

(1)、已知 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$ 是关于x，y的二元一次方程组 ${\begin{array}{l} a x + b y = 4 \\ a x - b y = - 2 \end{array}$ 的解，求b﹣4a的立方根．

(2)、解不等式组 ${\begin{array}{l} 5 x - 6 \leq 2 (x + 3) \\ \frac{x}{4} - 1 < \frac{x - 3}{3} \end{array}$ ，把解集表示在数轴上，并写出其整数解．

查看试题解析
21. 为了进一步了解某校八年级学生的身体素质情况，体育老师抽测了该校八年级（1）班50名学生一分钟的跳绳次数，以测试数据为样本，绘制出部分频数分布表和部分频数分布直方图，图表如下所示：请结合图表完成下列问题：
组别
次数x
频数（人数）
第1组
80≤x＜100
6
第2组
100≤x＜120
8
第3组
120≤x＜140
a
第4组
140≤x＜160
18
第5组
160≤x＜180
6

(1)、本次调查为（填全面调查或抽样调查），样本为；样本容量为；

(2)、a＝；观察已绘制的部分频数分布直方图，组距为；

(3)、请把频数分布直方图补充完整；

(4)、若在一分钟内跳绳次数少于120次的为测试不合格，则该校八年级共1000人中，一分钟跳绳不合格的人数大约有多少？

查看试题解析
22. 如图，在正方形网格中，横、纵坐标均为整数的点叫做格点，点A、B、C、O均在格点上，其中O为坐标原点，A（﹣3，3）．

(1)、将△ABC向右平移6个单位，向下平移1个单位，对应得到△A₁B₁C₁ ，请在图中画出平移后的△A₁B₁C₁ ，若△ABC内部一点M的坐标为（a，b），写出点M的对应点M₁的坐标；

(2)、求△A₁B₁C₁的面积；

(3)、在x轴上有一点P，使得△PA₁B₁的面积等于△A₁B₁C₁的面积，直接写出点P坐标．

查看试题解析
23. 如图所示，已知∠DAB=∠DCB，AF平分∠DAB，CE平分∠DCB，∠FCE=∠CEB，试说明：AF∥CE．
解：因为∠DAB=∠DCB（                  ▲                  ），
又AF平分∠DAB，
所以                  ▲                  = $\frac{1}{2}$ ∠DAB（                  ▲                  ），
又因为CE平分∠DCB，
所以∠FCE=                  ▲                  （                  ▲                  ），
所以∠FAE=∠FCE．
因为∠FCE=∠CEB，
所以                  ▲                  =                  ▲
所以AF∥CE（                  ▲                  ）

查看试题解析
24. 如图，已知∠A＝∠C，AD⊥BE于点F，BC⊥BE于点B，点E，D，C在同一条直线上．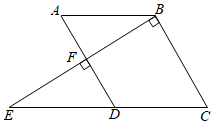

(1)、判断AB与CD的位置关系，并说明理由．

(2)、若∠ABC＝130°，求∠BEC的度数．

查看试题解析
25. 第24届冬季奥林匹克运动会将于2022年02月04日至2022年02月20日在中华人民共和国北京市和张家口市联合举行，这是中国历史上第一次举办冬季奥运会．冬奥会吉祥物“冰墩墩”和“雪容融”陶制品分为小套装和大套装两种．已知购买2个小套装比购买1个大套装少用20元；购买3个小套装和2个大套装，共需390元．

(1)、求这两种套装的单价分别为多少元？

(2)、太原市某校计划用不多于1500元的资金购买这种陶制品小套装和大套装共20个作为奖品，则该校最多可以购买大套装多少个？

查看试题解析

组别	次数x	频数（人数）
第1组	80≤x＜100	6
第2组	100≤x＜120	8
第3组	120≤x＜140	a
第4组	140≤x＜160	18
第5组	160≤x＜180	6