内蒙古自治区呼和浩特市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. 16的算术平方根是（）

A、8 B、-8 C、4 D、 $\pm 4$

查看试题解析
2. 下列方程组中是二元一次方程组的是（）

A、 ${\begin{array}{l} \frac{2}{x} - y = 4 \\ 2 x + y = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4 \\ 2 x + y = 3 \end{array}$ C、 ${\begin{array}{l} 2 x - y = 5 \\ 2 y + z = 1 \end{array}$ D、 ${\begin{array}{l} x + y = 5 \\ x^{2} + y^{2} = 12 \end{array}$

查看试题解析
3. 下列命题中是真命题的是（）

A、﹣2是4的一个平方根 B、两条直线被第三条直线所截，同位角相等 C、 $\sqrt[3]{64}$ 的值为8 D、若a＞b，则﹣a＞﹣b

查看试题解析
4. 若点 $M (3 - m ， m - 2)$ 在第二象限，则 $m$ 的取值范围是（）

A、 $2 < m < 3$ B、 $m < 2$ C、 $m > 3$ D、 $m > 2$

查看试题解析
5. 近年来，计算步数的软件悄然兴起，每天监测自己的行走步数已成为当代人的一种习惯．某机构调查了某小区部分居民当天行走的步数（单位：千步），并将数据整理绘制成如下不完整的频数直方图和扇形统计图．
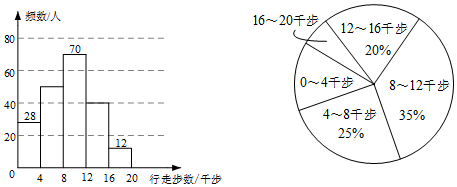
根据统计图，得出下面四个结论，其中不正确的是（）

A、此次一共调查了200位小区居民 B、行走步数为8~12千步的人数超过调查总人数的一半 C、行走步数为12~16千步的人数为40人 D、扇形图中，表示行走步数为4~8千步的扇形圆心角是 $90 °$

查看试题解析
6. 《九章算术》中的问题：“五只雀，六只燕，共重1斤（古代1斤=16两），雀重燕轻，互换其中一只，恰好一样重，问：每只雀，燕的重量各为多少两？现有列方程求解，设未知数后，小明列出其中一个方程为 $4 x + y = 5 y + x$ ，则另一个方程应为（）

A、 $6 x + 5 y = 16$ B、 $5 x + 6 y = 16$ C、 $4 y + x = 5 x + y$ D、 $x + y = 16$

查看试题解析
7. 如图所示，长方形ABCD中，点E在CD边上，AE，BE与线段FG相交构成∠ $α$ ， ∠ $β$ ，则∠1，∠2，∠ $α$ ， ∠ $β$ 之间的关系是（）

A、∠1＋∠2＋180°＝∠ $α$ ＋∠ $β$ B、∠ $α$ ＋∠2＝∠ $β$ ＋∠1 C、∠ $α$ ＋∠ $β$ ＝2（∠1＋∠2） D、∠1＋∠2＝∠a﹣∠ $β$

查看试题解析
8. 已知关于x、y的二元一次方程ax＋b＝y，下表列出了当x分别取值时对应的y值．则关于x的不等式ax＋b＜0的解集为（）
x
…
﹣2
﹣1
0
1
2
3
…
y
…
3
2
1
0
﹣1
﹣2
…

A、x＜1 B、x＞1 C、x＜0 D、x＞0

查看试题解析

二、填空题

9. “x与5的差不小于x的3倍”用不等式表示为 .

查看试题解析
10. 平面直角坐标系的应用十分广泛，用坐标表示地理位置体现了坐标系在实际生活中的应用.不管是出差办事，还是出去旅游，人民都愿意带上一副地图，它给人们出行带来了很大方便.如图是某市地图的一部分.在图中，分别以正东、正北方向为 $x$ 轴， $y$ 轴的正方向建立平面直角坐标系，若表示牡丹园的点的坐标为 $(4 ， 1)$ ，则表示狮虎园的点的坐标为.

查看试题解析
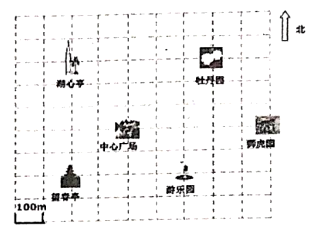11. 若方程2x＋y＝3，2x﹣my＝﹣1，3x﹣y＝2有公共解，则m的值为．

查看试题解析
12. 某学习小组为了解本城市100万成年人中大约有多少人吸烟，随机调查了50个成年人，结果其中有10个成年人吸烟，对于这个数据收集与处理的问题，有下列说法：
①该调查的方式是全面调查；
②本城市只有40个成年人不吸烟；
③本城市一定有20万人吸烟；
④样本容量是50．
其说法正确的有（填序号）．

查看试题解析
13. 已知一个角的两边与另一个角的两边互相平行，且一个角比另一个角2倍小36°，则这两个角的度数分别是．

查看试题解析
14. 已知关于x、y的二元一次方程组 ${\begin{array}{l} 2 x + y = 3 k + 1 \\ x + 2 y = 3 k - 1 \end{array}$ 的解满足x＋y＜4，则满足条件的k的最大整数为．

查看试题解析
15. 如图，下列条件中：①∠B＋∠BCD＝180°；②∠1＝∠2；③∠3＝∠4；④∠B＝∠5．能判定AB∥CD的条件为．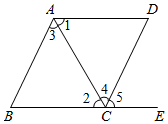

查看试题解析
16. 在平面直角坐标系中，已知A（0，a），B（b，0），其中a，b满足|a﹣2|＋（b﹣3）²＝0．点M的坐标为（ $- \frac{3}{2}$ ， 1），点N是坐标轴的负半轴上的一个动点，当四边形ABOM的面积与三角形ABN的面积相等时，此时点N的坐标为．

查看试题解析

三、解答题

17. 计算、求解

(1)、计算： $\sqrt{(- 4)^{2}} + \sqrt[3]{- 27} +$ |2 $- \sqrt{5}$ |；

(2)、解方程组： ${\begin{array}{l} y = 3 x + 1 \\ 2 x + 3 y = - 9 \end{array}$ ；

(3)、解方程组： ${\begin{array}{l} 2 x - 3 y = 1 \\ \frac{y + 1}{4} = \frac{x + 2}{3} \end{array}$ ；

(4)、解不等式组 ${\begin{array}{l} 2 x + 1 ＞ 1 x \\ x - 1 ＜ 0 \end{array}$ ，并把它的解集在数轴上表示出来．

查看试题解析
18. 已知关于x的不等式组 ${\begin{array}{l} 5 x + 1 > 3 (x - 1) ， \\ \frac{1}{2} x \leq 8 - \frac{3}{2} x + 2 a \end{array}$ 恰有两个整数解，求实数a的取值范围.

查看试题解析
19. 如图，直线AB、CD相交于点O，OM⊥AB．

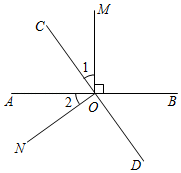(1)、若∠1＝∠2，证明：ON⊥CD；

(2)、若∠1 $= \frac{1}{3}$ ∠BOC，求∠BOD的度数．

查看试题解析
20. 小丽手中有块长方形的硬纸片，其中长比宽多10cm，长方形的周长是100cm．

(1)、求长方形的面积；

(2)、现小丽想用这块长方形的硬纸片，沿着边的方向栽出一块长与宽的比为5∶4，面积为520m²的新纸片作为他用，试判断小丽能否成功，并说明理由．

查看试题解析

21. 某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，如表是通过简单随机抽样获得的50户家庭去年的月均用水量（单位：吨），并将调查数据进行了如下整理：
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5

列频数分布表：

分组	划记	频数
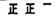
2.0＜x≤3.5		11
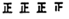
3.5＜x≤5.0		19
5.0＜x≤6.5
6.5＜x≤8.0
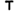
8.0＜x≤9.5		2
合计		50

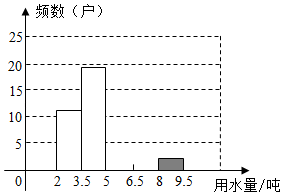(1)、把上面的频数分布表和频数分布直方图补充完整；

(2)、为了鼓励节约用水，要确定一个用水量的标准超出这个标准的部分按1.5倍价格收费，若要使60%的家庭收费不受影响，你觉得家庭月均用水量应该定为多少？为什么？

(3)、若该区有800户家庭，请你估计该区去年居民月均用水量在2.0＜x≤6.5吨范围的家庭有多少户？

查看试题解析

22. 如图，点F在线段AB上，点E，G在线段CD上，FG $//$ AE，∠1＝∠2.

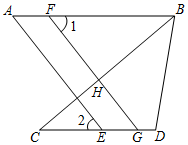(1)、求证：AB $//$ CD；

(2)、若FG⊥BC于点H，BC平分∠ABD，∠D＝100°，求∠1的度数.

查看试题解析
23. 为了培养学生的爱国主义情怀，某校学生和带队老师在5月下旬某天集体乘车去参观抗日战争纪念馆．已知学生的数量是带队老师的11倍多20人，学生和老师的总人数共536人．

(1)、请求出去参观抗日战争纪念馆学生和老师各多少人？

(2)、如果学校准备租赁A型大巴车和B型大巴车共14辆（其中B型大巴车最多有7辆），已知A型大巴车每车最多可以载35人，日租金为2000元，其中B型大巴车每车最多可以载45人，日租金为3000元，则该学校有哪几种租车方案？哪种租车方案最经济？最经济的租金是多少？

查看试题解析

x	…	﹣2	﹣1	0	1	2	3	…
y	…	3	2	1	0	﹣1	﹣2	…