内蒙古通辽市扎鲁特旗2020-2021学年七年级下学期期末考试数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）

A、 B、 C、 D、

查看试题解析
2. 点 $(5 ， - 6)$ 在第几象限（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 将点 $A (- 2 ， - 3)$ 向右平移5个单位长度，得到 $A_{1}$ ，则 $A_{1}$ 的坐标是（）

A、 $(- 2 ， 8)$ B、 $(- 2 ， 2)$ C、 $(- 7 ， - 3)$ D、 $(3 ， - 3)$

查看试题解析
4. 下列调查中，适合采用全面调查方式的是（）

A、了解某班40名学生视力情况 B、对市场上凉糕质量情况的调查 C、对某类烟花爆竹燃放质量情况的调查 D、对鄂旗水质情况的调查

查看试题解析
5.
如图，将三角板的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为（　　）

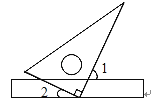A、10° B、15° C、25° D、35°

查看试题解析
6. 在平面直角坐标系中，点P的横坐标是-3，且点P到x轴距离为5，则点P的坐标是（）

A、（5，-3）或（-5，-3） B、（-3，5）或（-3，-5） C、（-3，5） D、（-3，-3）

查看试题解析
7. 为了测算一块600亩试验田里新培育的杂交水稻的产量，随机对其中的10亩杂交水稻的产量进行了检测，在这个问题中，数字10是（）

A、个体 B、总体 C、样本容量 D、总体的样本

查看试题解析
8. 已知甲、乙、丙三个数，甲=5+ $\sqrt{13}$ ，乙=2+ $\sqrt{19}$ ，且甲＞丙＞乙，则下列符合条件的丙是（）

A、1+ $\sqrt{23}$ B、4+ $\sqrt{26}$ C、4+ $\sqrt{15}$ D、4+ $\sqrt{3}$

查看试题解析
9. 线段MN是由线段EF经过平移得到的，若点E(﹣1，3)的对应点M(2，5)，则点F(﹣3，﹣2)的对应点N的坐标是（）

A、(﹣1，0) B、(﹣6，0) C、(0，﹣4) D、(0，0)

查看试题解析
10. 已知 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ 是二元一次方程组 ${\begin{cases} a x + b y = 7 \\ a x - b y = 1 \end{cases}$ 的解，则a-b的值为（）

A、-1 B、1 C、2 D、3

查看试题解析

二、填空题

11. （﹣0.7）² 的平方根是．

查看试题解析
12. 由4x﹣3y+6=0，可以得到用y表示x的式子为x=.

查看试题解析
13. 已知（2x＋3y－4）²＋|x＋3y－7|＝0，则x＝， y＝．

查看试题解析
14. 已知线段 $D E$ 是由线段 $A B$ 平移得到的，且 $A B = D C = 4 c m ， E C = 3 c m$ ，则 $△ D C E$ 的周长为

查看试题解析
15. 如图，将直径为 $2 c m$ 的半圆水平向左平移 $2 c m$ ，则半圆所扫过的面积（阴影部分）为 $c m^{2}$ ．

查看试题解析
16. 已知关于 x 的不等式 x+a≤1 的解集是如图所示，则 a 的值为.

查看试题解析
17. 如果 $B (m + 1 ， 3 m - 5)$ 到x轴的距离与它到y轴的距离相等，则 $m =$

查看试题解析
18. 在平面直角坐标系中，点 $P (x ， y)$ 经过某种变换后得到点 $P^{^{'}} (- y + 1 ， x + 2)$ ，我们把点 $P^{^{'}} (- y + 1 ， x + 2)$ 叫做点 $P (x ， y)$ 的终结点已知点 $P_{1}$ 的终结点为 $P_{2}$ 点 $P_{2}$ 的终结点为 $P_{3}$ ，点 $P_{3}$ 的终结点为 $P_{4}$ ，这样依次得到 $P_{1} ， P_{2} ， P_{3} ， P_{4} ， \dots ， P_{n} ， \dots$ ，若点 $P_{1}$ 的坐标为 $(2 ， 0)$ ，则点 $P_{2021}$ 的坐标为

查看试题解析

三、解答题

19. 解方程组：

(1)、 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = 5 \end{array}$

(2)、 ${\begin{array}{l} 0.2 x + 0.6 y = 1.5 \\ 0.15 x - 0.3 y = 0.5 \end{array}$

查看试题解析
20. 解不等式组 ${\begin{array}{l} 2 x - 1 < 3 \\ 2 x + 5 \leq 3 (x + 2) \end{array}$ ，并把解集在数轴上表示出来

查看试题解析
21. 已知：如图， $∠ C D G = ∠ B$ ， $A D ⊥ B C$ 于点D， $E F ⊥ B C$ 于点F，试判断 $∠ 1$ 与 $∠ 2$ 的关系，并说明理由． $($ 写出推理依据 $)$

查看试题解析
22. 某中学开展“阳光体育一小时”活动，根据学校实际情况，决定开设A：踢毽子；B：篮球；C：跳绳；D：乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题：

(1)、本次共调查了多少名学生？

(2)、请将两个统计图补充完整.

(3)、若该中学有1200名学生，喜欢篮球运动项目的学生约有多少名？

查看试题解析
23. 如图，已知 $A (- 4 ， - 1)$ ， $B (- 5 ， - 4)$ ， $C (- 1 ， - 3)$ ， $Δ A B C$ 经过平移得到的 $Δ A^{'} B^{'} C^{'}$ ， $Δ A B C$ 中任意一点 $P (x_{1} ， y_{1})$ 平移后的对应点为 $P^{'} (x_{1} + 6 ， y_{1} + 4)$ ．

(1)、请在图中作出 $Δ A^{'} B^{'} C^{'}$ ；

(2)、写出点 $A^{'}$ 、 $B^{'}$ 、 $C^{'}$ 的坐标．

查看试题解析
24. 已知，如图，AB∥CD，EG 平分∠BEF，FG 平分∠EFD，求证：∠EGF=90°

查看试题解析
25. 某高校共有5个大餐厅和2个小餐厅．经过测试：同时开放1个大餐厅、2个小餐厅，可供1680名学生就餐；同时开放2个大餐厅、1个小餐厅，可供2280名学生就餐．

(1)、求1个大餐厅、1个小餐厅分别可供多少名学生就餐；

(2)、若7个餐厅同时开放，能否供全校的5300名学生就餐？请说明理由．

查看试题解析