辽宁省沈阳市铁西区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-15 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、a2•a3=a4 B、(a2)3=a5 C、(a+1)2=a2+1 D、(a+2)(a﹣2)=a2﹣42. 下列图案中,是轴对称图形的有( )A、
 B、
B、 C、
C、 D、
D、 3. 下列是随机事件的是( )A、口袋里共有5个球,都是红球,从口袋里摸出1个球是黄球 B、平行于同一条直线的两条直线平行 C、掷一枚图钉,落地后图钉针尖朝上 D、掷一枚质地均匀的骰子,掷出的点数是74. 如图,直线ABCD,且AC⊥CB于点C,若∠BCD=55°,则∠BAC的度数为( )
3. 下列是随机事件的是( )A、口袋里共有5个球,都是红球,从口袋里摸出1个球是黄球 B、平行于同一条直线的两条直线平行 C、掷一枚图钉,落地后图钉针尖朝上 D、掷一枚质地均匀的骰子,掷出的点数是74. 如图,直线ABCD,且AC⊥CB于点C,若∠BCD=55°,则∠BAC的度数为( )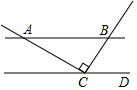 A、65° B、55° C、45° D、35°5. 计算的结果是( )A、 B、 C、 D、6. 如图,已知△ABD和△ABC中,∠DAB=∠CAB,下列条件不能说明△ABD≌△ABC的是( )
A、65° B、55° C、45° D、35°5. 计算的结果是( )A、 B、 C、 D、6. 如图,已知△ABD和△ABC中,∠DAB=∠CAB,下列条件不能说明△ABD≌△ABC的是( )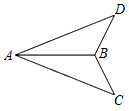 A、BD=BC B、∠D=∠C C、∠ABD=∠ABC D、AD=AC7. 李强同学去登山,先匀速登上山顶,原地休息一段时间后,又匀速下山,上山的速度小于下山的速度.在登山过程中,他行走的路程S随时间t的变化规律的大致图象是( )A、
A、BD=BC B、∠D=∠C C、∠ABD=∠ABC D、AD=AC7. 李强同学去登山,先匀速登上山顶,原地休息一段时间后,又匀速下山,上山的速度小于下山的速度.在登山过程中,他行走的路程S随时间t的变化规律的大致图象是( )A、 B、
B、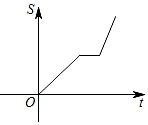 C、
C、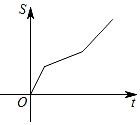 D、
D、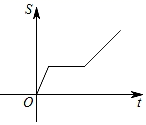 8. 如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,DE⊥AC,垂足为点E,若BD=2,则DE的长为( )
8. 如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,DE⊥AC,垂足为点E,若BD=2,则DE的长为( )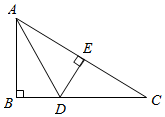 A、3 B、 C、2 D、69. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )
A、3 B、 C、2 D、69. 如果小球在如图所示的地面上自由滚动,并随机停留在某块方砖上,那么它最终停留在黑色区域的概率是( )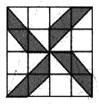 A、 B、 C、 D、10. 下列结论:①a(b+c)=ab+ac;②a(b﹣c)=ab﹣ac;③a5÷a2×a=a3;④(b﹣c)÷a=b÷a﹣c÷a(a≠0).其中一定成立的是( )A、①②③④ B、①②④ C、①③④ D、②③④
A、 B、 C、 D、10. 下列结论:①a(b+c)=ab+ac;②a(b﹣c)=ab﹣ac;③a5÷a2×a=a3;④(b﹣c)÷a=b÷a﹣c÷a(a≠0).其中一定成立的是( )A、①②③④ B、①②④ C、①③④ D、②③④二、填空题
-
11. 数0.0000108用科学记数法表示为 .12. 如图,在△ABC和△ADC中,AB=AD,BC=DC,∠B=128°,则∠D=°.
 13. 为庆祝建党100周年,某校团委给学生布置了一项课外作业,从以下五个内容中任选一个内容制作手抄报:A、“北斗卫星”;B、“5G时代”;C.“智轨快运系统”;D、“东风快递”;E、“高铁”.统计同学们所选内容的人数,绘制成如图所示的折线统计图,则选择E、“高铁”的频率是 .
13. 为庆祝建党100周年,某校团委给学生布置了一项课外作业,从以下五个内容中任选一个内容制作手抄报:A、“北斗卫星”;B、“5G时代”;C.“智轨快运系统”;D、“东风快递”;E、“高铁”.统计同学们所选内容的人数,绘制成如图所示的折线统计图,则选择E、“高铁”的频率是 .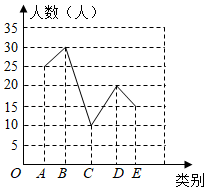 14. 如图,在△ABC中,AB=AC,∠C=62°,点D是BC边上任意一点,过点D作DF//AB交AC于点E,则∠AEF的度数是 .
14. 如图,在△ABC中,AB=AC,∠C=62°,点D是BC边上任意一点,过点D作DF//AB交AC于点E,则∠AEF的度数是 . 15. 如图,线段AB,BC的垂直平分线l1 , l2相交于点O,连接OA,OC,AC,若∠ABC=40°,则∠OAC=°.
15. 如图,线段AB,BC的垂直平分线l1 , l2相交于点O,连接OA,OC,AC,若∠ABC=40°,则∠OAC=°.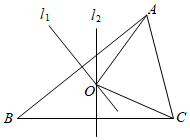 16. 如图(1)是一个长为2a,宽为2b的长方形,用剪刀沿图中虚线剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,中间空余部分的面积是16,若a=b,则原长方形的周长为 .
16. 如图(1)是一个长为2a,宽为2b的长方形,用剪刀沿图中虚线剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,中间空余部分的面积是16,若a=b,则原长方形的周长为 .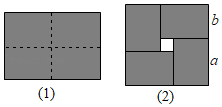
三、解答题
-
17. 先化简,再求值:[(x+1)(x﹣2)+2]÷x,其中x=6.18. 尺规作图题(不写作图步骤,保留作图痕迹).
已知:如图,求作线段AB的垂直平分线.
 19. 如图,在△ABC中,点M,N分别是AB和AC上的点,MN//BC,且BC=4MN,点E是CN的中点,连接ME并延长交BC的延长线于点D.若CD=4,求BC的长.
19. 如图,在△ABC中,点M,N分别是AB和AC上的点,MN//BC,且BC=4MN,点E是CN的中点,连接ME并延长交BC的延长线于点D.若CD=4,求BC的长.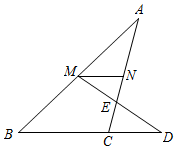 20. 如图,点E,F在分别在直线AB,CD上,∠AEF=70°,EM平分∠AEF交CD于点P,点N在直线CD上,且PN=PM,连接MN,若∠PMN=72.5°,判断直线AB与CD是否平行?并说明理由.
20. 如图,点E,F在分别在直线AB,CD上,∠AEF=70°,EM平分∠AEF交CD于点P,点N在直线CD上,且PN=PM,连接MN,若∠PMN=72.5°,判断直线AB与CD是否平行?并说明理由.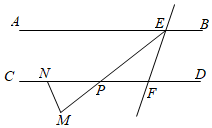 21. 已知长方形的长为8,宽为x,周长为y,面积为S.(1)、y与x之间的关系式为:;(2)、S与x之间的关系式为:;(3)、当S=80时,求y的值.22. 现有甲、乙两个不透明的袋子,甲袋子里装有1个红球,1个黄球;乙袋子里装有1个红球,1个白球,这些球除颜色外其余完全相同.(1)、从甲袋子里随机摸出一个球,则摸到红球的概率为;(2)、从甲袋子里随机摸出一个球,再从乙袋子里随机摸出一个球,求摸出的两个球颜色相同的概率是多少?23. 如图,在△ABC中,∠B=26°,BC的垂直平分线分别交AB,BC于点D,E.若CA=CD,求∠ACB的度数.
21. 已知长方形的长为8,宽为x,周长为y,面积为S.(1)、y与x之间的关系式为:;(2)、S与x之间的关系式为:;(3)、当S=80时,求y的值.22. 现有甲、乙两个不透明的袋子,甲袋子里装有1个红球,1个黄球;乙袋子里装有1个红球,1个白球,这些球除颜色外其余完全相同.(1)、从甲袋子里随机摸出一个球,则摸到红球的概率为;(2)、从甲袋子里随机摸出一个球,再从乙袋子里随机摸出一个球,求摸出的两个球颜色相同的概率是多少?23. 如图,在△ABC中,∠B=26°,BC的垂直平分线分别交AB,BC于点D,E.若CA=CD,求∠ACB的度数. 24. 在△ABC中,点D,E分别在边AC,BC上,点P是边AB上的一个动点,
24. 在△ABC中,点D,E分别在边AC,BC上,点P是边AB上的一个动点,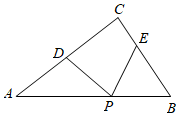 (1)、如图,若∠ACB=90°,
(1)、如图,若∠ACB=90°,①当∠DPE=75°时,求∠ADP+∠BEP的度数;
②当∠DPE=60°时,则∠ADP+∠BEP= ▲ °;
(2)、若∠ACB=m,当∠DPE=n时,请直接用含m,n的式子表示∠ADP+∠BEP的度数.25. 如图,在△ABC中,AB=AC,∠BAC=50°,AD⊥BC于点D,点E为边AD上一点,以AE为腰在直线AD左侧作等腰三角形AEF,使AF=AE,∠EAF=50°,EF与AB交于点G,连接BE,BF.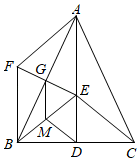 (1)、求∠FAG的度数;(2)、请判断BE与BF是否相等?并说明理由;(3)、点M为BE上一点,连接DM,GM,CE,若GMBF,DMCE,请直接写出∠DMG的度数.
(1)、求∠FAG的度数;(2)、请判断BE与BF是否相等?并说明理由;(3)、点M为BE上一点,连接DM,GM,CE,若GMBF,DMCE,请直接写出∠DMG的度数.