辽宁省沈阳市和平区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-15 类型:期末考试
一、单选题
-
1. 下列运算中,正确的是( )A、2a3•a4=2a7 B、3x2÷2x=x C、(3m2)3=9m6 D、(x﹣1)2=x2﹣12. 在高海拔(1500~3500m为高海拔,3500~5500m为超高海拔,5500m以上为极高海拔)地区的人有缺氧的感觉,下面是有关海拔高度与空气含氧量之间的一组数据:
海拔高度/m
0
1000
2000
3000
4000
5000
6000
7000
空气含氧量/(g/m3)
299.3
265.5
234.8
209.63
182.08
159.71
141.69
123.16
在海拔高度3000m的地方空气含氧量是( )g/m3 .
A、299.3 B、209.63 C、182.08 D、159.713. 下列说法不正确的是( )A、如果明天降水的概率是50%,那么明天有半天都在降雨 B、“从一个只有红球的袋子里面摸出一个球是红球”是必然事件 C、“度量三角形的内角和,结果是360°”是不可能事件 D、随机事件发生的概率介于0和1之间4. 如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是( )A、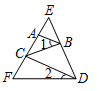 B、
B、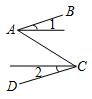 C、
C、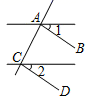 D、
D、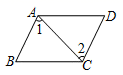 5. 如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
5. 如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( ) A、15 B、10 C、8 D、56. 如图,直线a//b,将一个直角三角尺按如图所示的位置摆放,若∠1=60°,则∠2余角的度数为( )
A、15 B、10 C、8 D、56. 如图,直线a//b,将一个直角三角尺按如图所示的位置摆放,若∠1=60°,则∠2余角的度数为( ) A、30° B、45° C、60° D、150°7. 柿子熟了,从树上落下来,下面的哪一幅图可以大致刻画出柿子下落过程中(即落地前)的速度变化情况( )A、
A、30° B、45° C、60° D、150°7. 柿子熟了,从树上落下来,下面的哪一幅图可以大致刻画出柿子下落过程中(即落地前)的速度变化情况( )A、 B、
B、 C、
C、 D、
D、 8. 空气的密度是1.293×10﹣3g/cm3 , 用小数把它表示出来是( )g/cm3 .A、0.0001293 B、0.001293 C、0.01293 D、0.12939. 若2x=8,4y=16,则2x+2y的值为( )A、 B、﹣2 C、64 D、12810. 如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
8. 空气的密度是1.293×10﹣3g/cm3 , 用小数把它表示出来是( )g/cm3 .A、0.0001293 B、0.001293 C、0.01293 D、0.12939. 若2x=8,4y=16,则2x+2y的值为( )A、 B、﹣2 C、64 D、12810. 如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )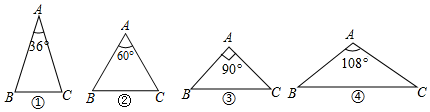 A、①②④ B、②③④ C、①②③ D、①③④
A、①②④ B、②③④ C、①②③ D、①③④二、填空题
-
11. 下列图案是轴对称图形的有 个.
 12. 一个可以自由转动的圆形转盘,转盘分三个扇形区域,分别涂上红、黄、白三种颜色,其中红色、黄色、白色区域的扇形圆心角度数分别为70°,80°,210°,则指针落在红色区域的概率是13. 如图,△ABC中,已知底边BC上的高AD是8,动点Q从点C沿CB向点B运动,设CQ长为x,△ACQ的面积为s,则S与x的关系式为
12. 一个可以自由转动的圆形转盘,转盘分三个扇形区域,分别涂上红、黄、白三种颜色,其中红色、黄色、白色区域的扇形圆心角度数分别为70°,80°,210°,则指针落在红色区域的概率是13. 如图,△ABC中,已知底边BC上的高AD是8,动点Q从点C沿CB向点B运动,设CQ长为x,△ACQ的面积为s,则S与x的关系式为 14. 已知∠A和∠B的两边分别平行,若∠A=70°,则∠B的度数为 .15. 计算:3(22+1)(24+1)…(232+1)﹣1,它的结果的个位数字是 .16. 如图,CA⊥AB,垂足为点A,AB=8cm,AC=4cm,射线BM⊥AB,垂足为点B,一动点E从A点出发,以2cm/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动秒时,点B、D、E组成的三角形与点A、B、C组成的三角形全等.
14. 已知∠A和∠B的两边分别平行,若∠A=70°,则∠B的度数为 .15. 计算:3(22+1)(24+1)…(232+1)﹣1,它的结果的个位数字是 .16. 如图,CA⊥AB,垂足为点A,AB=8cm,AC=4cm,射线BM⊥AB,垂足为点B,一动点E从A点出发,以2cm/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动秒时,点B、D、E组成的三角形与点A、B、C组成的三角形全等.
三、解答题
-
17. 计算: .18. 先化简,再求值:[(10+x)(600﹣10x)﹣6000]÷5x.其中x=﹣1.19. 如图,∠1=∠2,∠3=∠C,∠4=∠5.请说明BF//DE的理由.(请在括号中填上推理依据)

解:∵∠1=∠2(已知)
∴CF//BD( ▲ )
∴∠3+∠CAB=180°( ▲ )
∵∠3=∠C(已知)
∴∠C+∠CAB=180°(等式的性质)
∴AB//CD( ▲ )
∴∠4=∠EGA(两直线平行,同位角相等)
∵∠4=∠5(已知)
∴∠5=∠EGA(等量代换)
∴ED//FB( ▲ )
20. 如图所示有8张卡片,分别写有1,2,3,4,5,6,8,9这八个数字,将它们背面朝上洗匀后,任意抽出一张. (1)、P(抽到数字9)=;(2)、P(抽到两位数)=;(3)、P(抽到的数大于5)=;(4)、P(抽到偶数)= .21. 尺规作图:(不写作法,保留作图痕迹)已知:线段a,c,∠α.求作:△ABC,使BC=a,AB=c,∠BAC=∠a.
(1)、P(抽到数字9)=;(2)、P(抽到两位数)=;(3)、P(抽到的数大于5)=;(4)、P(抽到偶数)= .21. 尺规作图:(不写作法,保留作图痕迹)已知:线段a,c,∠α.求作:△ABC,使BC=a,AB=c,∠BAC=∠a. 22. 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在点上)
22. 如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在点上) (1)、在图中作出△ABC关于直线对称的△A1B1C1(点A的对应点是点A1 , 点B的对应点是点B1 , 点C的对应点是点C1);(2)、在直线l上画出点P,使PA+PC最小;(3)、直接写出△A1BC的面积为 .23. 如图,△ABC是等边三角形,点D是△ABC内一点,连接AD,BD,CD,∠BDC=100°,以AD为一边在AD左侧作等边三角形ADE,连接CE.
(1)、在图中作出△ABC关于直线对称的△A1B1C1(点A的对应点是点A1 , 点B的对应点是点B1 , 点C的对应点是点C1);(2)、在直线l上画出点P,使PA+PC最小;(3)、直接写出△A1BC的面积为 .23. 如图,△ABC是等边三角形,点D是△ABC内一点,连接AD,BD,CD,∠BDC=100°,以AD为一边在AD左侧作等边三角形ADE,连接CE. (1)、△ABD与△ACE全等吗?说明你的理由;
(1)、△ABD与△ACE全等吗?说明你的理由;解:△ABD≌△ACE,理由如下:
∵△ABC与△ADE都是等边三角形
∴AB=AC
AD=AE
∠CAB=∠EAD=60°
∴∠CAB﹣∠CAD=∠EAD﹣∠CAD
∴∠DAB=∠EAC
在△ABD与△ACE中
, ,
∴ .
(2)、当∠ADB=150°时,请判断△CDE的形状,并说明理由;(3)、当△CDE是等腰三角形时,请直接写出∠ADB的度数为 .24. 某数学活动小组结合图象设计如下情景:已知家、书店、学校依次在同一条直线上,书店离家8km,学校离家25km,小明从家出发,匀速骑行0.4h到达书店;在书店停留0.6h后,匀速骑行1h到达学校;在学校学习一段时间,然后回家;回家途中,匀速骑行1h后减速,继续匀速骑行回到家.给出的图象反映了这个过程中小明离家的距离与离开家的时间之间的对应关系.
请根据相关信息解答下列问题:
(1)、填表:离开家的时间/h
0.3
0.8
1.6
3
4.5
5.2
离开家的距离/km
(2)、填空:①书店到学校的距离为km;
②从学校回家途中减速前的骑行速度为;
③当小明离家的距离为2km时,他离开家的时间为 .
25. 如图,在△ABC中,AC=BC,点D在边AB上,AB=4BD,连接CD,点E,F在线段CD上,连接BF,AE,∠BFC=∠AEC=180°-∠ACB. (1)、①∠FBC与∠ECA相等吗?说明你的理由;
(1)、①∠FBC与∠ECA相等吗?说明你的理由;②△FBC与△ECA全等吗?说明你的理由;
(2)、若AE=11,EF=8,则请直接写出BF的长为;(3)、若△ACE与△BDF的面积之和为12,则△ABC的面积为 .