辽宁省葫芦岛市绥中县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列有理数中，比0小的数是（）

A、﹣3 B、1 C、2 D、3

查看试题解析
2. 若a＜b，则下列不等式中正确的是（）

A、a﹣3＞b﹣3 B、a﹣b＜0 C、 $\frac{1}{3}$ a $＞ \frac{1}{3}$ b D、﹣4a＜﹣4b

查看试题解析
3. 在平面直角坐标系中，将点A（x，y）向左平移5个单位长度，再向下平移3个单位长度后与点B（﹣1，2）重合，则点A的坐标是（）

A、（4，5） B、（﹣6，﹣1） C、（﹣4，5） D、（﹣4，﹣1）

查看试题解析
4. 下列调查中，适合采用全面调查方式的是（）

A、调查某批次汽车的抗撞击能力 B、了解全国快递包裹产生垃圾的数量 C、了解某班学生的身高情况 D、鞋厂检测生产的鞋底能承受的弯折程度

查看试题解析
5. 为了丰富学生的课外小组活动，学生手工社团准备长5m的彩绳，截成1m或2m两种规格的彩绳，用来做手工编织，在不造成浪费的前提下，有（）不同的截法．

A、2种 B、3种 C、4种 D、5种

查看试题解析
6. 如图，直线 $A B // C D$ ，且 $A C ⊥ C B$ 于点 $C$ ，若 $∠ B A C = 35 °$ ，则 $∠ B C D$ 的度数为（）

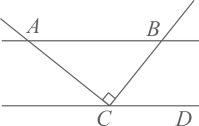A、65° B、55° C、45° D、35°

查看试题解析
7. 如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为（）

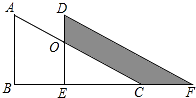A、48 B、96 C、84 D、42

查看试题解析
8. 已知关于x，y的二元一次方程组 ${\begin{array}{l} a x + b y = 8 \\ b x - a y = 1 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则2a﹣b的值是（）

A、﹣1 B、1 C、3 D、4

查看试题解析
9. 不等式组 ${\begin{array}{l} 3 + x > 1 \\ 2 x - 3 \leq 1 \end{array}$ 的整数解的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
10. 如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长度，P₁ ， P₂ ， P₃ ， …均在格点上，其顺序按图中“→”方向排列，如：P₁（0，0），P₂（0，1），P₃（1，1），P₄（1，﹣1），P₅（﹣1，﹣1），P₆（﹣1，2）…根据这个规律，点P₂₀₂₁的坐标为（）

A、（﹣505，﹣505） B、（﹣505，506） C、（506，506） D、（505，﹣505）

查看试题解析

二、填空题

11. 比较大小： $- \sqrt{65}$ ﹣8．

查看试题解析
12. 为了考察某区3500名毕业生的数学成绩，从中抽出20本试卷，每本30份，在这个问题中，样本容量是．

查看试题解析
13. 不等式2x+5＜10的正整数解是．

查看试题解析
14. 已知 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是二元一次方程ax﹣2＝﹣by的一个解，则2a﹣b﹣6的值等于．

查看试题解析
15. 已知平面直角坐标系中，点M（a，1﹣3a）在第四象限，那么a的取值范围是．

查看试题解析
16. 已知如图，直线AB、CD相交于O，∠AOC＝60°，OE平分∠DOB，则∠COE的度数是．

查看试题解析
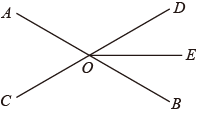17. 已知点A（m﹣1，﹣5）和点B（2，m+1），若直线AB∥x轴，则线段AB的长是．

查看试题解析
18. 已知三条不同的直线a、b、c在同一平面内，下列四条命题：
①如果a∥b，a⊥c，那么b⊥c； ②如果b∥a，c∥a，那么b∥c；
③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c．
其中真命题的是．（填写所有真命题的序号）

查看试题解析
19. 某市在落实国家“精准扶贫”政策的过程中，为某村修建一条长为400米的公路，由甲、乙两个工程队负责施工．甲工程队独立施工两天后，乙工程队加入，两工程队联合施工3天后，还剩50米的工程．已知甲工程队每天比乙工程队多施工2米，求甲、乙工程队每天各施工多少米．设甲工程队每天施工x米，乙工程队每天施工y米，根据题意，列出方程组．

查看试题解析
20. 关于x的不等式组 ${\begin{array}{l} 2 x < 3 (x - 3) + 1 \\ \frac{3 x + 2}{4} > x + a \end{array}$ 有四个整数解，则a的取值范围是.

查看试题解析

三、解答题

21. 计算： $\sqrt{16} - \sqrt[3]{- 8} - \sqrt[3]{1} -$ | $\sqrt{2} -$ 2|．

查看试题解析
22. 已知3既是a﹣1的算术平方根，又是a+2b+1的立方根，求a²﹣b²的平方根．

查看试题解析
23. 已知关于x，y的二元一次方程组 ${\begin{array}{l} x + 2 y = 3 ， \\ 3 x + 5 y = m + 2 \end{array}$ 的解满足 $x + y = 0$ ，求实数m的值.

查看试题解析
24. 解不等式 $\frac{4 + 3 x}{6} \leq \frac{1 + 2 x}{3} + 1$ ，并在数轴上表示解集，并写出它的非正整数解．

查看试题解析
25. 如图，一只蚂蚁从点A沿数轴向右直爬2个单位到达点B，点A表示 $- \sqrt{2}$ ，设点B所表示的数为m．

(1)、求m的值；

(2)、求|m﹣1|+（m﹣6）的值．

查看试题解析
26. 如图，已知AB∥CD，∠B＝70°，CM平分∠BCE，∠MCN＝90°，求∠DCN的度数．

查看试题解析
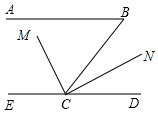27. 在平面直角坐标系中，已知点A（﹣4，3）、B（﹣2，﹣2）．

(1)、描出A、B两点的位置，并连接AB、AO、BO．

(2)、△AOB的面积是．

(3)、把△AOB向右平移4个单位，再向上平移3个单位，画出平移后的△A₁O₁B₁ ，并写出各点的坐标．

查看试题解析
28. 如图，点O在直线AB上，OC⊥OD，∠EDO与∠1互余．

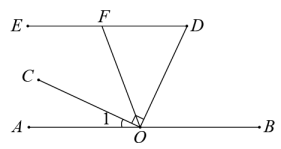(1)、求证：ED∥AB；

(2)、OF平分∠COD交DE于点F，若∠OFD＝65°，求∠1的度数．

查看试题解析
29. 某市为了将生活垃圾合理分类，并更好地回收利用，将垃圾分为可回收物、厨余垃圾、有害垃圾和其他垃圾四类.现随机抽取该市 $m$ 吨垃圾，将调查结果制成如下两幅不完整的统计图：

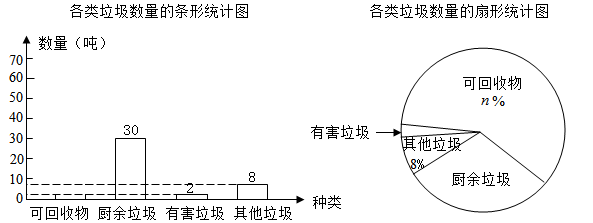
根据统计图提供的信息，解答下列问题：

(1)、 $m =$ ， $n =$ ；

(2)、根据以上信息直接在答题卡中补全条形统计图；

(3)、扇形统计图中，厨余垃圾所对应的扇形圆心角的度数为度；

(4)、根据抽样调查的结果，请你估计该市200吨垃圾中约有多少吨可回收物.

查看试题解析