辽宁省葫芦岛市建昌县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，最大的是（）

A、3.14 B、0 C、 $π$ D、 $- \sqrt{3}$

查看试题解析
2. 在平面直角坐标系中，点P（－2，2）位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 如图所示的各组图形中，表示平移关系的是（）

A、 B、 C、 D、

查看试题解析
4. 若x＞y，则下列式子不正确的是（）

A、x﹣3＞y﹣3 B、﹣3x＞﹣3y C、x+3＞y+3 D、 $\frac{x}{3} > \frac{y}{3}$

查看试题解析
5. 如图，直线AB与直线CD相交于点O，MO⊥AB，垂足为O.已知∠AOD＝136°，则∠COM的度数为（）

A、36° B、44° C、46° D、54°

查看试题解析
6. 不等式组 ${\begin{array}{l} \frac{1}{2} (x + 1) \leq 2 \\ x - 3 < 3 x + 1 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，学校 $A$ 在蕾蕾家 $B$ 南偏西 $25 °$ 的方向上，点 $C$ 表示超市所在的位置， $∠ A B C = 90 °$ ，则超市 $C$ 在蕾蕾家的（）

A、北偏东 $55 °$ 的方向上 B、南偏东 $55 °$ 的方向上 C、北偏东 $65 °$ 的方向上 D、南偏东 $65 °$ 的方向上

查看试题解析
8. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于 $x ， y$ 的二元一次方程 $x + a y = - 1$ 的一个解，则a的值为（）

A、1 B、0 C、 $- \frac{1}{2}$ D、 $- 1$

查看试题解析
9. 如图所示，P是直线l外一点，点A，B，C在l上，且PB⊥l，垂足是B，下列说法：①PA，PB，PC这3条线段中，PB最短；②点P到直线l的距离是线段PB的长；③线段AB的长是点A到PB的距离；④线段PA的长是点P到直线l的距离．其中正确的是（）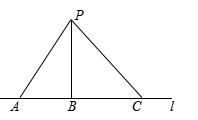

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
10. 如图，将一块长方形纸条折成如图的形状，若已知 $∠ 1 = α$ ，则 $∠ 2$ 的度数为（）

A、 $90 ° - α$ B、 $90 ° + α$ C、 $90 ° - \frac{α}{2}$ D、 $90 ° + \frac{α}{2}$

查看试题解析

二、填空题

11. $\sqrt{16}$ 的算术平方根是

查看试题解析
12. $\sqrt[3]{- 8} \times \sqrt{9} - \sqrt{\frac{25}{4}} =$ ．

查看试题解析
13. 比较大小：3 $\sqrt{10}$ （填＜，＞或＝）．

查看试题解析
14. 把命题“同角的余角相等”改写成“如果…那么…”的形式．

查看试题解析
15. 将方程 $2 x + y = 1$ 变形为用含x的式子表示y的形式，则 $y =$ ．

查看试题解析
16. “了解我省七年级学生的视力情况”适合做调查（填“全面”或“抽样”）．

查看试题解析
17. 已知点 $A (3 ， 0)$ ，点 $B$ 在 $y$ 轴上， $S_{△ A B O} = 6$ ，则 $B$ 点坐标为．

查看试题解析
18. 一副三角板按如图所示叠放在一起，其中点B、D重合，若固定三角形AOB，改变三角板ACD的位置（其中A点位置始终不变），下列条件①∠BAD＝30°；②∠BAD＝60°；③∠BAD＝120°；④∠BAD＝150°中，能得到的CD∥AB的有．（填序号）

查看试题解析

三、解答题

19. 解方程组 ${\begin{array}{l} y = 5 - 2 x \\ 3 x + 2 y = 4 \end{array}$

查看试题解析
20. 解不等式： $\frac{1 + x}{2} - \frac{2 x - 1}{3} \leq 1$ ，并把解集在数轴上表示出来.

查看试题解析
21. 在如图所示的方格图中，我们称每个小正方形的顶点为“格点”，以格点为顶点的三
角形叫做“格点三角形”，根据图形，回答下列问题.

(1)、图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的？

(2)、如果以直线a，b为坐标轴建立平面直角坐标系后，点A的坐标为(－3，4)，请写出格点三角形DEF各顶点的坐标，并求出三角形DEF的面积.

查看试题解析
22. 几何说理填空：如图，F是BC上一点，FG⊥AC于点G，H是AB上一点，HE⊥AC于点E，∠1＝∠2，求证：DE∥BC．
证明：连接EF
∵FG⊥AC，HE⊥AC，
∴∠FGC＝∠HEC＝90°（   ▲   ）．
∴   ▲   ∥   ▲   （   ▲   ）．
∴∠3＝∠   ▲   （   ▲   ）．
又∵∠1＝∠2，
∴∠1+∠3＝∠2+∠4．
即∠DEF＝∠EFC
∴DE∥BC（   ▲   ）．

查看试题解析
23. 为了加强学生安全教育，某市某中学举行了一次“安全知识竞赛”，共有1600名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）进行统计．请你根据下面的频数分布表和频数分布直方图，解答下列问题：
分组
频数
百分比
50.5≤x＜60.5
4
10%
60.5≤x＜70.5
a
20%
70.5≤x＜80.5
12
30%
80.5≤x＜90.5
10
25%
90.5≤x＜100.5
b
15%
合计
40
100%

(1)、频数分布表中 $a =$ ， $b =$ ；

(2)、抽取的样本容量是，请补全频数分布直方图．

(3)、若成绩在80分以上（不含80分）为优秀，估计该校成绩达到优秀的学生有多少人．

查看试题解析
24. 列二元一次方程组或一元一次不等式解决实际问题：
某汽车专卖店销售A，B两种型号的新能源汽车，已知1辆A型车和2辆B型车共销售70万元，3辆A型车和1辆B型车共销售80万元．

(1)、每辆A型车和B型车的售价各为多少万元？

(2)、甲公司拟向该店购买A，B两种型号的新能源汽车共7辆，购车费不少于154万元，求最多可购进A型车多少辆？

查看试题解析
25. 如图，AE平分∠BAC，∠CAE＝∠CEA．（此题解题过程不写根据）

(1)、如图1，求证：AB∥CD；

(2)、如图2，点F为线段AC上一点，连接EF，求证：∠BAF＋∠AFE＋∠DEF＝360°；

(3)、如图2，EF⊥AC于点F，∠DEF＝140°，直接写出∠BAE的度数．

查看试题解析
26. 如图，B（3，5）是平面直角坐标系内一点，BA⊥x轴于点A，BC⊥y轴于点C．

(1)、如图1，直接写出A，C两点的坐标；

(2)、如图2，若过点C的直线CD交AB于点D，且把长方形OABC的周长分为3：1两部分，求点D坐标；

(3)、如图3，将（2）中的线段CD向下平移2个单位，得到C₁D₁ ，直接写出四边形OAD₁C₁的面积．

查看试题解析

分组	频数	百分比
50.5≤x＜60.5	4	10%
60.5≤x＜70.5	a	20%
70.5≤x＜80.5	12	30%
80.5≤x＜90.5	10	25%
90.5≤x＜100.5	b	15%
合计	40	100%