辽宁省大连市高新区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{9}$ 的值等于 $($ $)$

A、3 B、-3 C、±3 D、 $\sqrt{3}$

查看试题解析
2. 在平面直角坐标系中，点 $A (2, - 3)$ 位于哪个象限？（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 若m $>$ n ，则下列各式一定成立的是（　　）

A、m+3 $<$ n+3 B、m﹣3 $<$ n﹣3 C、 $\frac{m}{3} > \frac{n}{3}$ D、﹣3m $>$ ﹣3n

查看试题解析
4. 如右图，下列条件中不能判定AB∥CD的是（）

A、∠1＝∠2 B、∠3＝∠4 C、∠1＋∠4＝180° D、∠1＝∠5

查看试题解析
5. 已知 ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ 是二元一次方程ax+2y＝5的一个解，则a的值为（）

A、 $- \frac{3}{2}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
6. 在实数 $- 3$ ， $- π$ ， $- \sqrt{17}$ ， $- 4$ 中，最小的是（）

A、 $- π$ B、 $- \sqrt{17}$ C、 $- 3$ D、 $- 4$

查看试题解析
7. 从某工厂即将出售的一批产品中抽检 $100$ 件产品，其不合格的产品有 $8$ 件，则此抽样调查的样本中，样本容量和不合格的频率分别是（）

A、 $8$ ， $0.08$ B、 $8$ ， $0.92$ C、 $100$ ， $0.08$ D、 $100$ ， $0.92$

查看试题解析
8. 如图，直线 $A B$ 与 $C D$ 相交于点 $E$ ， $∠ C E B = 45 °$ ， $E F ⊥ A E$ ，则 $∠ D E F$ 的度数为（）

A、 $125 °$ B、 $135 °$ C、 $145 °$ D、 $155 °$

查看试题解析
9. 某车间需加工某种零件500个，若用2台自动化车床和6台普通车床加工一天，则还剩10个零件没加工；若用3台自动化车床和5台普通车床加工一天，则可以超额完成15个零件．如果一台自动化车床和一台普通车床一天加工的零件数分别为x个和y个，则下列所列方程组正确的是（）

A、 ${\begin{array}{l} 2 x + 6 y = 500 + 10 \\ 3 x + 5 y = 500 + 15 \end{array}$ B、 ${\begin{array}{l} 2 x + 6 y = 500 - 10 \\ 3 x + 5 y = 500 - 15 \end{array}$ C、 ${\begin{array}{l} 2 x + 6 y = 500 - 10 \\ 3 x + 5 y = 500 + 15 \end{array}$ D、 ${\begin{array}{l} 2 x + 6 y = 500 + 10 \\ 3 x + 5 y = 500 - 15 \end{array}$

查看试题解析
10. 下列说法：
①实数与数轴上的点一一对应；
②经过直线外一点，有且只有一条直线与这条直线平行；
③若 $a x > a$ ，则 $x > 1$ ．
其中正确的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析

二、填空题

11. 若 $x^{3} = - 64$ ，则 $x =$ ．

查看试题解析
12. “x的3倍与2的差是非负数”用不等式表示为．

查看试题解析
13. 一个不透明的盒子中有若干个白球和 $5$ 个黑球，从中摸出一球记下颜色后放回，重复摸球 $100$ 次，其中摸到黑球的次数为 $25$ 次，盒中有白球约个．

查看试题解析
14. 《九章算术》第八卷方程第十问题：“今有甲、乙二人持钱不知其数，甲得乙半而钱五十，乙得甲太半而亦钱五十.甲、乙持钱各几何？”
题目大意是：甲、乙两人各带了若干钱，如果甲得到乙所有的一半，那么甲共有钱50文，如果乙得到甲所有钱的三分之二，那么乙也共有钱50文.甲、乙各带了多少钱？
设甲原有 $x$ 文钱，乙原有 $y$ 文钱，可列方程组为：.

查看试题解析
15. $A$ 、 $B$ 两点的坐标分别是 $(- 2 ， 1)$ ， $(- 3 ， 3)$ ，若将线段 $A B$ 平移至 $A^{'} B^{'}$ ， $A$ 、 $B$ 的对应点分别为 $A^{'}$ 、 $B^{'}$ ，点 $A^{'}$ 、 $B^{'}$ 的坐标分别为 $(a ， 3)$ ， $(1 ， b)$ ，则 $a + b =$ ．

查看试题解析
16. 如图，将长方形 $A B C D$ 沿 $E F$ 折叠，点 $D$ 落在 $A B$ 边上的 $H$ 点处，点 $C$ 落在点 $G$ 处，若 $∠ A E H = m °$ ，则 $∠ B F G$ 等于 $°$ （用含 $m$ 的式子表示）．

查看试题解析

三、解答题

17. 解不等式组 ${\begin{array}{l} 3 (x - 1) + 2 \leq 5 x + 3 \\ \frac{x}{3} < 1 - \frac{x - 1}{5} \end{array}$ ，并把它的解集在数轴上表示出来，写出不等式组的最大整数解．

查看试题解析
18. 为了解学生网上课堂的学习效果，某中学随机抽取了部分七年级学生进行调查．要求每位学生从“优秀”，“良好”，“一般”，“不合格”四个等次中，选择一项作为自我评价网课学习的效果，现将调查结果绘制成如图两幅不完整的统计图，请结合图中所给的信息解答下列问题．

(1)、这次活动共抽查了人，扇形统计图中，学习效果“一般”的学生人数所在扇形的圆心角度数为 $°$ ；

(2)、若该校七年级学生共有 $600$ 名，根据以上抽样结果，估计该校七年级学生网课学习效果为良好和优秀学生共多少名？

查看试题解析
19. 如图，直线 $A B$ 、 $C D$ 相交于点 $O$ ， $O F ⊥ C D$ ，垂足为 $O$ ，且 $O F$ 平分 $∠ A O E$ ．若 $∠ B O D = 20 °$ ，求 $∠ E O F$ 的度数．

查看试题解析
20. 疫情防控期间，某校开学时购买了 $30$ 瓶 $A$ 类消毒液和 $20$ 瓶 $B$ 类消毒液共花费 $1050$ 元，已知购买 $3$ 瓶 $A$ 类消毒液比购买 $1$ 瓶 $B$ 类消毒液多花 $15$ 元．

(1)、求 $A$ 类消毒液和 $B$ 类消毒液的单价分别为多少钱？

(2)、疫情逐渐得到控制，学校计划用不超过 $500$ 元的经费再次购买 $A$ 类消毒液和 $B$ 类消毒液共 $20$ 瓶，若单价不变，则最多能购买多少瓶 $B$ 类消毒液？

查看试题解析
21. 如图用两个边长为 $\sqrt{18}$ cm的小正方形纸片拼成一个大的正方形纸片，沿着大正方形纸片的边的方向截出一个长方形纸片，能否使截得的长方形纸片长宽之比为 $3 ： 2$ ，且面积为 $30$ cm²？请说明理由．

查看试题解析
22. 如图， $∠ E F C = ∠ A B C$ ， $∠ B E F + ∠ A = 180 °$ ．

(1)、求证 $A D / / B E$ ；

(2)、若 $B E$ 平分 $∠ A B C$ ， $A D ⊥ C D$ 于点 $D$ ， $∠ E F C = 50 °$ ，求 $∠ F E C$ 的度数．

查看试题解析
23. 对 $x$ ， $y$ 定义一种新的运算 $P$ ，规定： $P (x ， y) = {\begin{array}{l} m x + n y ， (x \geq y) \\ n x + m y ， (x < y) \end{array}$ （其中 $m n \neq 0$ ）．已知 $P (2 ， 1) = 7$ ， $P (- 1 ， 1) = - 1$ ．

(1)、求 $m$ 、 $n$ 的值；

(2)、若 $a > 0$ ，解不等式组 ${\begin{array}{l} P (2 a ， a - 1) < 4 \\ P (- \frac{1}{2} a - 1 ， - \frac{1}{3} a) \leq - 5 \end{array}$ ．

查看试题解析
24. 如图，平面直角坐标系中，正方形ABCD的边AB∥y轴，点A（-2，4），点C（4，-2）．

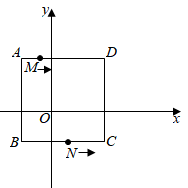(1)、点 $B$ 的坐标为，点 $D$ 的坐标为；

(2)、点M从点A出发，以每秒2个单位长度的速度按顺时针方向，沿正方形的边AD→DC运动到点C停止；点N从点B出发，以每秒3个单位长度的速度按逆时针方向，沿正方形的边BC→CD运动到点D停止．点M与点N同时出发，设点M的运动时间为t（秒），三角形AMN的面积为S（单位²）．
①求点M与点N相遇处的坐标；
②用含t的代数式表示S，并直接写出t的取值范围．

查看试题解析
25. 已知：AB∥CD，直线EF分别交AB、CD于点E、F，直线GH分别交AB、CD于点G，H．

(1)、如图1，若∠BGH=80°，∠BEF=120°，ME平分∠AEF，MH平分∠GHC，求∠EMH的度数；

(2)、如图2，MH平分∠GHC，EN平分∠BEF交MH的延长线于N，探究∠MNE、∠BGH、∠BEF之间的数量关系，并证明；

(3)、如图3，直线EF、GH交于点P，PQ平分∠FPH，FK平分∠PFC，过P作PO∥FK，探究∠QPO与∠PHC之间的数量关系，并证明．

查看试题解析
26. 在平面直角坐标系中，点A（1，2），点B（a，b），且 $\sqrt{- (a - 3)^{2}} = \sqrt{4 - b} + \sqrt{b - 4}$ ，点E（6，0），将线段AB向下平移m个单位（m＞0）得到线段CD，其中A、B的对应点分别为C、D．

(1)、求点 $B$ 的坐标及三角形ABE的面积；

(2)、当线段CD与 $x$ 轴有公共点时，求 $m$ 的取值范围；

(3)、设三角形CDE的面积为 $S$ ，当 $4 \leq S \leq 5$ 时，求 $m$ 的取值范围．

查看试题解析