辽宁省大连市甘井子区2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-15 类型：期末考试

进入出卷网下载

一、单选题

1. 以下调查中，适合全面调查的是（）

A、调查天和核心舱的设备零件的质量情况 B、调查某池塘中现有鱼的数量 C、调查市场上某种食品的色素含量是否符合国家标准 D、调查春节联欢晚会的收视率

查看试题解析
2. 不等式2x+3≥7的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、3.6，3.6，7.2 B、4，4，10 C、5，6，10 D、 $\frac{11}{3}$ ， $\frac{6}{3}$ ， $\frac{5}{3}$

查看试题解析
4. 在平面直角坐标系中，点A（1，1）经过平移后的对应点为B（3，4），下列平移正确的是（）

A、先向右平移2个单位长度，再向下平移3个单位长度 B、先向右平移2个单位长度，再向上平移3个单位长度 C、先向左平移2个单位长度，再向下平移3个单位长度 D、先向左平移2个单位长度，再向上平移3个单位长度

查看试题解析
5. 下列大小关系正确的是（）

A、 $\sqrt{2} -$ 2＞0 B、2 $\sqrt{3} -$ 3＜0 C、 $\frac{\sqrt{5} - 1}{2} ＞$ 1 D、8 $＜ \sqrt{65}$

查看试题解析
6. 为了解某班50名同学对电视节目的喜爱情况进行全面调查，并将调查到的数据绘制成如图所示的扇形统计图，其中A：新闻，B：体育，C：动画，D：娱乐，E：戏曲，则下列说法不正确的是（）

A、喜爱新闻节目的有4人 B、喜爱体育节目的占全班同学的10% C、喜爱娱乐节目的有18人 D、喜爱戏曲节目的占全班同学的6%

查看试题解析
7. 如图，两条直线a，b相交，若2∠3＝3∠1，则以下各角度数正确的是（）

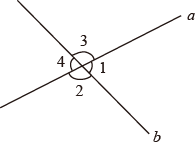A、∠1＝72° B、∠2＝120° C、∠3＝144° D、∠4＝36°

查看试题解析
8. 养牛场原有30头大牛和15头小牛，1天约用饲料675kg；一周后又购进20头大牛和35头小牛，这时1天约用饲料1250kg．求每头大牛和小牛1天各约用饲料多少千克？设每头大牛和小牛1天各约用饲料xkg和ykg，则可列二元一次方程组为（）

A、 ${\begin{array}{l} 30 x + 15 y = 675 \\ 20 x + 35 y = 1250 \end{array}$ B、 ${\begin{array}{l} 30 x + 15 y = 675 \\ 50 x + 50 y = 1925 \end{array}$ C、 ${\begin{array}{l} 30 x + 15 y = 675 \\ 50 x + 50 y = 1250 \end{array}$ D、 ${\begin{array}{l} 20 x + 35 y = 1250 \\ 50 x + 50 y = 1925 \end{array}$

查看试题解析
9. 如图，五边形ABCDE的内角都相等，且∠ADE＝∠DAE，∠BDC＝∠DBC，则∠ADB＝（）

A、18° B、36° C、72° D、108°

查看试题解析
10. 去年某市空气质量良好（二级以上）的天数与全年天数（365）之比达到60%，如果明年（365天）这样的比值要超过70%，那么明年空气质量良好的天数要比去年至少增加多少？设明年比去年空气质量良好的天数增加了x天，则可列一元一次不等式为（）

A、x+365×60%＞365×70% B、x+365×60%≥365×70% C、 $\frac{x + 365 \times 60 %}{365} ＞$ 365×70% D、 $\frac{x + 365 \times 60 %}{365} \geq$ 365×70%

查看试题解析

二、填空题

11. 化简 $| \sqrt{2} - \sqrt{3} |$ = ．

查看试题解析
12. 为了解某校1500名学生的睡眠情况，随机抽取了150名学生作为样本进行调查，则抽取的样本容量是．

查看试题解析
13. 将一块直角三角尺ABC按如图所示的方式放置，其中点A、C分别落在直线a、b上，若a∥b，∠1＝62°，则∠2的度数为．

查看试题解析
14. 我国古代数学著作《九章算术》中记载：“今有大器五小器一容三斛，大器一小器五容二斛.问大小器各容几何.”其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，音hu ，是古代的一种容量单位）.1个大桶加上5个小桶可以盛酒2斛，问1个大桶、一个小桶分别可以盛酒多少斛？若设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据题意，可列方程组为.

查看试题解析
15. 若a＞b，则﹣3.5a+1 ﹣3.5b+1（填“＜”或“＞”）．

查看试题解析
16. 如图，在平面直角坐标系中，正方形OABC的四个顶点坐标分别是O（0，0），A（a² ， 0），B（n，n），C（0，b²），且|n|＝3，ab＞0，则a+b＝．

查看试题解析

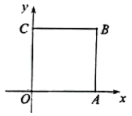
三、解答题

17. 根据表回答问题：
x
16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
16.9
17
$x^{2}$
256
259.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
285.61
289

(1)、 $\sqrt{256} =$ ； $\sqrt{265.7} \approx$ ．

(2)、272.25的平方根是；

(3)、若a，b是表中两个相邻的数，a $＜ \sqrt{280} ＜$ b，则a＝，b＝．

查看试题解析
18. 解下列方程组：

(1)、 ${\begin{array}{l} y = 2 x - 3 \\ 3 x + y = 1 \end{array}$ ；

(2)、 ${\begin{array}{l} 5 a + 2 b = 25 \\ 3 a + 4 b = 15 \end{array}$ ．

查看试题解析
19. 解下列不等式（组）：

(1)、 $\frac{x + 1}{6} \geq \frac{2 x - 5}{4} + 1$ ；

(2)、 ${\begin{array}{l} 5 - (2 x - 1) ＜ - 6 x \\ \frac{1 + 2 x}{3} ＞ x - 1 \end{array}$ ．

查看试题解析
20. 某校为了增强学生垃圾分类的意识，举办了一次全校学生参与的有关垃圾分类的问卷测试（满分100分，得分均为整数），从中随机抽取部分学生的成绩，如图所示绘制了样本的频数分布表和频数分布直方图．
成绩x（分）
频数（人）
百分比
50≤x＜60
12
12%
60≤x＜70
20
a
70≤x＜80
b
c
80≤x＜90
28
28%
90≤x＜100
16
16%
请根据以上图表，回答下列问题：

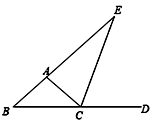
(1)、请直接写出a＝， b＝， c＝．

(2)、补全频数分布直方图；

(3)、若该校有学生1800人，成绩在80分以上为优秀，请你估计该校本次测试成绩优秀的学生有多少人？

查看试题解析
21. 如图，在△ABC中，CD是∠ACB的平分线，E、F分别在边AC，BC上，∠ADE＝∠B，∠DFC+∠ACB＝180°．求证：CD平分∠EDF．

查看试题解析
22. 某农场用2台大收割机和5台小收割机同时工作2小时共收割小麦3.6公顷，3台大收割机和2台小收割机同时工作5小时共收割小麦8公顷.1台大收割机和1台小收割机每小时各收割小麦多少公顷？

查看试题解析
23. 如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，
证明：∠BAC=∠B+2∠E

查看试题解析
24. 如图1，直线AD、BC相交于点O，∠DCP $= \frac{1}{2}$ ∠BCP＝α，∠B＝3α．

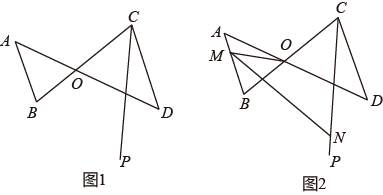(1)、求证：AB∥CD；

(2)、若∠D＝2∠DCP，求∠AOC的度数（用含α的式子表示）；

(3)、如图2，若点M在线段AB上，连接OM，作∠OMB的平分线MN交CP于点N，若∠BCD＝n∠MNC，求 $\frac{∠ M O C}{∠ M N C}$ 的值（用含n的式子表示）．

查看试题解析
25. 某化工厂与A、B两地都分别有公路、铁路相连，从A地购买原料运回工厂制成产品运到B地销售．已知3t产品的销售款比4t原料的进货款多20000元，2t产品的销售款比1t原料的进货款多15000元．

(1)、求每吨原料的进货款和产品的销售款分别多少元？

(2)、如表为该化工厂与A、B两地的距离，已知公路运价为1.5元/（t•km），铁路运价为1.2元/（t•km），且这两次运输共支出公路运费15000元，铁路运费97200元，求这批原料比产品多多少吨？

A地
B地
公路段路程（km）
10
20
铁路段路程（km）
120
110

(3)、工厂原计划从A地购买的原料和送往B地的产品一共20t，若要增加at的产品，就要再购买 $\frac{8}{5}$ at的原料，此时产品的销售款与原料的进货款之差不少于66000元，同时满足原料总重量是产品总重量的2倍，求至少需要再购买多少吨的原料？

查看试题解析
26. 定义：在平面直角坐标系中，对于点P（x，y），若点Q坐标为（2m﹣x，﹣y），其中m为常数，我们称点P与点Q是相关点．
例如：当m＝0时，点P（1，2）的相关点Q为（﹣1，﹣2）．

(1)、当m＝1时，点P坐标为（2，3），则它的相关点Q的坐标；

(2)、若点P在y轴上，且它的相关点Q坐标为（m+2，﹣2m）．
①求△OPQ的面积；
②若存在一点A（x，6），使△APQ的面积大于△OPQ的面积，请直接写出x的取值范围 ▲ ；

(3)、若点P（﹣m﹣3，4）和它的相关点Q到y轴的距离中最大值为m+8，求m的值．

查看试题解析

x	16	16.1	16.2	16.3	16.4	16.5	16.6	16.7	16.8	16.9	17
$x^{2}$	256	259.21	262.44	265.69	268.96	272.25	275.56	278.89	282.24	285.61	289

成绩x（分）	频数（人）	百分比
50≤x＜60	12	12%
60≤x＜70	20	a
70≤x＜80	b	c
80≤x＜90	28	28%
90≤x＜100	16	16%

	A地	B地
公路段路程（km）	10	20
铁路段路程（km）	120	110