辽宁省朝阳市建平县2020-2021学年七年级下学期期末数学试题
试卷更新日期：2022-04-15 类型：期末考试
一、单选题
-
1. 以下四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 某红外线遥控器发出的红外线波长为0.00000094m，用科学记数法表示这个数据是（ ）A、9.4×10﹣7m B、9.4×107m C、9.4×10﹣8m D、0.94×10﹣6m3. 下列运算正确的是（ ）A、m2•m3＝m6 B、（m4）2＝m6 C、m3+m3＝2m3 D、（m﹣n）2＝m2﹣n24. 下面各语句中，正确的是（ ）A、相等的角是对顶角 B、同角或等角的余角相等 C、过一点有且只有一条直线与已知直线平行 D、同旁内角互补5. 如图，直线EF分别与直线AB，CD相交于点G，H，已知∠1=∠2=50°，GM平分∠HGB交直线CD于点M，则∠3等于（ ）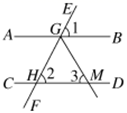
A、60° B、65° C、70° D、130°6. 如图，点A在DE上，AC＝EC，∠1＝∠2＝∠3，则DE等于（ ）
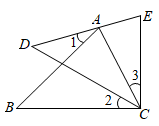A、AB B、BC C、DC D、AE+AC7. 下列说法中，正确说法的个数有（ ）①角是轴对称图形，对称轴是角的平分线；②等腰三角形至少有1条对称轴，至多有3条对称轴；③关于某直线对称的两个三角形一定是全等三角形；④一个锐角和一条边相等的两个直角三角形全等．
A、1个 B、2个 C、3个 D、4个8. 定义：当三角形中一个内角α是另一个内角的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的一个内角为48°，那么这个“特征角”α的度数为（ ）A、48° B、96° C、88°或48° D、48°或96°或88°9. 珠江流域某江段江水流向经过B、C、D三点，拐弯后与原来方向相同．如图，若∠ABC＝120°，∠BCD＝80°，则∠CDE等于（ ）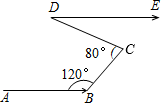
A、20° B、40° C、60° D、80°10. 甲、乙两辆摩托车同时从相距20km的A，B两地出发，相向而行．图中l1 ， l2分别表示甲、乙两辆摩托车到A地的距离s（km）与行驶时间t（h）的函数关系．则下列说法不正确的是（ ）
A、乙摩托车的速度较快 B、经过0.3小时甲摩托车行驶到A，B两地的中点 C、经过0.25小时两摩托车相遇 D、当乙摩托车到达A地时，甲摩托车距离A地
km
二、填空题
-
11. 转动如图的转盘（转盘中各个扇形的面积都相等），当它停止转动时，指针指向标有数字的区域的可能性最小.
12. 如果x+y=2， x2- y2=6，则x-y =.13. 已知等腰三角形的一个内角为80°，则这个等腰三角形的顶角为 ．14. 如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDF，请你添加一个条件，使DE=DF成立．你添加的条件是 ． （不再添加辅助线和字母）
15. 如图，正方形ABCD的边长为6．则图中阴影部分的面积为 ．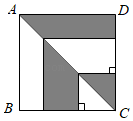
16. 观察下列图形：第1个图形中一共有4个小圆圈，第2个图形中一共有10个小圆圈，第3个图形中一共有18个小圆圈…，按此规律排列，则第n个图形中小圆圈的个数是 ．
三、解答题
-
17. 计算：(1)、﹣2x2y3•（﹣x3y2）；(2)、（π﹣3）0+|﹣5|﹣（﹣）2020×（）2021﹣（﹣1）﹣3 ．18. 把一张长方形（对边平行）纸条按如图所示折叠．判断∠1与∠2相等吗？说明理由．
19.(1)、（x+2y﹣3）（x+2y+3）．(2)、先化简，再求值：[（x+2y）（x﹣2y）﹣（x+4y）2]÷4y，其中x＝5，y＝2．20. 如图，在正方形网格中，每个小正方形的边长都为1，网格中有一个格点三角形△ABC（即三角形的顶点都在格点上）．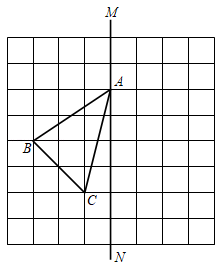
(1)、在图中作出△ABC关于直线MN的对称图形△A′B′C′．(2)、利用网格纸，在MN上找一点P，使得PB+PC的距离最短．（保留痕迹）21. 已知一个纸箱中放有大小相同的10个白球和若干个黄球．从箱中随机地取出一个是白球的概率是 ， 再往箱中放进20个白球，求随机地取出一个黄球的概率．22. 如图，已知AB＝DC，AB∥CD，E、F是AC上两点，且AF＝CE．
(1)、△ABE与△CDF是否全等，并说明理由；(2)、连接BC，若∠CFD＝100°，∠BCE＝30°，求∠CBE的度数．23. 小明家距离学校8千米，今天早晨小明骑车上学途中，自行车突然“爆胎”，恰好路边有便民服务点，几分钟后车修好了，他加快速度骑车到校．我们根据小明的这段经历画了一幅图象，该图描绘了小明行驶路程s与所用时间t之间的函数关系，请根据图象回答下列问题：
(1)、小明骑车行驶了千米时，自行车“爆胎”；修车用了分钟．(2)、修车后小明骑车的速度为每小时千米．(3)、小明离家分钟距家6千米．(4)、如果自行车未“爆胎”，小明一直按修车前速度行驶，那么他比实际情况早到或晚到多少分钟．24. 如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线AP，交CD于点M．
(1)、若∠ACD＝124°，求∠MAB的度数；(2)、若CN⊥AM，垂足为N，试说明△CAN≌△CMN．25. 已知：两个等腰直角三角板△ACB和△DCE（AC＝BC，DC＝CE，∠ACB＝∠DCE＝90°）如图所示摆放，连接AE、BD交于点O．AE与DC交于点M，BD与AC交于点N．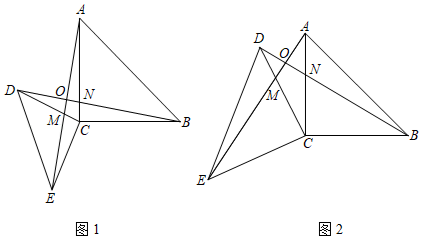
(1)、如图1（两个等腰直角三角板大小不等），试判断AE与BD有何关系并说明理由；(2)、如图2（两个等腰直角三角板大小相等，即AC＝DC），在不添加任何辅助线的情况，请直接写出图2中四对全等的直角三角形．