河南省南阳市六校2021-2022学年高一下学期数学第一次联考试卷
试卷更新日期:2022-04-15 类型:月考试卷
一、单选题
-
1. 计算的结果等于( )A、 B、 C、 D、2. 已知集合 , 下列描述正确的是( )A、 B、 C、 D、以上选项都不对3. 函数的定义域是( )A、 B、 C、 D、4. 已知 , 则的值等于( )A、 B、 C、 D、5. 对于四个函数 , , , , 下列说法错误的是( )A、不是奇函数,最小正周期是 , 没有对称中心 B、是偶函数,最小正周期是 , 有无数多条对称轴 C、不是奇函数,没有周期,只有一条对称轴 D、是偶函数,最小正周期是 , 没有对称中心6. 函数的值域是( )A、 B、 C、 D、7. 铸于明嘉靖十二年的泰山岱庙铁塔,造型质朴雄伟,原有十三级,抗日战争中被日军飞机炸毁,现仅存三级,它的底座是近似圆形的,如图1.我国古代工匠已经知道,将长方体砖块以某个固定的角度相接就可砌出近似圆形的建筑,现存铁塔的底座是用10块一样的长方体砖块砌成的近似圆形的墙面,每块长方体砖块底面较长的边长为1个单位,相邻两块砖之间的夹角固定为36°,如图2,则此近似圆形墙面内部所能容纳最大圆的半径是( )
 A、 B、 C、 D、8. 有以下四种变换方式:
A、 B、 C、 D、8. 有以下四种变换方式:①向右平移个单位长度,再将每个点的横坐标缩短为原来的;②向左平移个单位长度,再将每个点的横坐标伸长为原来的2倍;③每个点的横坐标缩短为原来的 , 再向右平移个单位长度;④每个点的横坐标伸长为原来的2倍,再向左平移个单位长度.
其中能将函数的图象变为函数的图象的是( )
A、①③ B、①④ C、②③ D、②④9. 函数在区间内的图象是( )A、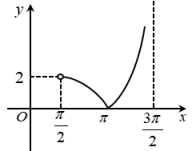 B、
B、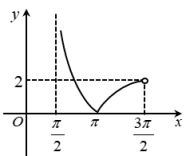 C、
C、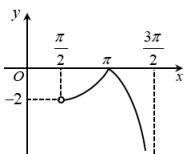 D、
D、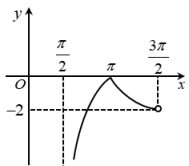 10. 已知一扇形的周长为 , 则当该扇形的面积取得最大时,圆心角大小为( )A、 B、 C、1 D、211. 已知函数 , , 若两函数图象在某一确定区间内共有个交点,则的值分别为( )A、 B、 C、 D、12. 已知 , 则的大小关系是( )A、 B、 C、 D、
10. 已知一扇形的周长为 , 则当该扇形的面积取得最大时,圆心角大小为( )A、 B、 C、1 D、211. 已知函数 , , 若两函数图象在某一确定区间内共有个交点,则的值分别为( )A、 B、 C、 D、12. 已知 , 则的大小关系是( )A、 B、 C、 D、二、填空题
-
13. 已知函数的部分图象如图所示,其中图象最高点和最低点的横坐标分别为和 , 图象与轴交点的纵坐标为 , 则函数的解析式为.
 14. 如图,已知扇环(注:扇环是一个圆环被扇形截得的一部分)中弧长为 , 弧长为 , 线段长为 , 为圆心,则.
14. 如图,已知扇环(注:扇环是一个圆环被扇形截得的一部分)中弧长为 , 弧长为 , 线段长为 , 为圆心,则. 15. 已知函数在区间上不是单调函数,且 , 则的取值范围是.16. 已知表示不超过的最大整数,则函数的零点有个.
15. 已知函数在区间上不是单调函数,且 , 则的取值范围是.16. 已知表示不超过的最大整数,则函数的零点有个.三、解答题
-
17. 已知函数的最大值为1,最小值为 , 最小正周期为.(1)、求函数的解析式;(2)、求函数的单调增区间.18. 如图,以为始边作角与 , 它们的终边分别与单位圆相交于点 , 已知点的坐标为.
 (1)、求的值;(2)、若 , 求的值.19. 已知某半径小于的扇形 , 其周长是 , 面积是.(1)、求该扇形的圆心角的弧度数;(2)、求该扇形中所含弓形面积(注:弓形是指在圆中由弦及其所对的弧组成的图形).20. 已知函数的最小正周期为2,其图象过点.(1)、求的解析式和对称中心;(2)、请指出函数的图象可由的图象经过怎样的变换得到.
(1)、求的值;(2)、若 , 求的值.19. 已知某半径小于的扇形 , 其周长是 , 面积是.(1)、求该扇形的圆心角的弧度数;(2)、求该扇形中所含弓形面积(注:弓形是指在圆中由弦及其所对的弧组成的图形).20. 已知函数的最小正周期为2,其图象过点.(1)、求的解析式和对称中心;(2)、请指出函数的图象可由的图象经过怎样的变换得到.
