浙江省宁波市2022年中考4月模拟考试数学试卷
试卷更新日期：2022-04-15 类型：中考模拟
一、选择题（共10小题，满分40分，每小题4分）
-
1. 同学们，我们是2022届学生，这个数字2022的相反数是（ ）A、2022 B、 C、-2022 D、2. 七巧板是我国的一种传统智力玩具．下列用七巧板拼成的图形中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 下列计算正确的是（ ）A、a2+a2=a4 B、（a2）3=a5 C、(-a2b)3=a6b3 D、(b+2a)(2a-b)=4a2-b24. 如图所示的几何体，它的左视图正确的是（ ）
A、
B、
C、
D、
5. 一组数据，6、4、a、3、2的平均数是5，这组数据的方差为（ ）A、8 B、5 C、 D、36. 在一个不透明的盒子中装有 a 个黑白颜色的球，小明又放入了5个红球，这些球大小相同．若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则 a的值大约为（ ）A、15 B、20 C、25 D、307. 如图， ⊙O为△ABC的外接圆，点 D 在 弧AB上，且 OD⊥AB ．若 ∠A=42°， ∠B=66° ，则 ∠COD 的度数是（ ）
A、132° B、144° C、156° D、168°8. 如图，二次函数y=ax2+bx+c（a≠0） 的图象的对称轴是直线 x=1 ，则以下四个结论中：① abc＞0 ，② 2a+b=0 ，③ 4a+b2＜4ac ，④ 3a+c＜0 ．正确的个数是（ ）
A、1 B、2 C、3 D、49. 如图， △ABC是⊙O的内接三角形，将劣弧AC沿AC折叠后刚好经过弦BC 的中点 D．若 AC=6，∠C=60°，则⊙O的半径长为（ ）
A、 B、 C、 D、10. 如图，大矩形分割成五个小矩形，④号、⑤号均为正方形，其中⑤号正方形边长为1．若②号矩形的长与宽的差为2，则知道哪个小矩形的周长，就一定能算出这个大矩形的面积（ ）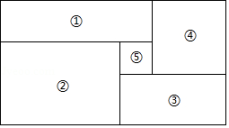
A、①或③ B、② C、④ D、以上选项都可以二、填空题（共6小题，满分30分，每小题5分）
-
11. 函数的自变量x的取值范围是 ．12. 分解因式： 3x2-6x+3= ．13. 已知圆锥的底面圆的半径是2.5，母线长是6，其侧面展开图的面积.14. 在平面直角坐标系xOy 中，已知点 M ， N 的坐标分别为（-1，2）， （2，1） ，若抛物线 y=ax2-x+2(a＞0） 与线段MN有两个不同的交点，则a的取值范围是 ．15. 如图，在△ABC 中， AB=AC ，底边BC 在x轴正半轴上，点 A在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE=AC ，若双曲线经过点E，则△BCD的面积为 ．
16. 如图，在Rt△ABC中，AB=4，BC=3 ，点D在斜边AB 上，连接CD把△ACD沿直线CD 翻折，使点A落在同一平面内的点A'处．当A'D与Rt△ABC的直角边垂直时， AD的长为 ．
三、解答题（共8小题，满分80分）
-
17. 计算：(1)、2sin60°-|1-|-（-1）2021-2-2 ．(2)、先化简，再求值： ， 从1，2，3这三个数中选择一个你认为适合的x代入求值．18. 某中学对全校九年级学生进行了一次数学模拟考试，并随机抽取了部分学生的测试成绩作为样本进行分析，绘制成了如下两幅不完整的统计图，请根据图中所给信息，解答下列问题：
第18题图
(1)、将条形统计图补充完整；(2)、在扇形统计图中，表示成绩类别为“优”的扇形所对应的圆心角是度；(3)、学校九年级共有600人参加了这次数学考试，估算该校九年级共有多少名学生的数学成绩类别可以达到“中”（不包括“中” ) 以上？(4)、学校准备从成绩进步最大的3名同学(1名男生、2名女生）中随机选取2名同学介绍学习经验，则选出的同学恰好是2名女生的概率是 ．19. 图1，图2都是由边长为1的小等边三角形构成的网格， △ABC 为格点三角形．请仅用无刻度直尺在网格中完成下列画图．
(1)、在图1中，画出△ABC中AB边上的中线CM ；(2)、在图2中，画出∠APC，使∠APC=∠ABC，且点P是格点（画出一个即可）．20. 已知抛物线y=ax2-2ax-8（a≠0）经过点（-2，0）．(1)、求抛物线的函数表达式和顶点坐标．(2)、直线l交抛物线于点a（-4，m）， B（n，7） ， n为正数．若点P在抛物线上且在直线l下方（不与点A，B重合），分别求出点P横坐标与纵坐标的取值范围．21. 如图1，是一种自卸货车，如图2是货箱的示意图，货箱是一个底边AB水平的矩形，AB=8米，BC=2米，前端挡板高DE=0.5米，卸货时，货箱底边AB的仰角α=37° (如图3)， 底端B离地面的距离为13米，求此时档板最高点离地面的高度. (精确到0.1米，参考值：sin37° ≈0.60， cos37° ≈0.80，tan37°≈0.75)
22. 小张骑自行车匀速从甲地到乙地，在途中休息了一段时间后，仍按原速行驶．他距乙地的距离与时间的关系如图中折线所示，小李骑摩托车匀速从乙地到甲地，比小张晚出发一段时间，他距乙地的距离与时间的关系如图中线段 AB 所示．
(1)、小李到达甲地后，再经过小时小张到达乙地；小张骑自行车的速度是千米/ 小时．(2)、小张出发几小时与小李相距15千米？(3)、若小李想在小张休息期间与他相遇，则他出发的时间 x 应在什么范围？（直接写出答案）23.
(1)、【基础巩固】如图①，∠ABC=∠ACD=∠CED=α，求证：△ABC∽△CED .
(2)、【尝试应用】如图②，在菱形ABCD中，∠A=60°，点E， F分别为边AD， AB上两点，将菱形4BCD沿EF翻折，点A恰好落在对角线DB上的点P处，若PD=2PB，求的值.
(3)、【拓展提高】如图③，在矩形ABCD中，点P是AD边上一点，连接PB、PC，若PA=2， PD=4，∠BPC= 120°，求AB的长.
24. 如图1，锐角△ABD（AB＜AD）内接于⊙M，弦AC⊥BD于点O。已知⊙M半径为5，且AC=BD.
(1)、求∠ADB的度数；(2)、若△ABO的面积为 ， 求 BD 的长；(3)、如图2，在(2)的条件下，点E，F分别在OD，MD上，连接EF， ME，若∠DEF=∠DAB，求△MEF面积的最大值.