浙江省温州市2022年九年级下学期数学3月第一次模拟试卷

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 2022年，温州市委、市政府决定发放新一轮消费券1200000000元，数据1200000000用科学记数法表示为（）

A、 $12 \times 1 0^{8}$ B、 $1.2 \times 1 0^{8}$ C、 $1.2 \times 1 0^{9}$ D、 $0.12 \times 1 0^{10}$

查看试题解析
3. 如图是由一个长方体和一个圆锥组成的几何体，它的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $2 x - x = 2$ B、 $x^{6} \div x^{2} = x^{3}$ C、 ${(x + y)}^{2} = x^{2} + y^{2}$ D、 ${(- x y^{3})}^{2} = x^{2} y^{6}$

查看试题解析
5. 如图，为某套餐营养成分的扇形统计图，一份套餐中蛋白质有70克，则碳水化合物含量为（）

A、35克 B、70克 C、105克 D、140克

查看试题解析
6. 若扇形的圆心角为45°，半径为6，则扇形的弧长为（）

A、 $\frac{9}{8} π$ B、 $\frac{3}{4} π$ C、 $\frac{3}{2} π$ D、 $\frac{9}{2} π$

查看试题解析
7. 如图，四边形ABCD与四边形AEFG是位似图形，位似比为3∶2.若EF=6，则BC的长为（）

A、8 B、9 C、10 D、15

查看试题解析
8. 同学聚餐预定的酒席价格为2400元，但有两位同学因时间冲突缺席，若总费用由实际参加的人平均分摊，则每人比原来多支付40元，设原来有x人参加聚餐，由题意可列方程（）

A、 $\frac{2400}{x + 2} = \frac{2400}{x} + 40$ B、 $\frac{2400}{x + 40} + 40 = \frac{2400}{x}$ C、 $\frac{2400}{x} = \frac{2400}{x - 2} + 40$ D、 $\frac{2400}{x} + 40 = \frac{2400}{x - 2}$

查看试题解析
9. 图1是2002年世界数学大会（ICM）的会徽，其主体图案（如图2）是由四个全等的直角三角形组成的四边形.若 $∠ A B C = α$ ， AB＝1，则CD的长为（）

A、 $s i n α - c o s α$ B、 $\frac{1}{s i n α} - \frac{1}{c o s α}$ C、 $c o s α - s i n α$ D、 $\frac{1}{c o s α} - \frac{1}{s i n α}$

查看试题解析
10. 在平面直角坐标系中，已知点 $A (m^{2} - 1 ， n)$ ， $B (m^{2} ， n - 1)$ ，下列y关于x的函数中，函数图象可能同时经过A，B两点的是（）

A、 $y = 3 x + c$ B、 $y = a (x - 1) (a \neq 0)$ C、 $y = 2 x^{2} + 4 x + c$ D、 $y = - \frac{k^{2} + 1}{x}$

查看试题解析

二、填空题

11. 若 $| p + 4 | = 0$ ，则 $p$ =.

查看试题解析
12. 不等式组 ${\begin{array}{l} 2 x + 9 \geq 3 \\ \frac{4 - x}{3} > 1 \end{array}$ 的解为.

查看试题解析
13. 在一个不透明的袋中装有6个只有颜色不同的球，其中3个红球、2个黄球和1个白球.从袋中随机摸出一个球，是黄球的概率为.

查看试题解析
14. 某电梯中一面镜子正对楼层显示屏，显示屏中显示的是电梯所在楼层号和电梯运行方向.当电梯中镜子如图显示时，电梯所在楼层号为.

查看试题解析
15. 如图，在平面直角坐标系中，菱形OABC的边OA在x轴正半轴上，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过顶点C和对角线OB的中点D.作 $C E ∥ O B$ 交y轴于点E.若 $△ A D E$ 的面积为12，则k的值为.

查看试题解析
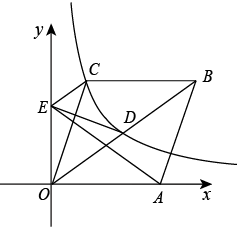16. 图1是一种木质投石机模型，其示意图如图2所示.已知 $A B = A C$ ， $B D = 4$ cm， $B C = 8$ cm，木架高 $A G = 8$ cm.按压点F旋转至点 $F^{'}$ ，抛杆EF绕点A旋转至 $E^{'} F^{'}$ ，弹绳DE随之拉伸至 $D E^{'}$ ，测得 $∠ C D E^{'} = ∠ B A E^{'} = 90 °$ ，则抛杆EF的长为cm.若弹绳自然状态时，点A，E，D在同一直线上，则此次旋转后弹绳被拉长的长度 $D E^{'} - D E$ 为cm.

查看试题解析

三、解答题

17.

(1)、计算： $6 \div (- 3) + \sqrt{4} - 8 \times 2^{- 2}$ .

(2)、化简： $\frac{2 x}{x^{2} - 4} - \frac{1}{x - 2}$ .

查看试题解析
18. 如图，在五边形ABCDE中，∠B＝∠E＝90°，BC＝DE，连结AC，AD，∠ACD＝∠ADC.

(1)、求证： $△ A B C ≌ △ A E D$ .

(2)、若 $A C ∥ D E$ ， ∠ACD＝65°，求∠BAE的度数.

查看试题解析
19. 小皮的寒假社会实践任务是调查某车间每个工人的日均生产能力，他想用条形统计图来反映这个调查成果，并进行数据分析.

(1)、以下排乱的统计步骤：①将每个工人的日均生产件数整理成统计表；②通过访谈记录下每个工人的日均生产件数；③利用统计图分析该工厂数据；④按统计表的数据绘制成统计图.正确的统计步骤应该是.

(2)、小皮按照正确统计步骤绘制出如下统计图.

①求出这16名工人日均生产件数的平均数、中位数、众数.

②若要使超过75%的工人都能完成任务，应选①中的哪个统计量作为日生产件数的定额？

查看试题解析
20. 如图，在 $7 \times 5$ 的方格中， $△ A B C$ 的顶点均在格点上.请按要求画格点线段EF（端点在格点上），且EF分别交线段AB，AC于点G，H.

(1)、在图1中作出∠AHG＝∠C.

(2)、在图2中作出∠AGH＝∠C.

查看试题解析
21. 已知抛物线 $y = x^{2} + b x + c$ 经过 $(0 ， 8)$ ， $(4 ， 0)$ 两点.

(1)、求抛物线的表达式及其顶点坐标.

(2)、点 $A (a ， y_{1})$ ， $B (6 - a ， y_{2})$ 都在抛物线上， $S = y_{1} + 3 y_{2}$ ，当 $- 1 \leq a \leq 6$ 时，求S的取值范围.

查看试题解析
22. 如图，四边形ABCD内接于 $⊙ O$ ， $A E ⊥ C B$ 的延长线于点E，连结AC，BD，AB平分 $∠ E B D$ .

(1)、求证：AC＝AD.

(2)、当B为弧AC的中点，BC＝3BE，AD＝6时，求CD的长.

查看试题解析

23. 某产家在甲、乙工厂生产同一商品，并将其分几天运往A地240吨，B地260吨，表1是两个工厂的商品记录，表2为该商品的运费标准（m，n为常数）.

表1

时间	甲工厂商品记录	乙工厂商品记录	甲、乙两工厂总运费
第1天	生产商品200吨	生产商品300吨
第2天	运往A地30吨	运往A地10吨，运往B地20吨	1230元
第3天	运往B地20吨	运往B地40吨	1460元

甲乙两厂往A，B地运输该商品的运费标准（单位：元/吨）

表2

目的地

工厂

甲

乙

(1)、求m，n的值.

(2)、若运费标准不变，要使剩余商品按要求运往A，B两地，且总运费最少，请给出剩余商品的运输方案.

(3)、若从第4天开始，运输公司将甲工厂往B地的运费提高a元/吨，乙工厂往B地的运费降低a元/吨，其中a为正整数，若可用不超过7150元的费用按要求完成剩余商品的运输，求a的最小值.

查看试题解析

24. 如图，在矩形ABCD中，AB＝4，BC＝6，点E，F分别在边AD，CD上，且∠ABE＝∠CBF，延长BE交CD的延长线于点G，H为BG中点，连结CH分别交BF，AD于点M，N.

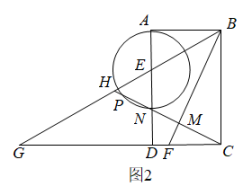(1)、求证： $B F ⊥ C H$ .

(2)、当FG＝9时.
①求 $t a n ∠ F B G$ 的值.
②在线段CH上取点P，以E为圆心，EP为半径作 $⊙ E$ （如图），当 $⊙ E$ 与四边形ABMN某一边所在直线相切时，求所有满足条件的HP的长.

查看试题解析