浙江省温州市2022年初中学业水平适应性考试数学试卷（二）

试卷更新日期：2022-04-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 已知2x=3y（y≠0），则下面结论成立的是（）

A、 $\frac{x}{y}$ = $\frac{3}{2}$ B、 $\frac{x}{3}$ = $\frac{2}{y}$ C、 $\frac{x}{y}$ = $\frac{2}{3}$ D、 $\frac{x}{2}$ = $\frac{y}{3}$

查看试题解析
2. 如图，由几个小正方体组成的立体图形的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 太阳与地球的平均距离大约是150000000 km，其中数150000000用科学记数法表示为（）

A、1.5×10⁸ B、15×10⁷ C、1.5×10⁷ D、0.15×10⁹

查看试题解析
4. 某校950名七年级学生参加跳绳测试，随机抽取部分学生成绩并绘制频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，若校方规定次数达到130次（包括130次）的成绩为“优良”，则该校成绩“优良”的学生人数约为（）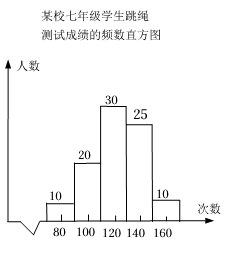

A、35 B、65 C、350 D、650

查看试题解析
5. 若扇形的圆心角为60°，半径为4，则该扇形的面积为（）

A、 $\frac{2}{3} π$ B、 $\frac{4}{3} π$ C、 $\frac{8}{3} π$ D、 $\frac{16}{3} π$

查看试题解析
6. 某口罩厂平均每天可生产20万只口罩，厂家引进新技术，经过连续两次增速后，平均每天可生产30万只.若两次的增长率都为x，则可得方程（）

A、 $(20 + x)^{2} = 30$ B、 $20 (1 + x)^{2} = 30$ C、 $20 (1 + 2 x) = 30$ D、 $20 (1 + x) + 20 (1 + x)^{2} = 30$

查看试题解析
7. 把直尺、三角尺和圆形螺母按如图所示的方式放置于桌面上，AB与螺母相切，D为螺母与桌面的切点，∠CAB=60°.若量出AD=6cm，则圆形螺母的外直径是（）

A、 $12 \sqrt{3}$ cm B、12cm C、 $6 \sqrt{3}$ cm D、 $4 \sqrt{3}$ cm

查看试题解析
8. 二次函数 $y = a x^{2} + b x + c$ 的若干组函数值如表所示：
$x$
...
-5
-4
0
1
2
5
...
$y$
...
$m$
2
4
2
-1
-16
...
则 $m$ 的值为（）

A、4 B、0 C、-1 D、-16

查看试题解析
9. 一个长方体木箱放置在斜面上，其端点A落在水平地面上，相关数据如图所示，则木箱端点C距地面m的高度是（）

A、 $a \cdot c o s α + b \cdot s i n α$ B、 $a \cdot s i n α + b \cdot c o s α$ C、 $a \cdot s i n α + b \cdot s i n α$ D、 $a \cdot c o s α + b \cdot c o s α$

查看试题解析
10. 古希腊数学家帕普斯利用反比例函数的图象和性质解决了三等分角问题，其方法如下：如图，在直角坐标系中，锐角 $∠ A O B$ 的边OB在x轴正半轴上，边OA与 $y = \frac{k}{x} (k > 0)$ 的图象交于点A，以A为圆心，2OA为半径作圆弧交函数图象于点C，取AC的中点P，则 $∠ B O P = \frac{1}{3} ∠ A O B$ .若 $6 O A = 5 O P = 30$ ，则k的值为（）

A、 $\frac{21}{5}$ B、 $\frac{22}{5}$ C、 $\frac{19 \sqrt{5}}{10}$ D、 $\frac{117}{10}$

查看试题解析

二、填空题

11. 分解因式： $m^{2} - 4 m =$ .

查看试题解析
12. 某商场举办有奖销售活动，每张奖券获奖的可能性相同.以每10000张奖券为一个开奖单位，设一等奖100名，二等奖300名，三等奖600名，则1张奖券中奖的概率为.

查看试题解析
13. 如图，在菱形ABCD中， $D E ⊥ A B$ ， $D F ⊥ B C$ ，垂足分别为点E，F.若 $∠ A D E + ∠ C D F = 80 °$ ，则 $∠ E D F$ 等于度.

查看试题解析
14. 关于 $x$ 的方程 $2 a x = (a + 1) x + 6$ 的解是 $x = 1$ ，现给出另一个关于 $x$ 的方程 $2 a (x - 1) = (a + 1) (x - 1) + 6$ ，则它的解是.

查看试题解析
15. 如图，墙上有一个矩形门洞ABCD，现要将其改为直径为4m的圆弧形，圆弧经过点B，C分别交AB，CD于E，F.若 $A B = 4$ m， $B C = 2$ m，则要打掉的墙体面积为 $m^{2}$ .

查看试题解析
16. 我们知道，勾股定理反映了直角三角形三条边的关系： $a^{2} + b^{2} = c^{2}$ ，而 $a^{2}$ ， $b^{2}$ ， $c^{2}$ 又可以看成是以a，b，c为边长的正方形的面积.如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = a$ ， $B C = b$ ， O为AB的中点，分别以AC，BC为边向 $△ A B C$ 外作正方形ACFG，BCED，连接OF，EF，OE，则 $△ O E F$ 的面积为（用含a，b的代数式表示），若 $a + b = 8$ ，则 $△ O E F$ 的面积为.

查看试题解析

三、解答题

17.

(1)、计算： $| - 3 | + {(+ 3)}^{0} - 12$ .

(2)、化简： $(x - 3 y)^{2} - x (x + 6 y)$ .

查看试题解析
18. 如图，四边形 $A B C D$ 中， $A D / / B C$ ， E为 $C D$ 的中点，连结 $B E$ 并延长交 $A D$ 的延长线于点F.

(1)、求证： $△ B C E ≌ △ F D E$ ；

(2)、连结 $A E$ ，当 $A E ⊥ B F ， B C = 2 ， A D = 1$ 时，求 $A B$ 的长.

查看试题解析
19. 某校策划了一次有关党的知识竞赛，每班参加比赛的人数相同，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为100分，90分，80分，70分，学校将九年级一班和二班的成绩进行整理并绘制成如下统计图.
请你根据以上提供的信息解答下列问题：

(1)、此次竞赛中，一班成绩在C级以上（包括C级）的人数为人.

(2)、请你根据平均数、众数、中位数等统计知识，综合阐述哪个班整体水平较高，可以评为一等奖？

查看试题解析
20. 如图，是 $8 \times 8$ 的方格纸，线段AB的两个端点分别落在格点上，请按照要求画图：

(1)、在图1中画一个格点四边形APBQ，且AB与PQ互相平分.

(2)、在图2中画一个以AB为中位线的格点 $△ D E F$ .

查看试题解析
21. 已知抛物线 $y = - 2 x^{2} + b x + c$ 经过点 $(- 1 ， 0)$ ， $(2 ， 6)$ .

(1)、求 $b$ ， $c$ 的值.

(2)、已知 $k$ 为正数，当 $0 < x ⩽ 1 + k$ 时， $y$ 的最大值和最小值分别为 $m$ ， $n$ ，且 $m + n = 14$ ，求 $k$ 的值.

查看试题解析
22. 如图，在菱形ABCD中，点E，F分别在AD，CD边上，且 $D E = D F$ ，连接EF并延长EF交BC的延长线于点G.

(1)、求证： $∠ G = \frac{1}{2} ∠ A$ .

(2)、连接BE，BF，当 $∠ E B F = ∠ A$ ， $t a n ∠ G = \frac{1}{2}$ 时，求 $\frac{D E}{C G}$ 的值.

查看试题解析

23. 某中学为筹备校庆，准备印制一批纪念册.该纪念册每册需要10张纸，其中4张彩色页，6张黑白页.印刷该纪念册的总费用由制版费和印刷费两部分组成，制版费与印数无关，价格为2200元，印刷费与印数的关系见表.

印数a（千册）	$0 ⩽ a < 5$	$a ⩾ 5$
彩色（元/张）	2.1	2
黑白（元/张）	0.8	0.5

(1)、若印制2千册，则共需多少元？

(2)、该校先印制了x千册纪念册，后发现统计失误，补印了y（

y ⩾ 5

）千册纪念册，且补印时无需再次缴纳制版费，学校发现补印的单册造价便宜了，但两次缴纳费用恰好相同.

①用含x的代数式表示y.

②若该校没有统计错误，一次性打印全部纪念册，最少需要多少钱？

查看试题解析

24. 如图，已知AB是⊙O的直径，P是半径OB上一点，作弦 $C D ⊥ A B$ 交⊙O于点C，D，其中 $C D = 8$ ， $A B = 10$ .E是 $\overset{⌢}{A D}$ 上一点，延长AE交CD的延长线于点F，延长BD交EF于点G，连结DE.

(1)、求证： $∠ A E C = ∠ D E F$ .

(2)、连结BC，当四边形BCEG中有一组对边平行时，求DE的长.

(3)、当 $t a n F = \frac{2}{3}$ 时，求 $\frac{D E}{A E}$ 的值.

查看试题解析

$x$	...	-5	-4	0	1	2	5	...
$y$	...	$m$	2	4	2	-1	-16	...