江苏省扬州市2021-2022学年八年级下学期期中数学试卷
试卷更新日期：2022-04-15 类型：期中考试
一、单选题
-
1. 最近北京2022年冬奥会的吉祥物“冰墩墩”成为了互联网的“顶流”，他呆萌的形象受到了人们的青睐，结合你所学知识，从下列四个选项中选出能够和如图的图片成中心对称的是（ ）
A、
B、
C、
D、
2. 下列调查中，适宜采用全面调查方式的是（ ）A、考察某市市民保护海洋的意识 B、了解一批手机电池的使用寿命 C、调查某品牌食品的色素含量是否超标 D、了解全班学生参加社会实践活动的情况3. 今年某市有3万名学生参加了关于“你喜爱的一项体育运动”的问卷调查，从中抽取3000名学生的调查结果进行统计分析，以下说法错误的是（ ）A、3万名学生的问卷调查结果是总体 B、3000名学生的问卷调查结果是样本 C、3000名学生是样本容量 D、每一名学生的问卷调查结果是个体4. 下列成语描述的事件是随机事件的是（ ）A、海枯石烂 B、画饼充饥 C、瓜熟蒂落 D、守株待兔5. 下列条件中，能判定四边形是平行四边形的条件是（ ）A、一组对边平行，另一组对边相等 B、一组对边平行，一组对角相等 C、一组对边平行，一组邻角互补 D、一组对边相等，一组邻角相等6. 如图，在平行四边形ABCD中，AB＝5，BC＝8，∠ABC和∠BCD的角平分线分别交AD于点E和F，若BE＝6，则CF＝（ ）
A、6 B、8 C、10 D、137. 如图，△ABC是等边三角形，P是三角形内一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为24，则PD+PE+PF＝（ ）
A、8 B、9 C、12 D、158. 如图，点P为▱ABCD外一点，连接PA、PB、PC、PD，若△APB的面积为18，△APD的面积为5，则△APC的面积为（ ）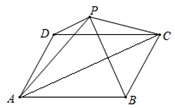
A、10 B、13 C、18 D、20二、填空题
-
9. 若要制作统计图来反映某品牌奶粉中蛋白质、钙、维生素糖和其他物质含量的百分比，最适当的统计图是统计图.（填“折线”、“条形”或“扇形”）10. 一个样本有10个数据：52，51，49，50，47，48，50，51，48，53，如果组距为1.3，则应分成 组.11. 有60个数据，共分成4组，第1、2组的频数分别为25、19，第4组的频率是0.15，则第3组的频数是.12. 用反证法证明命题“一个三角形中不能有两个角是直角”第一步应假设13. 如图，▱ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为.
14. 在平面直角坐标系中，▱ABCD的顶点A、B、C的坐标分别是（0，2）、（﹣3，﹣4）、（2，﹣4），则顶点D的坐标是 .15. 如图，在 中， 、 是对角线 上两点， ， ， ，则 的大小为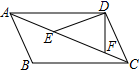
16. 如图，在△ABC中，∠ACB＝90°，D为AB边上一点，连接CD，E为CD中点，连接BE并延长至点F，使得EF＝EB，连接DF交AC于点G，连接CF.若∠A＝30°，BC＝3，CF＝4，则CD＝.
17. 如图，△ABC中，∠B＝30°，∠ACB＝90°，AB＝2，D在BC上，将线段AD绕点A逆时针旋转60°得AP，则CP的最小值为.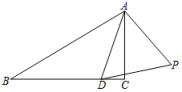
18. 如图，在四边形ABCD中，AD＝4，CD＝3，∠ABC＝∠ACB＝∠ADC＝45°，则BD的长为.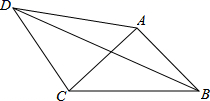
三、解答题
-
19. 如图，已知△ABC的三个顶点的坐标分别为A（﹣3，0），B（﹣5，3），C（﹣1，1）.
⑴画出△ABC关于原点O成中心对称的图形；
⑵P（a，b）是△ABC的AC边上一点，将△ABC平移后点P的对称点 ， 请画出平移后的；⑶若和关于某一点成中心对称，则对称中心的坐标为 ▲ .
20. 新冠肺炎疫情期间，我市防控指挥部想了解自8月1日至8月底各学校教职工介入志愿服务的情况，在全市各学校中随机调查了部分介入志愿者服务的教职工，对他们的志愿服务时间（小时）进行统计，A：0＜x≤30；B：30＜x≤60；C：60＜x≤90；D：90＜x≤120；整理并绘制成两幅不完整的统计图，请回答下列问题：
(1)、这次被抽取的教职工共有人，扇形统计图中，“D：90＜x≤120”所占圆心角的度数是 °；(2)、请你将条形统计图补充完整，并在图上标明相应的数据；(3)、若该市共有3000名教职工参与志愿服务，那么志愿服务时间多于60小时的教职工大约有多少人？21. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小明做摸球试验，他将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是实验中的一组统计数据：摸球的次数n
100
200
300
500
800
1000
3000
摸到白球的次数m
63
124
178
302
481
599
1803
摸到白球的频率
0.63
0.62
0.593
a
0.601
0.599
b
(1)、计算：；；(2)、请估计：当n很大时，摸到白球的频率将会接近 ；（精确到0.1）(3)、求不透明的盒子里黑、白两种颜色的球各有多少个？22. 在四边形ABCD中，有下列条件：①AB∥CD，②∠A＝∠C，③AD＝BC，④∠B＝∠D.从中选择两个条件能够使四边形ABCD成为平行四边形（不添加任何辅助线），请写出所有符合的组合：（用序号表示）(1)、；(2)、选择其中一种组合进行证明.23. 如图，点E、F在线段BC上，AB＝CD，BE＝CF且∠B＝∠C.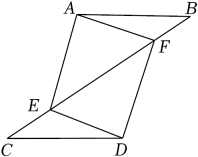
(1)、求证：△ABF≌△DCE；(2)、请猜想四边形AEDF的形状，并加以证明.24. 中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某区若干名中学生家长对这种现象的态度（态度分为：A.无所谓；B.基本赞成；C.赞成：D.反对）.并将调查结果绘制成折线统计图1和扇形统计图2（不完整）.请根据图中提供的信息，解答下列问题.
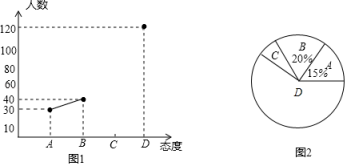(1)、此次抽样调查中，共调查了名中学生家长；(2)、扇形统计图中，表示A类型的扇形圆心角的度数为.(3)、先求出C类型的人数，然后将图1中的折线图补充完整.(4)、根据抽样调查结果，请你估计该区18000名中学生家长中有多少名家长持反对态度？25. 如图，平行四边形ABCD的对角线AC，BD相交于О点，于E点，于F.
(1)、求证：四边形DEBF为平行四边形；(2)、若 ， ， ， 求的面积.26. 【教材呈现】下图是华师版八年级下册数学教材第77页的部分内容.平行四边形的性质定理3：行四边形的对角线互相平分。
我们可以用演绎推理证明这个结论。
已知：如图，的对角线AC和BD相交于点O。
求证：OA=OC，OB=OD。
(1)、请根据教材中的分析，结合图1写出“平行四边形的对角线互相平分”这一性质的完整的证明过程.证明：
(2)、【性质应用】
如图2，的对角线相交于点 ， 过点且与分别相交于点 ，
求证：；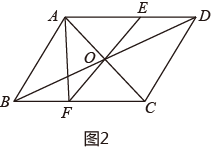
(3)、连结 ， 若 ， 周长是 ， 则的周长是.27. 如图
(1)、问题发现：如图1，△ACB和△DCE均为等边三角形，当△DCE旋转至点A，D，E在同一直线上，连接BE.则：
①∠AEB的度数为°；
②线段AD、BE之间的数量关系是.
(2)、拓展研究：如图2，△ACB和△DCE均为等腰三角形，且∠ACB＝∠DCE＝90°，点 A、D、E在同一直线上，若AD＝a，AE＝b，AB＝c，求a、b、c之间的数量关系.
(3)、探究发现：图1中的△ACB和△DCE，在△DCE旋转过程中，当点A，D，E不在同一直线上时，设直线AD与BE相交于点O，试在备用图中探索∠AOE的度数，直接写出结果，不必说明理由.
28. 如图，在平面直角坐标系中，已知直线PA是一次函数y＝x+m（m＞0）的图象，直线PB是一次函数y＝﹣3x+n（n＞m）的图象，点P是两直线的交点，点A、B、C、Q分别是两条直线与坐标轴的交点.
(1)、用m、n分别表示点A、B、P的坐标及∠PAB的度数；(2)、若四边形PQOB的面积是 ， 且 ， 试求点P的坐标，并求出直线PA与PB的函数表达式；(3)、在（2）的条件下，是否存在一点D，使以A、B、P、D为顶点的四边形是平行四边形？若存在，求出点D的坐标；若不存在，请说明理由.