江苏省扬州市2021-2022年九年级下学期期中数学试卷

试卷更新日期：2022-04-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中是一元二次方程的是（）

A、2x﹣1＝0 B、 $\frac{3}{x} + x = 5$ C、x+y＝6 D、x²﹣2x﹣3＝0

查看试题解析
2. 下列说法中，正确的是（）

A、“任意画一个多边形，其内角和是360°”是必然事件 B、“如果a²＝b² ，那么a＝b”是必然事件 C、可能性是50%的事件，是指在两次试验中一定有一次会发生 D、“从一副扑克牌（含大小王）中抽一张，恰好是红桃”是随机事件

查看试题解析
3. 某学校足球队23人年龄情况如下表：

年龄/岁

12

13

14

15

16

人数

1

3

6

8

5

则下列结论正确的是（）

A、极差为3 B、众数为15 C、中位数为14 D、平均数为14

查看试题解析
4. 如图，⊙O是△ABC的外接圆，直径BD长为4，sin∠BAC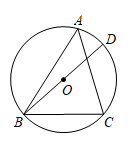＝ $\frac{3}{4}$ ，则BC的长为（）

A、 $\frac{5}{2}$ B、3 C、 $\sqrt{7}$ D、 $\sqrt{11}$

查看试题解析
5. 如图，在△ABC中，∠ACB＝2∠B，CD平分∠ACB，AD＝2，BD＝3，则AC的长为（）

A、3 B、 $\sqrt{10}$ C、4 D、 $2 \sqrt{3}$

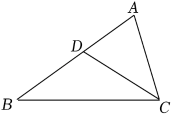查看试题解析
6. 若实数x、y满足2x²﹣6x+y＝0，则x²+y+2x的最大值是（）

A、14 B、15 C、16 D、17

查看试题解析

二、填空题

7. 如图，已知 $l_{1} / / l_{2} / / l_{3}$ ，如果 $A B ： B C = 2 ： 3$ ， $D E = 4$ ，则 $E F$ 的长是.

查看试题解析
8. 若 $⊙ O$ 的半径为5cm，点 $A$ 到圆心 $O$ 的距离为4cm，那么点 $A$ 与 $⊙ O$ 的位置关系是.

查看试题解析
9. 某一学期，小华的数学平时成绩为80分，期中成绩为90分，期末成绩为85分，若平时成绩、期中成绩、期末成绩按3：3：4计算平均成绩，则小华的平均成绩是分.

查看试题解析
10. 已知圆锥的母线长5，底面半径为3，则圆锥的侧面积为．

查看试题解析
11. 如图，已知斜坡AC的坡度i＝1：2，小明沿斜坡AC从点A行进10m至点B，在这个过程中小明升高 m.

查看试题解析
12. 如果方程mx²+2x+1＝0有两个不相等的实数根，那么m的取值范围是 .

查看试题解析
13. 校运动会铅球比赛时，小林推出的铅球行进的高度y（米）与水平距离x（米）满足关系式 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则小林这次铅球推出的距离是米.

查看试题解析
14. 如图，A、B、C均为正十二边形的顶点，则∠ACB＝°

查看试题解析
15. 如图，身高1.8米的轩轩从一盏路灯下的B处向前走了4米到达点C处时，发现自己在地面上的影子CE长与他的身高一样，则路灯的高AB为米.

查看试题解析
16. 如图，点D是△ABC边BC上的一点，且 $\frac{B D}{D C} = \frac{3}{4}$ ，点E是AD的中点，连接BE并延长交AC于点F，则 $\frac{A F}{F C}$ 的值为.

查看试题解析
17. 如图，已知正方形ABCD的边长为4，点E是正方形内部一点，连接BE，CE，且∠ABE＝∠BCE，点F是AB边上一动点，连接FD，FE，则FD+FE的长度最小值为.

查看试题解析

三、解答题

18. 给出下列函数：①y＝﹣3x+2；②y＝ $\frac{3}{x}$ ；③y＝2x²；④y＝﹣5(x﹣1)² ，上述函数中满足“当x＞1时，函数值y随自变量x增大而增大”的是（）

A、① B、② C、③ D、④

查看试题解析
19.

(1)、解方程：x²﹣2x＝99；

(2)、计算： $\sqrt{27} - 2 c o s 30 ° + (\frac{1}{2})^{- 2} - | 1 - \sqrt{3} |$ .

查看试题解析
20. 如图所示，在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A，B，C在小正方形的顶点上.将△ABC向下平移2个单位得到△A₁B₁C₁ ，然后将△A₁B₁C₁绕点C₁顺时针旋转90°得到△A₂B₂C₁.

(1)、在网格中画出△A₁B₁C₁和△A₂B₂C₁；

(2)、计算线段A₁C₁在变换到A₂C₁的过程中扫过区域的面积.

查看试题解析
21. 九年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制了如下两幅不完整的统计图，请根据图中所给信息解答下列问题：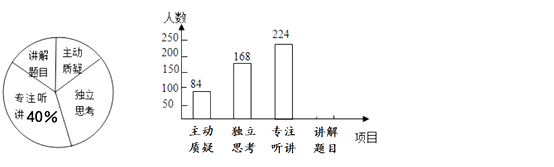

(1)、在这次评价中，一共抽查了名学生；

(2)、请将条形图补充完整；

(3)、如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？

查看试题解析
22. 小倩一家准备本周末出去踏青，他们想在扬州的几个景点中进行选择.
A：瘦西湖；B：个园；C：何园；D：茱萸湾

(1)、如果他们只去一个景点，那么选中瘦西湖的概率为；

(2)、如果他们要去两个景点，那么同时选中个园、何园的概率是多少？请用画树状图或列表法加以解决.

查看试题解析
23. 2022年北京冬奥会吉祥物“冰墩墩”意喻敦厚、健康、活泼、可爱，象征着冬奥会运动员强壮的身体、坚韧的意志和鼓舞人心的奥林匹克精神.随着北京冬奥会开幕日的临近，某特许零售店“冰墩墩”的销售日益火爆.据统计，该店2021年10月的销量为3万件，2021年12月的销量为3.63万件.

(1)、求该店“冰墩墩”销量的月平均增长率；

(2)、假设该店“冰墩墩”销量的月平均增长率保持不变，则2022年1月“冰墩墩”的销量有没有超过4万件？请利用计算说明.

查看试题解析
24. 扬州中国大运河博物馆坐落于扬州三湾古运河畔，大运河博物馆整体由大运塔和博物馆主体两部分组成.周末汐汐和父母去大运河博物馆游玩，看到大运塔时觉得非常宏伟，想知道它的高度.于是汐汐走到点C处，测得此时塔尖A的仰角是37°，向前走了40米至点E处，测得此时塔尖A的仰角是45°，已知汐汐的眼睛离地面高度是1.2米，请聪明的你帮她求出塔AB的高度.（参考数据：sin37°≈ $\frac{3}{5}$ ， cos37°≈ $\frac{4}{5}$ ， tan37°≈ $\frac{3}{4}$ ）

查看试题解析
25. 如图，AB为⊙O的直径，点C在⊙O 上，点P是直径AB上的一点，（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q．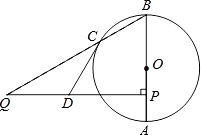

(1)、点D在线段PQ上，且DQ=DC．求证：CD是⊙O的切线；

(2)、若sin∠Q= $\frac{3}{5}$ ，BP=6，AP=2，求QC的长．

查看试题解析
26. 某商场经营某种品牌童装，进货时的单价是40元，根据市场调查，当销售单价是60元时，每天销售量是200件，销售单价每降低0.5元，就可多售出10件.

(1)、当销售单价为58元时，每天销售量是件.

(2)、求销售该品牌童装获得的利润y（元）与销售单价x（元）之间的函数关系式；

(3)、若商场规定该品牌童装的销售单价不低于57元且不高于60元，则销售该品牌童装获得的最大利润是多少？

查看试题解析
27. 阅读理解：如图①，在四边形ABCD的边AB上任取一点E（点E不与A、B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的“相似点”；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题：

(1)、如图①，∠A＝∠B＝∠DEC＝45°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；

(2)、如图②，在矩形ABCD中，A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图②中画出矩形ABCD的边AB上的强相似点；

(3)、如图③，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB与BC的数量关系.

查看试题解析
28. 已知：平面直角坐标系内一直线：y＝﹣x+3分别与x轴、y轴交于B、C两点，抛物线y＝﹣x²+bx+c经过A、B两点，抛物线在x轴上方部分上有一动点D，连结AC；

(1)、求抛物线解析式；

(2)、当D在第一象限，求D到直线BC的最大距离；

(3)、是否存在D点某一位置，使∠DBC＝∠ACO？若存在，请直接写出D点坐标；若不存在，请说明理由.

查看试题解析

年龄/岁	12	13	14	15	16
人数	1	3	6	8	5