2021-2022学年浙教版七年级下册期中复习专题8 同底数幂除法及整式除法运算

试卷更新日期：2022-04-15 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列计算中，结果是 $x^{5}$ 的为（）

A、 $x^{2} \cdot x^{3}$ B、 $x^{6} - x$ C、 $x^{10} \div x^{2}$ D、 ${(x^{3})}^{2}$

查看试题解析
2. 下列各式添括号正确的是（）

A、 $- x + y = - (y - x)$ B、 $x - y = - (x + y)$ C、 $\begin{array}{l} 10 - m = 5 (2 - m) \end{array}$ D、 $\begin{array}{l} 3 - 2 a = - (2 a - 3) \end{array}$

查看试题解析
3. 若 $A$ 与 $- \frac{1}{2} a b$ 的积为 $- 4 a^{3} b^{3} + 3 a^{2} b^{2} - \frac{1}{2} a b$ ，则 $A$ 为（）

A、 $- 8 a^{2} b^{2} + 6 a b - 1$ B、 $- 2 a^{2} b^{2} + \frac{3}{2} a b + \frac{1}{4}$ C、 $8 a^{2} b^{2} - 6 a b + 1$ D、 $2 a^{2} b^{2} - \frac{3}{2} a b + 1$

查看试题解析
4. 若 $3 y - 2 x + 2 = 0$ ，则 $9^{x} \div 27^{y}$ 的值为（）

A、9 B、-9 C、 $\frac{1}{9}$ D、 $- \frac{1}{9}$

查看试题解析
5. 有下列计算：
① $(6 a b + 5 a) \div a = 6 b + 5$ ；② $(8 x^{2} y - 4 x y^{2}) \div (- 4 x y) = - 2 x - y$ ；③ $(15 x^{2} y z - 10 x y^{2}) \div (5 x y) = 3 x - 2 y$ ；④ $(5 m^{2} + 15 m^{3} n - 20 m^{4}) \div (- 5 m^{2}) = 4 m^{2} - 3 m n - 1$ ；⑤ $(3 x^{2} y - 3 x y^{2} + x) \div x = 3 x y - 3 y^{2}$ .

其中不正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在两个形状、大小完全相同的大长方形内，分别互不重叠地放入四个如图③的小长方形后得图①、图②，已知大长方形的长为2a，两个大长方形未被覆盖部分分别用阴影表示，则图①阴影部分周长与图②阴影部分周长的差是（）（用a的代数式表示）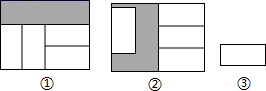

A、﹣a B、a C、﹣ $\frac{1}{2}$ a D、 $\frac{1}{2}$ a

查看试题解析
7. 在矩形ABCD内，将两张边长分别为a和b（ $a > b$ ）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $S_{1}$ ，图2中阴影部分的面积为 $S_{2}$ .当 $A D - A B = 3$ 时， $S_{2} - S_{1}$ 的值是（）

A、 $3 a$ B、 $3 b$ C、 $3 a - 3 b$ D、 $- 3 a$

查看试题解析
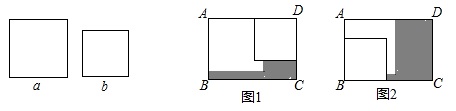8. 如图，长为50cm，宽为x(cm)的大长方形被分割成7小块，除阴影A，B外，其余5块是形状、大小完全相同的小长方形，其较短一边长为y(cm)．要使阴影A与阴影B的面积差不会随着x的变化而变化，则定值y为（）

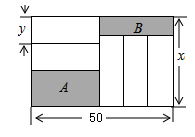A、5 B、 $\frac{25}{3}$ C、 $\frac{25}{2}$ D、10

查看试题解析
9. 小慧在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图1所示（其中 $b > a > c > 0$ ），售货员分别可按图2、图3、图4三种方法进行捆绑，设图2、图3、图4的捆绑绳长分别为 $l_{1} ， l_{2} ， l_{3}$ ，则 $l_{1} ， l_{2} ， l_{3}$ 的大小关系为（）

A、 $l_{1} > l_{3} > l_{2}$ B、 $l_{3} > l_{1} > l_{2}$ C、 $l_{1} > l_{2} > l_{3}$ D、 $l_{3} > l_{2} > l_{1}$

查看试题解析
10. 化简 $3 a b (a^{2} b - a b^{2} + a b) - a b^{2} (2 a^{2} - 3 a b + 2 a)$ 的结果是（）

A、 $a^{3} b^{2} + a^{2} b^{2}$ B、 $a^{2} b^{2} - a^{3} b^{2}$ C、 $a^{3} b^{2} - 6 a^{2} b^{3} + a^{2} b^{2}$ D、 $a^{3} b^{2} - a^{2} b^{2}$

查看试题解析

二、填空题

11. 若 $4^{x} = a ， 8^{y} = b$ ，则 $2^{2 x - 3 y}$ 可表示为（用含a、b的代数式表示）.

查看试题解析
12. 若 $2^{m} \times 8^{n} = 32$ ， $2^{m} \div 4^{n} = \frac{1}{16}$ ，则 $m + \frac{1}{2} n$ 的值为.

查看试题解析
13. 已知长方形的面积是 $49 a^{2} - 4 b^{2}$ ，一边长是 $7 a - 2 b$ ，则长方形的周长是.

查看试题解析
14. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
$\times (- \frac{1}{2} x y) = 3 x^{2} y - x y^{2} + \frac{1}{2} x y ，$

则当 $x = \frac{2}{3} ， y = \frac{1}{2}$ 时，所捂多项式的值是

查看试题解析
15. 如图，正方形ABCD、正方形CEFG的一边重合，它们边长分别为a ， b（a<b），则△BDF的面积是．

查看试题解析
16. 阅读材料：定义：如果一个数的平方等于﹣1，记为i²＝﹣1，这个数i叫做虚数单位，把形如a+bi（a，b为实数）的数叫做复数，其中a叫这个复数的实部，b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i；

（2﹣i）（3+i）＝6﹣3i+2i﹣i²＝6﹣i﹣（﹣1）＝7﹣i；

（4+i）（4﹣i）＝16﹣i²＝16﹣（﹣1）＝17；

（2+i）²＝4+4i+i²＝4+4i﹣1＝3+4i

根据以上信息，完成下面计算：

（1+2i）（2﹣i）+（2﹣i）²＝.

查看试题解析

三、计算题

17. 计算.

(1)、 $- 6 x^{2} y^{3} \div (2 x^{2} y)$ ；

(2)、 $(16 x^{2} y^{3} z + 8 x^{3} y^{2} z) \div (8 x y^{2})$ ；

查看试题解析
18. 先化简，后求值：

(1)、 $x (4 x + 2) - (2 x - 1) (2 x + 1)$ ，其中 $x = - 3$

(2)、 $\frac{a - 1}{a^{2} - 4} \div (1 - \frac{3}{a + 2})$ 先化简，再选择一个合适的数作为 $a$ 的值代入求值.

查看试题解析

四、解答题

19. 若 $5 x - 3 y + 2 = 0$ ，求 ${(10^{2 x})}^{3} \div (10^{x} \cdot 10^{3 y})$ 的值.

查看试题解析
20. 若|x﹣y+1|与（x+2y+4）²互为相反数，化简求代数[（2x+2y）²﹣（3x+y）（3x﹣y）﹣5y²]÷（2x）的值．

查看试题解析

五、综合题

21. 如图，某体育训练基地有一块长为(2a+b)米，宽为(a十b)米的长方形土地，现准备在这块长方形土地上修建一个长为a米，宽为(a-b)米的长方形游泳池(阴影部分)，剩余部分则全部修建成休息区域.(结果化简)

(1)、求长方形游泳池的面积；

(2)、求休息区域的面积.

查看试题解析
22. 点点与圆圆做游戏，两人各报一个整式，圆圆报的整式作为除式，点点报的整式作为被除式，要求商式必须是 $4 x^{2} y$ .

(1)、若点点报的是 $x^{7} y^{5} - 4 x^{5} y^{4} + 16 x^{2} y$ ，那么圆圆报的整式是什么?

(2)、若点点报的是 ${(- 2 x^{3} y^{2})}^{2} + 5 x^{3} y^{2}$ ，圆圆能报出一个整式吗?请说明理由.

查看试题解析
23. 如图，4张长为x，宽为y（x＞y）的长方形纸片拼成一个边长为（x＋y）的正方形ABCD.

(1)、用含x，y的代数式表示图中所有阴影部分面积的和；

(2)、当正方形ABCD的周长是正方形EFGH周长的三倍时，求 $\frac{x}{y}$ 的值；

(3)、在（2）的条件下，用题目条件中的4张长方形纸片，m张正方形ABCD纸片和n张正方形EFHG纸片（m，n为正整数），拼成一个大的正方形（拼接时无空隙、无重叠），当m，n为何值时，拼成的大正方形的边长最小？

查看试题解析