2021-2022学年浙教版初数八年级下学期期中模拟试卷(2)
试卷更新日期:2022-04-15 类型:期中考试
一、选择题
-
1. 下列计算错误的是( )A、 ﹣ = B、 ÷2= C、 D、3+2 =52. 如果一个多边形的每一个外角都是 ,则这个多边形的边数是( )A、6 B、8 C、10 D、123. 下列各式中,属于最简二次根式的是( )A、 B、 C、 D、4. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
5. 下列方程中,关于x的一元二次方程是( )A、2x-3=x B、2x+3y=5 C、2x-x2=1 D、x+ =76. 用配方法解方程x2-2x-2=0时,原方程应变形为( )A、(x+1)2=3 B、(x+2)2=6 C、(x-1)2=3 D、(x-2)2=67. 下列计算正确的是( )A、 - =3 B、 + =6 C、 × =2 D、 ÷ =48. 某商场销售额3月份为16万元,5月份为25万元,则这两个月销售额的月平均增长率为( )A、20% B、25% C、30% D、35%9. 如图,在Rt△ABC中,∠CBA=60°,斜边AB=10,分别以△ABC的三边长为边在AB上方作正方形,S1 , S2 , S3 , S4 , S5分别表示对应阴影部分的面积,则S1+S2+S3+S4+S5=( )
斐波那契螺旋线
5. 下列方程中,关于x的一元二次方程是( )A、2x-3=x B、2x+3y=5 C、2x-x2=1 D、x+ =76. 用配方法解方程x2-2x-2=0时,原方程应变形为( )A、(x+1)2=3 B、(x+2)2=6 C、(x-1)2=3 D、(x-2)2=67. 下列计算正确的是( )A、 - =3 B、 + =6 C、 × =2 D、 ÷ =48. 某商场销售额3月份为16万元,5月份为25万元,则这两个月销售额的月平均增长率为( )A、20% B、25% C、30% D、35%9. 如图,在Rt△ABC中,∠CBA=60°,斜边AB=10,分别以△ABC的三边长为边在AB上方作正方形,S1 , S2 , S3 , S4 , S5分别表示对应阴影部分的面积,则S1+S2+S3+S4+S5=( ) A、50 B、50 C、100 D、10010. 如表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:
A、50 B、50 C、100 D、10010. 如表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:甲
乙
丙
丁
平均数(环)
9.8
9.8
9.8
9.8
方差
0.85
0.72
0.88
0.76
根据表中数据,要从中选择一名成绩发挥稳定的运动员参加比赛,应选择( )
A、甲 B、乙 C、丙 D、丁二、填空题
-
11. 在函数 中,自变量x的取值范围是.12. 已知一个正多边形的一个内角是120度,则这个多边形的边数是.13. 某校男子足球队的年龄分布如图所示,则根据图中信息可知这些队员年龄的中位数是岁.
 14. 如图,在 中, , 为 的中线,过点 作 于点 ,过点 作 的平行线,交 的延长线于点 ,在 的延长线上截取 ,连接 , .若 , ,则四边形 的周长为.
14. 如图,在 中, , 为 的中线,过点 作 于点 ,过点 作 的平行线,交 的延长线于点 ,在 的延长线上截取 ,连接 , .若 , ,则四边形 的周长为. 15. 已知m是方程式x2+x﹣1=0的根,则式子m3+2m2+2019的值为.16. 已知一组数据x1 , x2 , x3 , x4 , x5的平均数是3,则数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数是 .
15. 已知m是方程式x2+x﹣1=0的根,则式子m3+2m2+2019的值为.16. 已知一组数据x1 , x2 , x3 , x4 , x5的平均数是3,则数据2x1﹣1,2x2﹣1,2x3﹣1,2x4﹣1,2x5﹣1的平均数是 .三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、x2-4×+1=0
(2)、(x-3)2+2x(x-3)=0
19. 如图,在方格纸中,线段AB的两个端点都在小方格的格点上,分别按下列要求画格点四边形.
(1)在图甲中画一个以AB为边的平行四边形﹔
(2)在图乙中画一个以AB为对角线的平行四边形.20. 疫情防控已成为常态化,为了解学生对疫情防控措施的知晓情况,某校保健室开展了“疫情防控知识”问卷测试(满分10分).他们将全校学生成绒进行统计,并随机抽取了40位同学的成绩绘制成如下的频数分布表和频数分布直方图(不完整).组号
成绩
频数
频率
1
2
0.050
2
6
0.150
3
a
0.450
4
9
0.225
5
b
m
6
2
0.050
合计
40
1.000

根据以上提供的信息,解答下列问题:
(1)、表格中 , , ;补全频数分布直方图;(2)、这40位同学成绩的中位数落在哪一个小组?(3)、全校共有1200位同学参与测试,若以组中值(每组成绩的中间数值)为本组数据的代表,请估计所有同学成绩的平均分大约是多少?21. 如图所示,在 中,AE,AF分别为BC,CD上的高,且 .求 各内角的度数.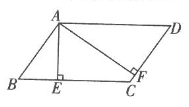 22. 如图,四边形 是平行四边形, 且分别交对角线 于点E , F .
22. 如图,四边形 是平行四边形, 且分别交对角线 于点E , F . (1)、求证: ;(2)、当四边形 分别是矩形和菱形时,请分别说出四边形 的形状.(无需说明理由)23. 已知:如图,在ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG= DH。
(1)、求证: ;(2)、当四边形 分别是矩形和菱形时,请分别说出四边形 的形状.(无需说明理由)23. 已知:如图,在ABCD中,对角线AC,BD相交于点O,点E,F在AC上,点G,H在BD上,且AE=CF,BG= DH。 (1)、若AC=6,BD=8,试求AD的取值范围;(2)、若AC=AD,∠CAD=50°,试求∠ABC的度数;(3)、求证:四边形EHFG是平行四边形。24. 如图,已知四边形ABCD是正方形,点E是AD边上的一点(不与点A,D重合),连接CE,以CE为一边作正方形CEFG,使点F,G与点A,B在CE的两侧,连接BE并延长,交GD延长线于点H.
(1)、若AC=6,BD=8,试求AD的取值范围;(2)、若AC=AD,∠CAD=50°,试求∠ABC的度数;(3)、求证:四边形EHFG是平行四边形。24. 如图,已知四边形ABCD是正方形,点E是AD边上的一点(不与点A,D重合),连接CE,以CE为一边作正方形CEFG,使点F,G与点A,B在CE的两侧,连接BE并延长,交GD延长线于点H.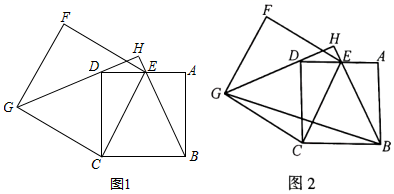 (1)、如图1,请判断线段BE与GD的数量关系和位置关系,并说明理由;(2)、如图2,连接BG,若AB=2,CE= , 请你直接写出的值.
(1)、如图1,请判断线段BE与GD的数量关系和位置关系,并说明理由;(2)、如图2,连接BG,若AB=2,CE= , 请你直接写出的值.