2022年苏科版初中数学《中考一轮复习》专题四 图形的认识 4.3 特殊三角形

试卷更新日期：2022-04-14 类型：二轮复习

进入 出卷网 下载

一、单选题

  • 1. 等腰三角形的顶角等于80°，则它的底角是（   ）
    A、80° B、50° C、40° D、80°或50°

    查看试题解析

  • 2. 下列各组数据作为三角形的三边长，能构成直角三角形的是（   ）
    A、 2 ， 3 ， 4 B、 5 ， 6 ， 30 C、 2 ， 5 ， 3 D、1.5，2，3

    查看试题解析

  • 3. 若直角三角形的两边长分别是5和12，则它的斜边长是（ ）
    A、13 B、13或 119 C、119 D、12或13

    查看试题解析

  • 4. 如图，B在AC上，D在CE上， AD=BD=BC ， ∠ACE=25° ， ∠ADE 的度数为（   ）

    A、50° B、65° C、75° D、80°

    查看试题解析

  • 5. 如图，AD是△ABC的角平分线，DE⊥AB于E ， 已知△ABC的面积为28.AC=6 ， DE=4 ， 则AB的长为（ ）

    A、4 B、6 C、8 D、10

    查看试题解析

  • 6. 如图，点P是∠AOB内任意一点，且∠AOB=40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为（   ）

    A、140 ° B、100° C、80° D、50°

    查看试题解析

  • 7. 如图，Rt△ABC中，AB=AC=3 ， AO=1 ， 若将AD绕A点逆时针旋转90°得到AE ， 连接OE ， 则在D点运动过程中，线段OE的最小值为（ ）

    A、1 B、2 C、3 D、2

    查看试题解析

  • 8. 如图，边长为5的等边三角形 A B C 中，M是高 C H 所在直线上的一个动点，连接 M B ，将线段 B M 绕点B逆时针旋转 60 ° 得到 B N ，连接 H N .则在点M运动过程中，线段 H N 长度的最小值是（   ）

    A、 5 4 B、1 C、2 D、 5 2

    查看试题解析

  • 9. 如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论中正确有（    ）

    ①△BPQ是等边三角形；②△PCQ是直角三角形；③∠APB＝150°；④∠APC＝120°．

     

    A、①②③ B、①②④ C、②③④ D、①②③④

    查看试题解析

  • 10. 如图所示，在平面直角坐标系中，点A1 ， A2 ， A3 ， …都在x轴上，点B1 ， B2 ， B3 ， …都在直线y=x上，△OA1B1 ， △B1A1A2 ， △B2B1A2 ， △B2A2A3 ， △B3B2A3 ， …都是等腰直角三角形，如果OA1=1 ， 则点B2021的坐标是（ ）

    A、(22021 ， 22021) B、(22020 ， 22020) C、(22019 ， 22019) D、(22018 ， 22018)

    查看试题解析

二、填空题

  • 11. 已知，等腰三角形的两边长分别为5cm和11cm，则它的周长是cm．

    查看试题解析

  • 12. 若等腰三角形的一个内角为 50° ，则这个等腰三角形的顶角为.

    查看试题解析

  • 13. 如图，在△ABC中，∠ACB=90° ， AD平分∠BAC交BC于点D，BC=10cm ， 点D到AB的距离为4cm ， 则BD的长为cm.

    查看试题解析

  • 14. 如图，在长方形ABCD中，AB=3 ， BC=4 ， 点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处.当△CEB'为直角三角形时，BE的长为.

    查看试题解析

  • 15. 如图，四边形ABCD中，∠ABC＝∠ADC＝90°，∠BCD＝135°，连接AC、BD.M是AC的中点，连接BM、DM.若AC＝10，则△BMD的面积为.

    查看试题解析

  • 16. 根据教材第65页“思考”栏目可以得到这样一个结论：如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，则AB＝2BC.请在这一结论的基础上继续思考：若AC＝2，点D是AB边上的动点，则CD+ 12 AD的最小值为.

    查看试题解析

  • 17. 如图，在边长为 23 的等边△ABC中，动点D，E分别在BC，AC边上，且保持AE＝CD，连接BE，AD，相交于点P，则CP的最小值为.

    查看试题解析

  • 18. 如图， ∠AOB 是一角度为 α 的锐角木架，要使木架更加牢固，需在其内部添加一些连接支撑木件 EF 、 FG 、 GH …，且 OE=EF=FG=GH …，在 OA 、 OB 足够长的情况下，如果最多能添加这样的连接支撑木件为6根，则锐角 α 的范围为.

    查看试题解析

三、解答题

  • 19. 如图所示的一块空地进行草坪绿化，已知 AD＝4m ，CD＝3m，AD⊥DC，AB＝13m ，BC＝12m ，绿化草坪价格 150 元/米2。求这块地草坪绿化的价钱．

     

    查看试题解析

  • 20. 已知：如图， ∠ABC=∠ADC=90∘ ，点 M 是 AC 的中点， MN⊥BD 于点 N ，求证： N 是 BD 的中点.

    查看试题解析

  • 21. 如图，长方形ABCD中，∠DAB=∠B=∠C=∠D=90°，AD=BC=16，AB=CD=34．点E为射线DC上的一个动点，△ADE与△AD′E关于直线AE对称，当△AD′B为直角三角形时，求DE的长.

    查看试题解析

  • 22. 如图， AD 是 ΔABC 的高线，且 BD=12AC ，E是 AC 的中点，连结 BE ，取 BE 的中点F，连结 DF ，求证： DF⊥BE .

    查看试题解析

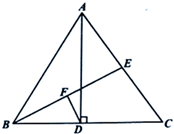  • 23. 如图①，在ΔABC中，∠ACB＝90°，D为AB中点，E为BC上一点，F为CA上一点，且FD⊥ED，垂足为D.

     

    (1)、若AF＝3.BE＝2，求FE的长；
    (2)、小明看到这个题目，提出这样的思路：如图②，延长ED到M，使得DM＝DE，连接AM，FM.首先证明∠FAM＝90°，再求出FM的长，最后得出FE的长，请你按照这个思路完成解答.
    若点E在边CB的延长线上，点F在边AC的延长线上，请直接写出AF、BE、FE的等量关系.

    查看试题解析

  • 24. 如图1，一次函数y＝ 4 3 x+4的图象与x轴、y轴分别交于点A、B.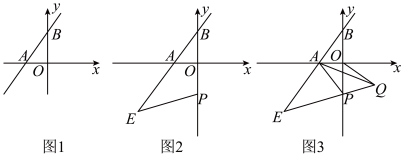

    (1)、则点A的坐标为 ， 点B的坐标为；
    (2)、如图2，点P为y轴上的动点，以点P为圆心，PB长为半径画弧，与BA的延长线交于点E，连接PE，已知PB＝PE，求证：∠BPE＝2∠OAB；
    (3)、在（2）的条件下，如图3，连接PA，以PA为腰作等腰三角形PAQ，其中PA＝PQ，∠APQ＝2∠OAB.连接OQ.

    ①则图中（不添加其他辅助线）与∠EPA相等的角有               ；（都写出来）

    ②试求线段OQ长的最小值.

    查看试题解析

  • 25. 问题情境：

    七下教材第149页提出这样一个问题：如图1，∠AOB＝90°，OC平分∠AOB，把三角尺的直角顶点落在OC的任意一点P上，并使三角尺的两条直角边分别与OA、OB相交于点E、F，PE与PF相等吗？

    (1)、七年级学习这部分内容时，我们还无法对这个问题的结论加以证明，八下教材第59页第11题不仅对这一问题给出了答案：“通过实验可以得到PE＝PF”，还要求“现在请你证明这个结论”，请你给出证明：
    (2)、变式拓展：
    如图2，已知∠AOB＝120°，OC平分∠AOB，P是OC上一点，∠EPF＝60°，PE边与OA边相交于点E，PF边与射线OB的反向延长线相交于点F.试解决下列问题：

    ①PE与PF还相等吗？为什么？

    ②试判断OE、OF、OP三条线段之间的数量关系，并说明理由.

    查看试题解析

  • 26. 如图，在平面直角坐标系中O为坐标原点，点A（6，0），点B（0，8）点C（－2，0），点P从B出发沿BA向A运动，速度为每秒1单位长度，点P运动的同时，点Q从A出发沿AC向C运动，速度为每秒2个单位长度，当点Q到达点C时，P，Q同时停止运动，设P，Q两点运动时间为t秒.

    (1)、当t为何值时，PQ//BC；
    (2)、若点E是点B以P为对称中心的对称点，

    ①当ΔPEQ的面积是ΔABC面积的 25 时，求出此时t的值：

    ②当t为何值时，以A、E、Q其中一点为圆心的圆恰好过另外两个点.（直接写出结果）

    查看试题解析