北师大版备考2022中考数学二轮复习专题12 二次函数的图象与性质
试卷更新日期:2022-04-14 类型:二轮复习
一、单选题
-
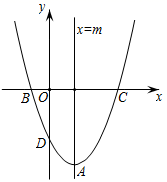
1. 二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与一次函数y=bx+c在同一坐标系内的大致图象是( )
 A、
A、 B、
B、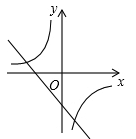 C、
C、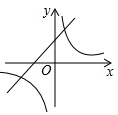 D、
D、 2. 将抛物线在x轴上方的部分记为 , 在x轴上及其下方的部分记为 , 将沿x轴向下翻折得到 , 和两部分组成的图象记为M.若直线与M恰有2个交点,则m的取值范围为( )A、或 B、或 C、 D、或3. 求二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 、 ,其中 ,有下列结论:① ;② ;③ ;④ ;⑤ ;其中,正确的结论有( )
2. 将抛物线在x轴上方的部分记为 , 在x轴上及其下方的部分记为 , 将沿x轴向下翻折得到 , 和两部分组成的图象记为M.若直线与M恰有2个交点,则m的取值范围为( )A、或 B、或 C、 D、或3. 求二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 、 ,其中 ,有下列结论:① ;② ;③ ;④ ;⑤ ;其中,正确的结论有( ) A、5 B、4 C、3 D、24. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A、5 B、4 C、3 D、24. 将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )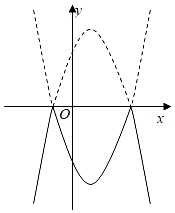 A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣35. 如图,抛物线 (a>0)与x轴交于A,B,顶点为点D,把抛物线在x轴下方部分关于点B作中心对称,顶点对应D′,点A对应点C,连接DD′,CD′,DC,当△CDD′是直角三角形时,a的值为( )
A、 或﹣3 B、 或﹣3 C、 或﹣3 D、 或﹣35. 如图,抛物线 (a>0)与x轴交于A,B,顶点为点D,把抛物线在x轴下方部分关于点B作中心对称,顶点对应D′,点A对应点C,连接DD′,CD′,DC,当△CDD′是直角三角形时,a的值为( ) A、 或 B、 或 C、 或 D、 或6. 抛物线 (a,b,c为常数)开口向下且过点 , ( ),下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是( )A、4 B、3 C、2 D、17. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、48. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形 中,点 ,点 ,则互异二次函数 与正方形 有交点时 的最大值和最小值分别是( )
A、 或 B、 或 C、 或 D、 或6. 抛物线 (a,b,c为常数)开口向下且过点 , ( ),下列结论:① ;② ;③ ;④若方程 有两个不相等的实数根,则 .其中正确结论的个数是( )A、4 B、3 C、2 D、17. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、48. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形 中,点 ,点 ,则互异二次函数 与正方形 有交点时 的最大值和最小值分别是( ) A、4,-1 B、 ,-1 C、4,0 D、 ,-19. 如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
A、4,-1 B、 ,-1 C、4,0 D、 ,-19. 如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
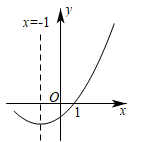
① ;
② ;
③关于x的一元二次方程 的两根分别为-3和1;
④若点 , , 均在二次函数图象上,则 ;
⑤ (m为任意实数).
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个10. 已知二次函数y=-x2+x+6及一次函数y=-x+m,将该二次函数在x轴上方的图像沿x轴翻折到x轴的下方,图像的其余部分不变,得到一个新图像(如图所示).当直线y=-x+m与新图像有4个交点时,m的取值范围是( ) A、 B、 C、 D、11. 如图,在平面直角坐标系 中,函数 的图像与对称轴直线 交于点A,与 轴交于 三点,下列命题正确的是( )
A、 B、 C、 D、11. 如图,在平面直角坐标系 中,函数 的图像与对称轴直线 交于点A,与 轴交于 三点,下列命题正确的是( )① ;②若 ,则 ;③对于任意 ,始终有 ;④若B的坐标为 ,则C的坐标为 .
 A、①②③ B、①②④ C、①③④ D、②③④12. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )
A、①②③ B、①②④ C、①③④ D、②③④12. 如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )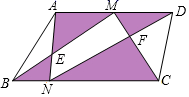 A、不变 B、一直变大 C、先减小后增大 D、先增大后减小
A、不变 B、一直变大 C、先减小后增大 D、先增大后减小二、填空题
-
13. 二次函数 与两坐标轴的三个交点确定的三角形的面积是 .14. 将抛物线 向右平移 个单位,再向下平移 个单位后所得到新抛物线的解析式是 , 顶点坐标是 .15. 已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论:
①b<1;②c<2;③0<m< ;④n≤1.
则所有正确结论的序号是 .
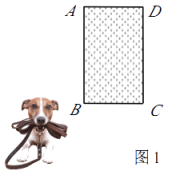
16.在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.
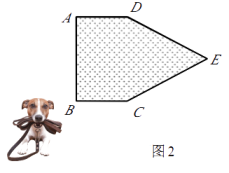 17. 已知正方形ABCD中A(1,1)、B(1,2)、C(2,2)、D(2,1),有一抛物线y=(x+1)2向下平移m个单位(m>0)与正方形ABCD的边(包括四个顶点)有交点,则m的取值范围是 .18. 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC外作等边三角形BDE。若F为DE的中点,则CF的最小值为 。
17. 已知正方形ABCD中A(1,1)、B(1,2)、C(2,2)、D(2,1),有一抛物线y=(x+1)2向下平移m个单位(m>0)与正方形ABCD的边(包括四个顶点)有交点,则m的取值范围是 .18. 如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=4,D为线段AB上一个动点,以BD为边在△ABC外作等边三角形BDE。若F为DE的中点,则CF的最小值为 。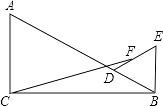 19. 已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ,则a的值为 .20. 如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .
19. 已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ,则a的值为 .20. 如图,把抛物线y= x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= x2交于点Q,则图中阴影部分的面积为 .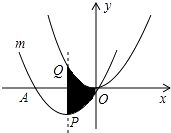
三、作图题
-
21. 已知二次函数y=﹣x2+2x+3图象的对称轴为直线.
 (1)、请求出该函数图象的对称轴;(2)、在坐标系内作出该函数的图象;(3)、有一条直线过点P(1,5),若该直线与二次函数y=﹣x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.
(1)、请求出该函数图象的对称轴;(2)、在坐标系内作出该函数的图象;(3)、有一条直线过点P(1,5),若该直线与二次函数y=﹣x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.四、解答题
-
22. 交通工程学理论把在单向道路上行驶的汽车看成连续的液体,并用流量、速度、密度三个概念描述车流的基本特征。其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度(辆/千米)指通过道路指定断面单位长度内的车辆数,为配合大数据治堵行动,测得某路段流量q与速度v之间的部分数据如下表:
速度v(千米/小时)
…
5
10
20
32
40
48
…
流量q(辆/小时)
…
550
1000
1600
1792
1600
1152
…
(1)、根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是(只需填上正确答案的序号)① ② ③(2)、请利用(1)中选取的函数关系式分析,当该路段的车流速为多少时,流量达到最大?最大流量是多少?(3)、已知q,v,k满足 ,请结合(1)中选取的函数关系式继续解决下列问题:①市交通运行监控平台显示,当 时道路出现轻度拥堵,试分析当车流密度k在什么范围时,该路段出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值
23. 如图,已知抛物线y=﹣x2﹣2x+m+1与x轴交于A(x1 , 0)、B(x2 , 0)两点,且x1<0,x2>0,与y轴交于点C,顶点为P.(提示:若x1 , x2是一元二次方程ax2+bx+c=0(a≠0)的两个实根,则x1+x2=﹣ ,x1•x2= ) (1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(1)、求m的取值范围;(2)、若OA=3OB,求抛物线的解析式;
(3)、在(2)中抛物线的对称轴PD上,存在点Q使得△BQC的周长最短,试求出点Q的坐标.五、综合题
-
24.
如图,抛物线 经过点 ,交y 轴于点C:
 (1)、求抛物线的解析式(用一般式表示).(2)、点 为 轴右侧抛物线上一点,是否存在点 使 ,若存在请直接给出点 坐标;若不存在请说明理由.(3)、将直线 绕点 顺时针旋转 ,与抛物线交于另一点 ,求 的长.25. 如图,在平面直角坐标系中,已知点B的坐标为(﹣1,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.
(1)、求抛物线的解析式(用一般式表示).(2)、点 为 轴右侧抛物线上一点,是否存在点 使 ,若存在请直接给出点 坐标;若不存在请说明理由.(3)、将直线 绕点 顺时针旋转 ,与抛物线交于另一点 ,求 的长.25. 如图,在平面直角坐标系中,已知点B的坐标为(﹣1,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.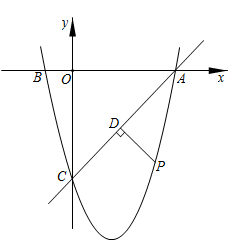 (1)、求A,C两点的坐标;(2)、求抛物线的解析式;(3)、若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.26.
(1)、求A,C两点的坐标;(2)、求抛物线的解析式;(3)、若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.26.如图,直线y=﹣ x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣ x2+bx+c经过点A,B.
 (1)、求点B的坐标和抛物线的解析式;(2)、M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)、求点B的坐标和抛物线的解析式;(2)、M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;
②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.
-