2021-2022学年浙教版七年级下册期中复习专题6 同底数幂乘法及多项式乘法运算

试卷更新日期：2022-04-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列运算中，正确的是（）

A、（﹣a）⁶÷（﹣a）³＝﹣a³ B、（﹣3a³）²＝6a⁶ C、（ab²）³＝ab⁶ D、a³•a²＝a⁶

查看试题解析
2. 计算 $2^{101} \times {0.5}^{100}$ 的结果是（）

A、1 B、2 C、0.5 D、10

查看试题解析
3. （） $\times a b = 2 a b^{2}$ ，则括号内应填的单项式是（）

A、2 B、2a C、2b D、4b

查看试题解析
4. 小明总结了以下结论：
① $a (b + c) = a b + a c$ ；② $a (b - c) = a b - a c$ ；③ $(b - c) \div a = b \div a - c \div a (a \neq 0)$ ；④ $a \div (b + c) = a \div b + a \div c (a \neq 0)$ .

其中一定成立的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 某天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：- $3 x y (4 y - 2 x -$ $1) = - 12 x y^{2} + 6 x^{2} y + □ ， □$ 的地方被钢笔水弄污了，你认为 $□$ 内应填写（）

A、3xy B、 $- 3 x y$ C、-1 D、1

查看试题解析
6. 若 $(x + 2) (x - 1) = x^{2} + m x + n$ ，则 $m + n =$ （）

A、1 B、-2 C、-1 D、2

查看试题解析
7. 已知 $(x - 5) (x + ☆) = x^{2} - 2 x - 15$ ，其中☆代表一个常数，则☆的值为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如果计算（ $x + m$ ）（ $x + \frac{1}{3}$ ）的结果中不含关于 $x$ 的一次项，那么 $m$ 的值为（）

A、- $\frac{1}{3}$ B、 $\frac{1}{3}$ C、-3 D、3

查看试题解析
9. 若 $A \cdot (m^{2} - 3 n) = m^{3} - 3 m n$ ，则代数式 $A$ 为（）

A、 $m$ B、mn C、 $m n^{2}$ D、 $m^{2} n$

查看试题解析
10. 如图是一栋楼房的平面图，下列式子中不能表示它的面积的是（）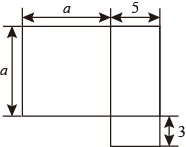

A、 $a^{2} + 5 a + 15$ B、（a＋5）（a＋3）－3a C、a（a＋5）＋15 D、 $a (a + 3) + a^{2}$

查看试题解析

二、填空题

11. 若 $2^{m} = a ， 4^{n} = b$ ，m、n为正整数，则 $2^{3 m + 4 n} =$ ．（用含a、b的代数式表示）

查看试题解析
12. 已知2^a= $\frac{1}{3}$ ，8^b=12，则（a+3b-4）²的值是.

查看试题解析
13. 已知 $3^{a} = 4$ ， $3^{b} = 10$ ， $3^{c} = 25$ ，则 $a$ ， $b$ ， $c$ 之间满足的等量关系是.

查看试题解析
14. 我们知道，同底数幂的乘法法则为a^m·aⁿ=a^m+n（其中a≠0，m、n为正整数），类似地我们规定关于任意正整数m、n的一种新运算：h（m+n）=h（m） ·h（n）；比如h（2）=5，则h（4）=h（2+2）=5×5=25．若h（3）=k（k≠0）。则h（3b）·h（27）（其中b为正整数）的结果是。

查看试题解析
15. 若3x²+kx+4被3x﹣1除后余2，则k的值为．

查看试题解析
16. 观察下列各数，按照某种规律在横线上填上一个适当的数。
$- \frac{1}{4}$ ， $\frac{2}{8}$ ， $- \frac{3}{16}$ ， $\frac{4}{32}$ ， $- \frac{5}{64}$ ，.

查看试题解析

三、计算题

17. 用简便运算进行计算：

(1)、 $(\frac{1}{2} - \frac{1}{6} + \frac{1}{3}) \times (- 24) ；$

(2)、 ${(- 0.25)}^{2019} \times 4^{2020} ；$

查看试题解析
18. 计算或化简

(1)、（14a³﹣7a²）÷（7a）；

(2)、（a+b）（a²﹣ab+b²）.

查看试题解析

四、综合题

19. 若 $a^{m} = a^{n} (a > 0$ 且 $a \neq 1 ， m ， n$ 是正整数)，则 $m = n$ .利用上面的结论解决下面的问题.

(1)、如果 $2 \div 8^{x} \cdot 16^{x} = 2^{5}$ ，求 $x$ 的值；

(2)、如果 $2^{x + 2} + 2^{x + 1} = 24$ ，求 $x$ 的值.

查看试题解析
20. 阅读材料，解答问题：
在(x²+ax+b)(2x²-3x-1)的结果中，x³项的系数为-5，x²项的系数为-6，求a，b的值。

解：原式=2x⁴-3x³-x²+2ax³-3ax²-ax+2bx²-3bx-b①，

=2x⁴-(3+2a)x³-(1-3a+2b)x²-(a-3b)x-b②，

由题可知 ${\begin{cases} 3 + 2 a = 5 \\ 1 - 3 a + 2 b = 6 \end{cases}$ ，解得 ${\begin{cases} a = 1 \\ b = 4 \end{cases}$ ③

(1)、上述解答过程是否正确？若不正确，从第步开始出现错误。

(2)、请你写出正确的解答过程。

查看试题解析
21.

(1)、若x^m＝2，xⁿ＝3．求x^m+2n的值；

(2)、先化简，再求值：[（x﹣3y）²﹣x（2x﹣4y）+x²]÷（﹣2y），其中x＝1，y＝2．

查看试题解析
22.

(1)、若 $2 x + 3 y - 4 z + 1 = 0$ ，求 $9^{x} \cdot 27^{y} \div$ $81^{2}$ 的值.

(2)、若 $(x^{2} + n x + 3) (x^{2} - 3 x + m)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 的项，求m，n的值.

查看试题解析
23. 计算下列各式.

(1)、 $(x - 1) (x + 1) =$ .

$(x - 1) (x^{2} + x + 1) =$ .

$(x - 1) (x^{3} + x^{2} + x + 1) =$ .

……

(2)、根据以上规律，直接写出下式的结果：
$(x - 1) (x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1) =$

(3)、你能否由此归纳出一般性的结论：
$(x - 1) (x^{n - 1} + x^{n - 2} + x^{n - 3} + \dots + x + 1) =$ （其中 $n$ 为正整数）；

(4)、根据(2)的结论写出 $1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots +$ $2^{35}$ 的结果.

查看试题解析