北师大版备考2022中考数学二轮复习专题11 反比例函数
试卷更新日期:2022-04-14 类型:二轮复习
一、单选题
-
1. 如图,直线 与 轴、 轴分别相交于点A、B,过点B作 ,使 .将 绕点 顺时针旋转,每次旋转 .则第2022次旋转结束时,点 的对应点 落在反比例函数 的图象上,则 的值为
 A、-4 B、4 C、-6 D、62. 已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( )
A、-4 B、4 C、-6 D、62. 已知反比例函数y=(k≠0)的图象如图所示,则一次函数y=kx+2的图象经过( ) A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限3. 如图所示的是反比例函数和一次函数的图象,则下列结论正确的是( )
A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限3. 如图所示的是反比例函数和一次函数的图象,则下列结论正确的是( ) A、反比例函数的解析式是 B、一次函数的解析式为 C、当时, D、若 , 则4. 反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )A、
A、反比例函数的解析式是 B、一次函数的解析式为 C、当时, D、若 , 则4. 反比例函数y=﹣与一次函数y=x﹣2在同一坐标系中的大致图象可能是( )A、 B、
B、 C、
C、 D、
D、 5. 如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( )
5. 如图, 中, , ,点 在反比例函数 的图象上, 交反比例函数 的图象于点 ,且 ,则 的值为( ) A、-2 B、-4 C、-6 D、-86. 如图, 的边 在x轴上,边 交y轴于点E, ,反比例函数 过C点,且交线段 于D, ,连接 ,若 ,则k的值为( )
A、-2 B、-4 C、-6 D、-86. 如图, 的边 在x轴上,边 交y轴于点E, ,反比例函数 过C点,且交线段 于D, ,连接 ,若 ,则k的值为( ) A、 B、 C、4 D、67. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、88. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )
A、 B、 C、4 D、67. 平面直角坐标系 中,直线 与双曲线 相交于A,B两点,其中点A在第一象限.设 为双曲线 上一点,直线 , 分别交y轴于C,D两点,则 的值为( )A、2 B、4 C、6 D、88. 如图,点P是函数 的图像上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数 的图像于点C、D,连接 、 、 、 ,其中 ,下列结论:① ;② ;③ ,其中正确的是( )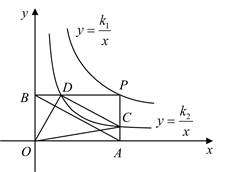 A、①② B、①③ C、②③ D、①9. 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n , 2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m , 则k的值是( )
A、①② B、①③ C、②③ D、①9. 如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数 (k<0)的图象在第二象限交于A(﹣3,m),B(n , 2)两点.若点E在x轴上,满足∠AEB=90°,且AE=2﹣m , 则k的值是( ) A、 B、 C、 D、10. 如图,四边形OABC是平行四边形,点A的坐标为A(3,0),∠COA = 60°,D为边AB的中点,反比例函数y = (x > 0)的图象经过C,D两点,直线CD与y轴相交于点E,则点E的坐标为( )
A、 B、 C、 D、10. 如图,四边形OABC是平行四边形,点A的坐标为A(3,0),∠COA = 60°,D为边AB的中点,反比例函数y = (x > 0)的图象经过C,D两点,直线CD与y轴相交于点E,则点E的坐标为( ) A、(0,2 ) B、(0,3 ) C、(0,5) D、(0,6)11. 如图,在平面直角坐标系中,菱形 的顶点A,D在反比例函数 的图象上,对角线 平行x轴,点O在 上,且 ,连接 , ,若 ,则k的值为( )
A、(0,2 ) B、(0,3 ) C、(0,5) D、(0,6)11. 如图,在平面直角坐标系中,菱形 的顶点A,D在反比例函数 的图象上,对角线 平行x轴,点O在 上,且 ,连接 , ,若 ,则k的值为( ) A、25 B、 C、45 D、12. 如图,已知 的一边 平行于 轴,且反比例函数 经过 顶点 和 上的一点 ,若 且 的面积为 ,则 的值为( )
A、25 B、 C、45 D、12. 如图,已知 的一边 平行于 轴,且反比例函数 经过 顶点 和 上的一点 ,若 且 的面积为 ,则 的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
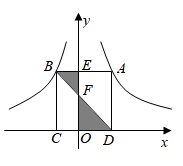 14. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 .
14. 如图,点、都在反比例函数的图象上,点是直线上的一个动点,则的最小值是 . 15. 已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .16. 在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y= (m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P , 使得S△ABP=2S△ABO , 那么点P的坐标是 .17. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.
15. 已知,一次函数与反比例函数的图象交于点A、B,在x轴上存在点P(n,0),使△ABP为直角三角形,则P点的坐标是 .16. 在平面直角坐标系中,点A(﹣4,1)为直线y=kx(k≠0)和双曲线y= (m≠0)的一个交点,点B(﹣5,0),如果在直线y=kx上有一点P , 使得S△ABP=2S△ABO , 那么点P的坐标是 .17. 如图,在平面直角坐标系中, 斜边上的高为1, ,将 绕原点顺时针旋转 得到 ,点A的对应点C恰好在函数 的图象上,若在 的图象上另有一点M使得 ,则点M的坐标为.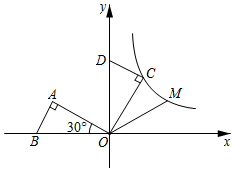 18. 如图,双曲线y= (x<0)经过平行四边形OABC的顶点C , 交边AB于点N , 交对角线AC于点M , 延长AC交y轴于点D , 连接OM . 若BN:AN=2:1,且S△OCM的面积为4,则k的值为 .
18. 如图,双曲线y= (x<0)经过平行四边形OABC的顶点C , 交边AB于点N , 交对角线AC于点M , 延长AC交y轴于点D , 连接OM . 若BN:AN=2:1,且S△OCM的面积为4,则k的值为 . 19. 如图,在平面直角坐标系中,双曲线 ( )与直线 ( )交于A、B两点,点H是双曲线第一象限上的动点(在点A左侧),直线AH、BH分别与y轴交于P、Q两点,若 , ,则a-b的值为.
19. 如图,在平面直角坐标系中,双曲线 ( )与直线 ( )交于A、B两点,点H是双曲线第一象限上的动点(在点A左侧),直线AH、BH分别与y轴交于P、Q两点,若 , ,则a-b的值为. 20. 如图, 的顶点 在反比例函数 的图象上,顶点 在 轴的正半轴上,顶点 和 在反比例函数 的图象上,且对角线 轴,则 的面积等于 .
20. 如图, 的顶点 在反比例函数 的图象上,顶点 在 轴的正半轴上,顶点 和 在反比例函数 的图象上,且对角线 轴,则 的面积等于 . 21. 如图,经过原点的直线与反比例函数y= (k>0)相交于A,B两点,BC⊥x轴。若△ABC的面积为4,则k的值为。
21. 如图,经过原点的直线与反比例函数y= (k>0)相交于A,B两点,BC⊥x轴。若△ABC的面积为4,则k的值为。 22. 如图,经过原点O的直线与反比例函数 (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数 (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则 的值为 , 的值为.
22. 如图,经过原点O的直线与反比例函数 (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数 (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则 的值为 , 的值为.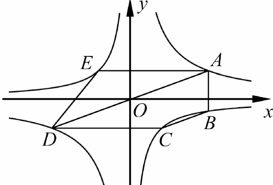
三、作图题
-
23. 启航同学根据学习函数的经验,对函数 的图象与性质进行了探究.下面是他的探究过程,请补充完成:
 (1)、函数 的自变量x 的取值范围是;(2)、列表,找出y 与x 的几组对应值,列表如下:
(1)、函数 的自变量x 的取值范围是;(2)、列表,找出y 与x 的几组对应值,列表如下:x
…
-2
-1
0
2
3
..
y
…
a
1
2
2
1
…
其中, a=;
(3)、在平面直角坐标系xOy 中,描出以上表中各对对 应值为坐标的点,并画出该函数的图象并写出该函数的一条性质:四、解答题
-
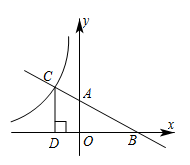
24. 如图所示,直线 交坐标轴于A , B两点,与反比例函数 交于点C , 过点C作x轴的垂线,垂足为D . 若 ,求k的值.
 25. 如图,D为反比例函数 的图象上一点,过D作DE⊥ 轴于点E,DC⊥ 轴于点C,一次函数 的图象经过C点,与 轴相交于A点,四边形DCAE的面积为4,求 的值.
25. 如图,D为反比例函数 的图象上一点,过D作DE⊥ 轴于点E,DC⊥ 轴于点C,一次函数 的图象经过C点,与 轴相交于A点,四边形DCAE的面积为4,求 的值.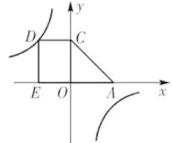
五、综合题
-
26. 如图,矩形的顶点A,C分别落在x轴,y轴的正半轴上,顶点 , 反比例函数的图象与 , 分别交于D,E, .
 (1)、求反比例函数关系式和点E的坐标;(2)、写出与的位置关系并说明理由;(3)、点F在直线上,点G是坐标系内点,当四边形为菱形时,求出点G的坐标.27. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
(1)、求反比例函数关系式和点E的坐标;(2)、写出与的位置关系并说明理由;(3)、点F在直线上,点G是坐标系内点,当四边形为菱形时,求出点G的坐标.27. 如图,在平面直角坐标系中,A (6,0)、B(0, 4)是矩形OACB的两个顶点,双曲线 (k≠0,x>0)经过AC的中点D,点E是矩形OACB与双曲线 的另一个交点,
 (1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .
(1)、点D的坐标为 , 点E的坐标为.(2)、动点P在第一象限内,且满足 .①若点P在这个反比例函数的图象上,求点P的坐标;
②连接PO、PE,当PO-PE的值最大时,求点P的坐标;
③若点Q是平面内一点,使得以A、C、P、Q为顶点的四边形是菱形,请你直接写出满足条件的所有点Q的坐标.
28. 数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题.猜想发现:由 ; ; ; ; ;
猜想:如果 , ,那么存在 (当且仅当 时等号成立).
猜想证明:∵
∴①当且仅当 ,即 时, ,∴ ;
②当 ,即 时, ,∴ .
综合上述可得:若 , ,则 成立(当日仅当 时等号成立).
(1)、猜想运用:对于函数 ,当x取何值时,函数y的值最小?最小值是多少?(2)、变式探究:对于函数 ,当x取何值时,函数y的值最小?最小值是多少?(3)、拓展应用:(3)疫情期间、为了解决疑似人员的临隔离问题.高速公路榆测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图.设每间离房的面积为S(米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S最大?最大面积是多少?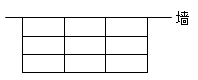
-