2022年江苏省徐州市中考数学模拟卷1

试卷更新日期：2022-04-14 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共24分）

1. 比-2小的数是（）

A、2 B、0 C、 $- 2^{2}$ D、 $- (- 1)$

查看试题解析
2. 第24届冬季奥林匹克运动会于2月4日﹣20日在北京和河北张家口举行.下列体育运动项目图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、 $2 a^{3} \cdot a^{4} = a^{12}$ B、 $2 \sqrt{2} \times \sqrt{2} = 4$ C、 ${(2 a^{4})}^{3} = 8 a^{7}$ D、 $a^{8} \div a^{2} = a^{4}$

查看试题解析
4. 如图，有4张形状大小质地均相同的卡片，正面印有速度滑雪．雪橇、冰壶、冬季两项等四种不同的图案，背面完全相同：

现将这4张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面恰好是冰壶项目图案的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
5. 在某校选拔毕业晚会主持人的决赛中，参与投票的每名学生必须从进入决赛的四名选手中选1名，且只能选1名，根据投票结果，绘制了如下两幅不完整的统计图，则选手B的得票为（）

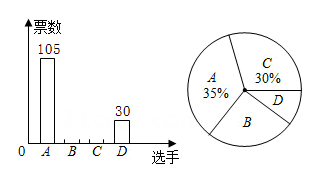A、300 B、90 C、75 D、85

查看试题解析
6. 估计 $(\sqrt{24} + \sqrt{6}) \div \sqrt{2}$ 的值应在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
7. 将抛物线 $y = x^{2} - 2 x - 1$ 向上平移1个单位，平移后所得抛物线的表达式是（）

A、 $y = x^{2} - 2 x$ B、 $y = x^{2} - 2 x - 2$ C、 $y = x^{2} - x - 1$ D、 $y = x^{2} - 3 x - 1$ .

查看试题解析
8. 如图，在Rt△ABC中，∠B＝90°，AB＝8，BC＝6，延长BC至E，使得CE＝BC，将△ABC沿AC翻折，使点B落点D处，连接DE，则DE的长为（）

A、 $\frac{18}{5}$ B、 $\frac{24}{5}$ C、 $\frac{32}{5}$ D、 $\frac{36}{5}$

查看试题解析

二、填空题（每题3分，共30分）

9. 按照“双减”要求，寒假减少作业量，同学们的假期拥有更多自由时间，据禹鑫小朋友统计，2021年寒假他练习书法一共书写40500个字，将40500用科学记数法表示为．

查看试题解析
10. 已知：x-2的平方根是±2， $2 x + y + 7$ 的立方根为3，则 $x^{2} + y^{2}$ 的算术平方根为.

查看试题解析
11. 分解因式：m²+1﹣2m＝.

查看试题解析
12. 使 $\frac{1}{\sqrt{x - 3}}$ 有意义的x的取值范围是.

查看试题解析
13. 若关于x的一元二次方程 $x^{2} - b x + 2 = 0$ 有一个根为1，则方程另一个根为.

查看试题解析
14. 如图，点A、B、C在⊙O上，∠ACB+∠AOB=90°，则∠ACB的大小为

查看试题解析
15. 已知圆锥的底面半径为5cm，母线长为13cm，则这个圆锥的侧面积是.

查看试题解析
16. 如图， $R t △ A B C$ 中， $∠ C = 9 0^{∘}$ ，点 $D$ 、 $E$ 、 $F$ 分别在 $B C$ 、 $A B$ 、 $A C$ 上，且四边 $C D E F$ 是正方形.若 $A E = 4$ ， $B E = 3$ ， $S_{R t △ A F E} = S_{1}$ ， $S_{R t △ B D E} = S_{2}$ ，则 $S_{1} + S_{2} =$ .

查看试题解析
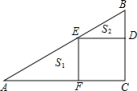17. 如图，矩形ABCD的顶点A、B分别在反比例函数 $y = \frac{12}{x} (x > 0)$ 与 $y = - \frac{6}{x} (x < 0)$ 的图象上，点C、D在x轴上，AB、BD分别交y轴于点E、F，则阴影部分的面积为．

查看试题解析
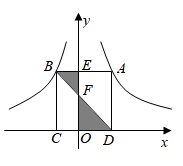18. 如图，在矩形ABCD中，AB＝8，AD＝10，AD，AB，BC分别与⊙O相切于E，F，G三点，过D作⊙O的切线交BC于点M，切点为N，则DM的长为 .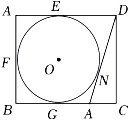

查看试题解析

三、解答题（共10题，共86分）

19. 计算：

(1)、 ${(m - n)}^{2} - m (m - 2 n)$

(2)、 $\frac{x^{2} - 2 x}{x^{2} - 1} \div (1 - \frac{2 x - 1}{x + 1})$

查看试题解析
20.

(1)、计算： $\sin 60 ° - \sqrt{12} \times \sqrt{3} - {(π - 3.14)}^{0} + 2^{- 2}$

(2)、解不等式组 ${\begin{matrix} 2 x + 7 \geq 1 - x ， ① \\ 6 - 3 (1 - x) > 5 x ， ② \end{matrix}$

查看试题解析
21. 如图，四边形 $A B C D$ 是平行四边形.

(1)、尺规作图（不写作法，保留作图痕迹）；作出 $∠ A B C$ 的角平分线 $B E$ ，交 $A D$ 于点 $E$ ；在线段 $B C$ 上截取 $B F = B A$ ，连接 $E F$ ；

(2)、在（1）所作图中，请判断四边形 $A B F E$ 的形状，并说明理由.

查看试题解析
22. 如图，AB为⊙O的直径，BC是⊙O的一条弦，点D在⊙O上，BD平分∠ABC，过点D作EF⊥BC，分别交BA、BC的延长线于点E、F.

(1)、求证：EF为⊙O的切线；

(2)、若BD＝4 $\sqrt{5}$ ，tan∠FDB＝2，求AE的长.

查看试题解析
23. A、B两地相距480km，甲、乙两人同时从A地匀速驶往B地，已知甲的行驶速度是乙的行驶速度的1.2倍，甲比乙提前1h到达B地，求甲、乙两人的行驶速度各是多少？

查看试题解析
24. 据《重庆晨报》，2007年，重庆市被国家评为无偿献血先进城市，医疗临床用血实现了100%来自市民自愿献血，无偿献血总量6.5吨，居全国第三位．现有小莉，小罗，小强三个自愿献血者，两人血型为O型，一人血型为A型．若在三人中随意挑选一人献血，两年以后又从此三人中随意挑选一人献血，试求两次所抽血的血型均为O型的概率．（要求：用列表或画树状图的方法解答）

查看试题解析
25. 某学校为了了解本校1200名学生的课外阅读的情况，现从各年级随机抽取了部分学生对他们一周的课外阅读时间进行了调查，并绘制出如下的统计图①和图②，根据相关信息，解答下列问题：

(1)、本次接受随机抽样调查的学生人数为图①中m的值为；

(2)、本次调查获取的样本数据的众数为，中位数为；

(3)、求本次调查获取的样本数据平均数；

(4)、根据样本数据，估计该校一周的课外阅读时间大于6h的学生人数.

查看试题解析
26. 如图，已知直线y＝ $- \frac{3}{4}$ x+3与x轴交于点B，与y轴交于点C，抛物线y＝ax²+bx+3经过B、C两点并与x轴的另一个交点为A，且OC＝3OA.

(1)、求抛物线的解析式；

(2)、点D为直线BC上方对称轴右侧抛物线上一点，当△DBC的面积为 $\frac{9}{2}$ 时，求D点的坐标；

(3)、在（2）的条件下，连接CD，作DE⊥x轴于E，BC、DE交于点H，点P为线段CD上一个动点，过点P作PF∥AC交x轴于点F，连接FH，当∠PFH＝45°时，求点F的坐标；

(4)、若M（m，n）是直线BC上方抛物线上一点，如果△MBC为锐角三角形，请直接写出点M的横坐标m的取值范围.

查看试题解析
27. 如图所示，已知BC是水平面，AB、AD、CD是斜坡.AB的坡角为42°，坡长为200米，AD的坡角为60°，坡长为100米，CD的坡比 $i = 1 ： 2 \sqrt{2}$ .

(1)、求坡顶A到水平面BC的距离；

(2)、求斜坡CD的长度.（结果精确到1米，参考数据： $\sin 42 ° \approx 0.70$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
28. 将 $△ A B C$ 绕点A按逆时针方向旋转 $θ$ 度，并使各边长变为原来的n倍，得 $△ A B^{'} C^{'}$ ，如图①，我们将这种变换记为 $[θ ， n]$ .

(1)、如图①，对 $△ A B C$ 作变换 $[40 ° ， \sqrt{7}]$ 得 $△ A B^{'} C^{'}$ ，则 $S_{△ A B^{'}}_{C^{'}} ： S_{△ A B C} =$ ；直线 $B C$ 与直线 $B^{'} C^{'}$ 所夹的锐角为度；

(2)、如图②， $△ A B C$ 中， $∠ B A C = 30 ° ， ∠ A C B = 90 °$ ，对 $△ A B C$ 作变换 $[θ ， n]$ 得 $△ A B^{'} C^{'}$ ，使点B、C、 $C^{'}$ 在同一直线上，且四边形 $A B B^{'} C^{'}$ 为矩形，求 $θ$ 和n的值；

(3)、如图③， $△ A B C$ 中， $A B = A C ， ∠ B A C = 36 ° ， B C = 2$ ，对 $△ A B C$ 作变换 $[θ ， n]$ 得 $△ A B^{'} C^{'}$ ，使点B、C、 $B^{'}$ 在同一直线上，且四边形 $A B B^{'} C^{'}$ 为平行四边形，求 $θ$ 和n的值.

查看试题解析