2022年江苏省泰州市中考数学模拟卷1
试卷更新日期:2022-04-14 类型:中考模拟
一、单选题(每题3分,共18分)
-
1. 计算30的结果是( )A、3 B、30 C、1 D、02. 如图所示的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、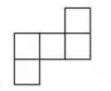 D、
D、 3. 下列二次根式与 是同类二次根式的是( )A、 B、 C、 D、4. 任意一个事件发生的概率p的取值范围是( )A、0<P<1 B、0≤P<1 C、0<P≤1 D、0≤p≤15. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
3. 下列二次根式与 是同类二次根式的是( )A、 B、 C、 D、4. 任意一个事件发生的概率p的取值范围是( )A、0<P<1 B、0≤P<1 C、0<P≤1 D、0≤p≤15. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )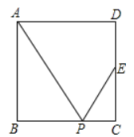 A、 B、 C、是的中点 D、6. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或3
A、 B、 C、是的中点 D、6. 已知线段 ,在直线AB上作线段BC , 使得 .若D是线段AC的中点,则线段AD的长为( )A、1 B、3 C、1或3 D、2或3二、填空题(每题3分,共30分)
-
7. 若一个数的相反数是-7,则这个数为 .8. 在函数 中,自变量 的取值范围是.9. 2022年2月4日,第24届冬奥会在北京开幕,中国大陆地区观看开幕式的人数约316000000人,请把316000000用科学记数法表示出来 .10. 已知点、为函数的图象上的两点,若 , 则(填“>”、“=”或“<”).11. 一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,则第5组的频率为 .12. 若一元二次方程的两根分别为m与n,则 .13. 若扇形的圆心角为60°,半径为2,则该扇形的弧长是(结果保留)14. 如图, ABC中,∠C=72°,AB边的垂直平分线交AB于点D,交AC于点E,将 ABE沿BE翻折得到 ,若 ,则∠ABC=.
 15. 如图,已知在Rt△AOB中,∠AOB=90°,⊙O与AB相交于点C,与BO相交于点D,连结CD,CO.若∠BOC=2∠BCD,AO=15,AB=25,则BD的长是
15. 如图,已知在Rt△AOB中,∠AOB=90°,⊙O与AB相交于点C,与BO相交于点D,连结CD,CO.若∠BOC=2∠BCD,AO=15,AB=25,则BD的长是 16. 如图,在中,中线相交于点 , 如果的面积是4,那么四边形的面积是
16. 如图,在中,中线相交于点 , 如果的面积是4,那么四边形的面积是
三、解答题(共10题,共102分)
-
17.(1)、因式分解:(y+2x)2-(x+2y)2(2)、先化简,再求值:(1)÷ , 其中m=.18. 双减背景下,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名初中学生,根据调查结果得到如图所示的统计图表.
类别
时间 (小时)
人数
A
5
B
20
C
D
30
E
10

请根据图表信息解答下列问题:
(1)、求 的值.(2)、补全条形统计图.(3)、小王说:“我每天的锻炼时间是调查所得数据的中位数”,问小王每天进行体育锻炼的类别是哪类?(4)、据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.19. 2022年冬奥会将在我国北京和张家口举行,如图所示为冬奥会和冬残奥会的会徽“冬梦”“飞跃”,吉样物“冰墩墩”“雪容融”,将四张正面分别印有以上个图案的卡片(卡片的形状、大小、质地都相同)背面朝上洗匀. (1)、若从中任意抽取1张,抽得卡片上的图案恰好为“冰墩墩”的概率是 .(2)、若从中任意抽取两张,请用列表或画树状图法求两张卡片上的图案都是会徽的概率.20. 某厂生产甲、乙两种型号的产品,生产1个甲种产品需要用时2分钟、耗材30克;生产1个乙种产品需要用时3分钟、耗材40克.如果生产甲产品和生产乙产品共用时 小时、耗材11千克,那么甲、乙两种产品各生产多少个?21. 如图,小马同学在数学综合实践活动中,利用所学的数学知识对山坡一棵树的高度进行测量,先测得小马同学离底部 的距离 为10m,此时测得对树的顶端 的仰角为55°,已知山坡与水平线的夹角为20°,小马同学的观测点 距地面1.6m,求树木 的高度(精确到0.1m).(参考数据: , , , , , ).
(1)、若从中任意抽取1张,抽得卡片上的图案恰好为“冰墩墩”的概率是 .(2)、若从中任意抽取两张,请用列表或画树状图法求两张卡片上的图案都是会徽的概率.20. 某厂生产甲、乙两种型号的产品,生产1个甲种产品需要用时2分钟、耗材30克;生产1个乙种产品需要用时3分钟、耗材40克.如果生产甲产品和生产乙产品共用时 小时、耗材11千克,那么甲、乙两种产品各生产多少个?21. 如图,小马同学在数学综合实践活动中,利用所学的数学知识对山坡一棵树的高度进行测量,先测得小马同学离底部 的距离 为10m,此时测得对树的顶端 的仰角为55°,已知山坡与水平线的夹角为20°,小马同学的观测点 距地面1.6m,求树木 的高度(精确到0.1m).(参考数据: , , , , , ). 22. 如图,在平面直角坐标系中,菱形OABC的边OC在x轴上,B(18,6),反比例函数 的图象经过点A,与OB交于点E.
22. 如图,在平面直角坐标系中,菱形OABC的边OC在x轴上,B(18,6),反比例函数 的图象经过点A,与OB交于点E. (1)、求菱形OABC的边长;(2)、求出k的值;(3)、求OE:EB的值.23. 阅读下面材料,并解答其后的问题:
(1)、求菱形OABC的边长;(2)、求出k的值;(3)、求OE:EB的值.23. 阅读下面材料,并解答其后的问题:定义:两组邻边分别相等的四边形叫做筝形.
如图1,四边形ABCD中,若AD=AB,CD=CB,则四边形ABCD是筝形.

类比研究:
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对平行四边形的性质进行研究,请根据示例图形,完成下表:
四边形
示例图形
对称性
边
角
对角线
平行
四边形

是中心对称图形
两组对边分别平行,两组对边分别相等.
两组对角
分别相等.
对角线互相平分.
筝形

①
两组邻边分别相等
有一组对角相等
②
(1)、表格中①、②分别填写的内容是:①;
②.
(2)、演绎论证:证明筝形有关对角线的性质.如图2,已知:在筝形ABCD中,AD=AB,BC=DC,AC、BD是对角线.
求证: ▲ .
证明:
(3)、运用:如图3,已知筝形ABCD中,AD=AB=4,CD=CB,∠A=90°,∠C=60°,求筝形ABCD的面积.24. 某商贸公司购进某种商品的成本为20元/千克,经过市场调研发现,这种商品在未来40天的销售单价y(元/千克)与时间×(天)之间的函数关系式为:y= ,且×为整数,且日销量m(千克)与时间×(天)之间的变化规律符合一次函数关系,如下表:时间x(天)
1
3
6
10
……
日销量m(千克)
142
138
132
124
……
(1)、求m与×的函数关系式;(2)、当1≤×≤20时,最大日销售利润是多少?(3)、求:在未来40天中,有多少天销售利润不低于1550元?25. 已知抛物线y=ax2+bx+c(a≠0)的顶点在×轴上. (1)、若抛物线过点P(0, ),求证:a=b2?;(2)、已知点P1(-2,1),P2(2,-1),P3(2,1)中恰有两点在抛物线上
(1)、若抛物线过点P(0, ),求证:a=b2?;(2)、已知点P1(-2,1),P2(2,-1),P3(2,1)中恰有两点在抛物线上①求抛物线的解析式;
②设直线l:y= x+1与抛物线交于A,B两点,点M在直线y=n(n<0)上,过A,B两点分别作直线y=n(n<0)的垂线,垂足为C,D.是否存在这样的n的值,使得以点A,C,M为顶点的三角形与△BDM相似的点M恰有两个?若存在,请直接写出n的值;若不存在,请说明理由.
26. 如图1,四边形ABCD内接于 , 对角线 AC 是的直径,AB,DC 的延长线交于点E,.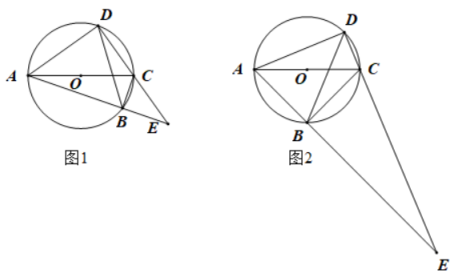 (1)、求证:是等腰三角形;(2)、如图2,若BD平分 , 求的值;(3)、如图1,若 , , 求y与x的函数关系式.
(1)、求证:是等腰三角形;(2)、如图2,若BD平分 , 求的值;(3)、如图1,若 , , 求y与x的函数关系式.