2022年江苏省常州市中考数学模拟卷1

试卷更新日期：2022-04-13 类型：中考模拟

进入出卷网下载

一、单选题（每题2分，共16分）

1. 2022的相反数的倒数是（）

A、2022 B、 $- \frac{1}{2022}$ C、 $\frac{1}{2022}$ D、-2022

查看试题解析
2. ${(a^{3})}^{2}$ 的值是（）

A、 $a^{6}$ B、 $a^{5}$ C、 $a^{9}$ D、 $- a^{6}$

查看试题解析
3. 如图是某几何体的三视图，这个几何体可以是（）

A、 B、 C、 D、

查看试题解析
4. 剪纸艺术是第一批国家级非物质文化遗产，下列图案既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，AB是⊙O的直径，CD是弦，若∠BCD=36°，则∠ABD等于（）

A、36° B、54° C、64° D、72°

查看试题解析
6. 如图①所示，平整的地面上有一个不规则图案（图中阴影部分），为了了解该图案的面积是多少，我们采取了以下办法：用一个长为a，宽为b的长方形，将不规则图案围起来，然后在适当位置随机地朝长方形区域扔小球，并记录小球落在不规则图案上的次数（球扔在界线上或长方形区域外不计实验结果），现将若干次有效实验的结果绘制成了如图②所示的折线统计图，由此估计不规则图案的面积大约是（）

A、 $\frac{3}{10}$ a² B、 $\frac{7}{20}$ ab C、 $\frac{2}{5}$ b² D、 $\frac{13}{40}$ ab

查看试题解析
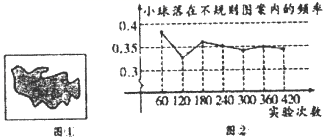7. 下列关于二次函数y＝2x²的说法正确的是（）

A、它的图象经过点（－1，－2） B、它的图象的对称轴是直线x＝2 C、当x＜0时，y随x的增大而增大 D、当－1 $\leq x \leq$ 2时，y有最大值为8，最小值为0

查看试题解析
8. 如图，矩形纸片ABCD中，BC=4，AB=3，点P是BC边上的动点（点P不与点B、C重合）．现将△PCD沿PD翻折，得到△PC′D ，作∠BPC′的角平分线，交AB于点E ．设BP=x ， BE=y ，则下列图象中，能表示y与x的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题（每题2分，共20分）

9. 4的平方根是；8的立方根是.

查看试题解析
10. 要使多项式 $x^{2} - \frac{1}{2} m x y + 7 y^{2} + x y - x + 1$ 中不含 $x y$ 项，那么 $m$ =

查看试题解析
11. 因式分解： $9 a - 4 a^{3} =$ .

查看试题解析
12. 2020年政府工作报告会中提出，优化投资结构，发挥政府投资撬动作用，引导更多资金投向强基础、增后劲、惠民生领域，新建、改建农村公路1270000公里，其中1270000用科学记数法表示为.

查看试题解析
13. 若x＜2，且 $\frac{1}{x - 2} + | x - 2 | + x - 1 = 0$ ，则x＝．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $A B = 8$ ， $D E ⊥ A B$ ，垂足为E， $B E = 6$ ，连接 $C E$ ，若 $∠ C E B = ∠ A D E$ ，则 $D E =$ ．

查看试题解析
15. 如图，在△ABC中，∠B=25°，点D是BC边上一点，连接AD，且AD = BD，∠CAD =∠90°，CF平分∠ACB，分别交AD，AB于点E，F，则∠AEC的度数为.

查看试题解析
16. 如图，在平面直角坐标系中，点A和B的坐标分别为（2，0），（0，-4），若将线段AB绕点A顺时针旋转90°得到线段AC，则点C的坐标为

查看试题解析
17. 如图，已知正方形ABCD，延长AB至点E使BE＝AB，连接CE、DE，DE与BC交于点N，取CE的中点F，连接BF，AF，AF交BC于点M，交DE于点O，则下列结论：①DN＝EN；②OA＝OE；③tan∠CED $= \frac{1}{3}$ ；④S_{四边形BEFM}＝2S_△_CMF ．其中正确的是.（只填序号）

查看试题解析
18. 如图，在等腰 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = B C = 4 \sqrt{2}$ .点 $D$ 和点 $E$ 分别在 $B C$ 边和 $A B$ 边上，连接 $D E$ .将 $△ B D E$ 沿 $D E$ 折叠，得到 $△ B^{^{'}} D E$ ，点 $B$ 恰好落在 $A C$ 的中点处.设 $D E$ 与 $B B^{'}$ 交于点 $F$ ，则 $D E =$ .

查看试题解析

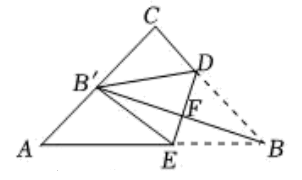
三、解答题（共10题，共84分）

19. 计算：2^﹣1+4cos45° $- \sqrt{8} +$ （π﹣2022）⁰ ．

查看试题解析
20.

(1)、解方程： $x^{2} - 4 x - 5 = 0$

(2)、解不等式组： ${\begin{matrix} 2 x - 1 \leq 3 \\ x + 2 > 3 x + 8 \end{matrix}$

查看试题解析
21. 某校要加强中小学生作业、睡眠、手机、读物、体质管理．数学社团成员采用随机抽样的方法，抽取了七年级若干名学生，对他们一周内平均每天的睡眠时间t（单位：h）进行了调查，将数据整理后得到下列不完整的统计图表和扇形统计图：
请根据图表信息回答下列问题：

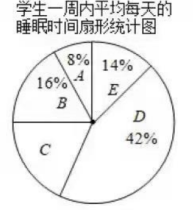
(1)、本次被抽取的七年级学生共有名；

(2)、统计图表中，m＝；

(3)、扇形统计图中，C组所在扇形的圆心角的度数是°；

(4)、请估计该校800名七年级学生中睡眠不足7小时的人数．

查看试题解析
22. 在一个不透明的袋子中，放有四张质地完全相同的卡片，分别标有数字“ $- 3 ， - 2 ， 1 ， 6$ ”．

(1)、随机抽出一张卡片是负数的概率是；

(2)、第一次从袋中随机地抽出一张卡片，把所抽到的数字记为横坐标 $m$ ，不放回袋中，再随机地从中抽出一张，把所抽到的数字记为纵坐标 $n$ ．请用数状图或列表法求所得的点 $(m ， n)$ 在反比例函数 $y = \frac{6}{x}$ 上的概率．

查看试题解析
23. 如图，四边形ABCD是平行四边形，O是对角线AC的中点，过点O的直线分别交边BC，AD于点E，F，连结AE，CF.

(1)、求证：△AOF≌△COE；

(2)、当∠OAF＝∠OFA时，求证：四边形AECF是矩形.

查看试题解析
24. 永州市某村经济合作社在乡村振兴工作队的指导下，根据市场需求，计划在2022年将30亩土地全部用于种植A、B两种经济作物.预计B种经济作物亩产值比A种经济作物亩产值多2万元，为实现2022年A种经济作物年总产值20万元，B种经济作物年总产值30万元的目标，问：2022年A、B两种经济作物应各种植多少亩？

查看试题解析
25. 如图，一次函数y=kx+b(k>0)的图象经过点C(−3，0)，且与两坐标轴围成的三角形的面积为3.

(1)、求一次函数的解析式；

(2)、若反比例函数 $y = \frac{m}{x}$ 的图象与该一次函数的图象交于一、三象限内的A，B两点，且AC=2BC，求m的值.

查看试题解析
26. 有一组对边平行，一个内角是它对角的两倍的四边形叫做倍角梯形.

(1)、已知四边形ABCD是倍角梯形，AD∥BC，∠A＝100°，请直接写出所有满足条件的∠D的度数；

(2)、如图1，在四边形ABCD中，∠BAD+∠B＝180°，BC＝AD+CD.求证：四边形ABCD是倍角梯形；

(3)、如图2，在（2）的条件下，连结AC，当AB＝AC＝AD＝2时，求BC的长.

查看试题解析
27. 我们定义：如果关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0$ 有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”．

(1)、请说明方程 $x^{2} - 3 x + 2 = 0$ 是倍根方程；

(2)、若 $(x - 2) (m x + n) = 0$ 是倍根方程，则 $m$ ， $n$ 具有怎样的关系？

(3)、若一元二次方程 $a x^{2} + b x + c = 0 (b^{2} - 4 a c \geq 0)$ 是倍根方程，则 $a$ ， $b$ ， $c$ 的等量关系是（直接写出结果）

查看试题解析
28. 如图，已知；抛物线y= $\frac{1}{4}$ x²+bx+c经过点A（0，2），点C（4，0），且交x轴于另一点B．

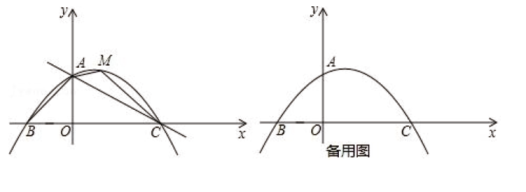(1)、求抛物线的解析式；

(2)、在直线AC上方的抛物线上有一点M，求三角形ACM面积的最大值及此时点M的坐标；

(3)、将线段OA绕x轴上的动点P（m，0）顺时针旋转90°得到线段O'A'，若线段O'A’与抛物线只有一个公共点，请结合函数图象，求m的取值范围．

查看试题解析