2022年初中数学苏科版《中考二轮复习》专题一 数与式、方程与不等式 1.7 不等式
试卷更新日期:2022-04-13 类型:二轮复习
一、单选题
-
1. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,数轴上点 、 对应的数分别为 、 ,则下列不等式正确的是( )
2. 如图,数轴上点 、 对应的数分别为 、 ,则下列不等式正确的是( )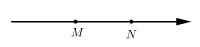 A、 B、 C、 D、3. 若实数 a 是不等式 2x-1>5 的解,但实数 b 不是不等式 2x-1>5 的解,则下列选项中,正确的是( )A、a<b B、a>b C、a≤b D、a≥b4. 某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为( )A、10 B、9 C、8 D、75. 若不等式组 有解,则a的取值范围是 ( )A、a>-1 B、a≥-1 C、a≤1 D、a<16. 若关于x的一元一次不等式组 的解集是x a,且关于y的分式方程 有非负整数解,则符合条件的所有整数a的和为( )A、0 B、1 C、4 D、67. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、8. 从﹣3,﹣1, ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组 无解,且使关于x的分式方程 ﹣ =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )A、﹣3 B、﹣2 C、﹣ D、9. 对于实数x,规定[x]表示不大于x的最大整数,例如[1.2]=1,[﹣2.5]=﹣3,若[x﹣2]=﹣1,则x的取值范围为( )A、0<x≤1 B、0≤x<1 C、1<x≤2 D、1≤x<210. 运行程序如图所示,从“输入实数 x”到“结果是否<18”为一次程序操作,若输入 x 后程序操作仅进行了三次就停止,那么 x 的取值范围是( )
A、 B、 C、 D、3. 若实数 a 是不等式 2x-1>5 的解,但实数 b 不是不等式 2x-1>5 的解,则下列选项中,正确的是( )A、a<b B、a>b C、a≤b D、a≥b4. 某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为( )A、10 B、9 C、8 D、75. 若不等式组 有解,则a的取值范围是 ( )A、a>-1 B、a≥-1 C、a≤1 D、a<16. 若关于x的一元一次不等式组 的解集是x a,且关于y的分式方程 有非负整数解,则符合条件的所有整数a的和为( )A、0 B、1 C、4 D、67. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、8. 从﹣3,﹣1, ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组 无解,且使关于x的分式方程 ﹣ =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )A、﹣3 B、﹣2 C、﹣ D、9. 对于实数x,规定[x]表示不大于x的最大整数,例如[1.2]=1,[﹣2.5]=﹣3,若[x﹣2]=﹣1,则x的取值范围为( )A、0<x≤1 B、0≤x<1 C、1<x≤2 D、1≤x<210. 运行程序如图所示,从“输入实数 x”到“结果是否<18”为一次程序操作,若输入 x 后程序操作仅进行了三次就停止,那么 x 的取值范围是( )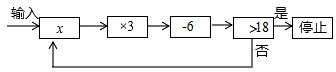 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知关于x的不等式(1-a)x>3的解集为 则a的取值范围是 .12. 在平面直角坐标系中,若点 在第二象限,则整数m的值为.13. 若不等式组 的解集为-1<x<1,那么(a+1)(b-1)的值等于 .14. 如果关于x的方程x2+2(a+1)x+2a+1=0有一个小于2的正数根,那么实数a的取值范围是.15. 从-3,-2,-1,0,2,3这七个数中,随机取出一个数,记为a,那么a使关于x的方程 有整数解,且使关于x的不等式组 有解的概率为.16. 已知 是负整数,关于 的一元二次方程 的两根是 、 ,若 ,则 的值等于.17. 任何实数a,可用[a]表示不超过a的最大整数,如[2]=2,[3.7]=3,现对72进行如下操作:
,这样对72只需进行3次操作后变为1,类似地:对109只需进行次操作后变为1.
18. 对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n﹣ ≤x<n+ ,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:
①(1.493)=1;②(2x)=2(x);③若( )=4,则实数x的取值范围是9≤x<11;④当x≥0,m为非负整数时,有(m+2013x)=m+(2013x);⑤(x+y)=(x)+(y);其中,正确的结论有(填写所有正确的序号).
三、解答题
-
19. 解不等式组:(1)、(2)、20. 若数 使关于 的分式方程 的解为正数,且使关于 的不等式组 的解集为 ,求符合条件的所有整数 的和.21. 某地为引导旅客来旅游及消费,计划5月至9月开展全城推广活动.某旅行社为吸引市民组团去旅游,推出了如下收费标准:如果人数不超过25人,人均旅游费用为2000元;如果超过25人,每增加1人,人均旅游费用降低40元,但人均旅游费用不得低于1700元.某单位组织员工去旅游,共支付给该旅行社旅游费用54000元,请问该单位这次共有多少员工去旅游?22. 对于三个数 、 、 ,用 表示这三个数的中位数,用 表示这三个数中最大数,例如: , , .
解决问题:
(1)、填空:如果 ,则 的取值范围为;(2)、如果 ,求 的值.23. 自学下面材料后,解答问题.分母中含有未知数的不等式叫分式不等式.如: >0; <0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负.其字母表达式为:
①若a>0,b>0,则 >0;若a<0,b<0,则 >0;
②若a>0,b<0,则 <0;若a<0,b>0,则 <0·
(1)、反之:①若 >0,则 或 ;②若 <0,则 .
(2)、根据上述规律,求不等式 >0的解集.24. 深化理解:新定义:对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果n﹣ ≤x<n+ ,则<x>=n;
反之,当n为非负整数时,如果<x>=n,则n﹣ ≤x<n+ .
例如:<0>=<0.48>=0,<0.64>=<1.49>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)、填空:①<π>=(π为圆周率); ②如果<x﹣1>=3,则实数x的取值范围为 .(2)、若关于x的不等式组 的整数解恰有3个,求a的取值范围.(3)、求满足<x>= x 的所有非负实数x的值.25. 为了迎接“五.一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元,售价320元;乙种服装每件进价150元,售价280元·(1)、若该专卖店同时购进甲、乙两种服装共200件,恰好用去32 400元,求购进甲、乙两种服装各多少件?(2)、该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26 700元,且不超过26 800元,则该专卖店有几种进货方案?(3)、在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变,那么该专卖店要获得最大利润应如何进货?26. 为了解都匀市交通拥堵情况,经统计分析,都匀彩虹桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度为20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)、求彩虹桥上车流密度为100辆/千米时的车流速度;(2)、在交通高峰时段,为使彩虹桥上车流速度大于40千米/小时且小于60千米/小时,应控制彩虹桥上的车流密度在什么范围内?(3)、当车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.当20≤x≤220时,求彩虹桥上车流量y的最大值.27. 由 得, ;如果两个正数a,b,即 , 则有下面的不等式: , 当且仅当 时取到等号.例如:已知 , 求式子 的最小值.
解:令 , 则由 , 得 , 当且仅当 时,即 时,式子有最小值,最小值为4.
请根据上面材料回答下列问题:
(1)、当 , 式子 的最小值为;当 , 则当 时,式子 取到最大值;(2)、用篱笆围一个面积为32平方米的长方形花园,使这个长方形花园的一边靠墙(墙长20米),问这个长方形的长、宽各为多少时,所用的篱笆最短,最短的篱笆是多少?
 (3)、如图,四边形 的对角线 、 相交于点O, 、 的面积分别是8和14,求四边形 面积的最小值.
(3)、如图,四边形 的对角线 、 相交于点O, 、 的面积分别是8和14,求四边形 面积的最小值.
 28. 学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.
28. 学校数学兴趣小组利用机器人开展数学活动.在相距 个单位长度的直线跑道 上,机器人甲从端点 出发,匀速往返于端点 、 之间,机器人乙同时从端点 出发,以大于甲的速度匀速往返于端点 、 之间.他们到达端点后立即转身折返,用时忽略不计.兴趣小组成员探究这两个机器人迎面相遇的情况,这里的“迎面相遇”包括面对面相遇、在端点处相遇这两种.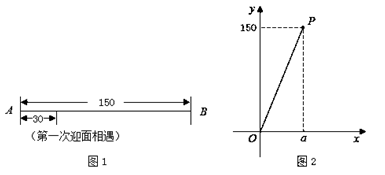 (1)、【观察】
(1)、【观察】①观察图 ,若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
②若这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,则他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度;
(2)、【发现】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第二次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.兴趣小组成员发现了 与 的函数关系,并画出了部分函数图象(线段 ,不包括点 ,如图 所示).
① =;
②分别求出各部分图象对应的函数表达式,并在图 中补全函数图象;
(3)、【拓展】设这两个机器人第一次迎面相遇时,相遇地点与点 之间的距离为 个单位长度,他们第三次迎面相遇时,相遇地点与点 之间的距离为 个单位长度.若这两个机器人第三次迎面相遇时,相遇地点与点 之间的距离 不超过 个单位长度,则他们第一次迎面相遇时,相遇地点与点 之间的距离 的取值范围是.(直接写出结果)