2022年初中数学苏科版《中考二轮复习》专题一 数与式、方程与不等式 1.6 二元一次方程
试卷更新日期:2022-04-13 类型:二轮复习
一、单选题
-
1. 如果2xa﹣2b﹣3ya+b+1=0是二元一次方程,那么a,b的值分别是( )A、1,0 B、0,1 C、﹣1,2 D、2,﹣12. 《孙子算经》中有一道题,原文是“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺.问木长多少尺?设木长x尺,绳长y尺,可列方程组为( )A、 B、 C、 D、3. 在△ABC中,∠A,∠B均为锐角,且有|tanB﹣ |+(2cosA﹣1)2=0,则△ABC是( )A、直角(不等腰)三角形 B、等边三角形 C、等腰(不等边)三角形 D、等腰直角三角形4. 若实数a、b满足 ,则 的值是( )A、1 B、-1 C、3 D、-35. 小明解方程组x+y=■的解为x=5,由于不小心滴下了两滴墨水,刚好把 两个数■和★遮住了,则这个数■和★的值为( )A、 B、 C、 D、6. 如果方程组 与 有相同的解,则a,b的值是( )A、
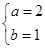 B、
B、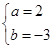 C、
C、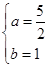 D、
D、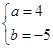 7. 已知点P(m,n)在直线y=﹣x+2上,双曲线y= (k为常数)图象经过点P,则2021m2﹣2020n2+2019k2的值是( )A、4040 B、2020 C、﹣1 D、18. 小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )
7. 已知点P(m,n)在直线y=﹣x+2上,双曲线y= (k为常数)图象经过点P,则2021m2﹣2020n2+2019k2的值是( )A、4040 B、2020 C、﹣1 D、18. 小明出门时身上带了100元,下表记录了他今天所有支出,其中饮料与饼干支出的金额被涂黑.若每瓶饮料5元,每包饼干8元,则小明不可能剩下多少元?( )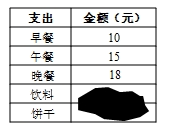 A、4 B、15 C、22 D、449. 《九章算术》是我国东汉年间编订的一部数学经典著作,在它的“方程”一章里一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,把它改为横排,如图(1)、(2),图中各行从左到右列出的算筹数分别表示未知数x,y的系数与对应的常数项,把图(1)所示的算筹图中方程组形式表述出来,就是 ,类似地,图(2)所示的算筹图可表述为( )
A、4 B、15 C、22 D、449. 《九章算术》是我国东汉年间编订的一部数学经典著作,在它的“方程”一章里一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,把它改为横排,如图(1)、(2),图中各行从左到右列出的算筹数分别表示未知数x,y的系数与对应的常数项,把图(1)所示的算筹图中方程组形式表述出来,就是 ,类似地,图(2)所示的算筹图可表述为( ) A、 B、 C、 D、10. 已知关于x、y的方程组 ,给出下列说法:
A、 B、 C、 D、10. 已知关于x、y的方程组 ,给出下列说法:①当a =1时,方程组的解也是方程x+y=2的一个解;②当x-2y>8时, ;③不论a取什么实数,2x+y的值始终不变;④若 ,则 。 以上说法正确的是( )
A、②③④ B、①②④ C、③④ D、②③二、填空题
-
11. 如果二元一次方程组 的解是 ,则a﹣b=12. 若关于x、y的二元一次方程组 的解满足x+y>0,则m 的取值范是 .13. 同学们每个星期都会听着国歌升国旗,但国歌歌词有多少个字可能大家都不知道.已知歌词数量是一个两位数,十位数是个位数的两倍,且十位数比个位数大4,则国歌歌词数有个.14. 一个两位数,个位上的数比十位上的数的2倍多1,将十位数字与个位数字调换位置,则比原来两位数的2倍还多2,设原两位数个位数字为x,十位数字为y,则这个两位数为:
15. 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是cm. 16. 现有八个大小相同的长方形,可拼成如图①、②所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,则每个小长方形的面积是 .
16. 现有八个大小相同的长方形,可拼成如图①、②所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,则每个小长方形的面积是 . 17. 规定:用{m}表示大于m的最小整数,例如 =3,{5}=6,{-1.3}=-1等;用[m]表示不大于m的最大整数,例如 =3,[4]=4,[-1.5]=-2,如果整数x满足关系式:2{x}+3[x]=12,则x=.18. 三个同学对问题“若方程组的 解是 ,求方程组 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
17. 规定:用{m}表示大于m的最小整数,例如 =3,{5}=6,{-1.3}=-1等;用[m]表示不大于m的最大整数,例如 =3,[4]=4,[-1.5]=-2,如果整数x满足关系式:2{x}+3[x]=12,则x=.18. 三个同学对问题“若方程组的 解是 ,求方程组 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .三、解答题
-
19. 解方程组:(1)、(2)、20. 已知xyz≠0,且x+2y+z=0,5x+4y-4z=0,求 的值21. 百脑汇商场中路路通商店有甲、乙两种手机内存卡,买2个甲内存卡和1个乙内存卡用了90元,买3个甲内存卡和2个乙内存卡用了160元.(1)、求甲、乙两种内存卡每个各多少元?(2)、如果小亮准备购买甲.乙两种手机内存卡共10个,总费用不超过350元,且不低于300元,问有几种购买方案,哪种方案费用最低?(3)、某天,路路通售货员不小心把当天上午卖的甲、乙种手机内存卡的销售量统计单丢失了,但老板记得每件甲内存卡每个赚10元,乙内存卡每个赚15元,一上午售出的内存卡共赚了100元,请你帮助老板算算有几种销售方案?并直接写出销售方案.22. 某植物园现有A,B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x-y)米;B园区为正方形,边长为(x+2y)米。(1)、请用代数式表示A,B两园区的面积之和并化简;(2)、现根据实际需要对A园区进行整改,长增加(4x-y)米,宽减少(x-2y)米,整改后A园区的长比宽多190米,且整改后两园区的周长之和为660米。
①求x,y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C,D两种花投入的费用与吸引游客的收益如下表:
C
D
投入(元/平方米)
16
12
收益(元/平方米)
26
18
求整改后A,B两园区旅游的净利润之和.(净利润=收益-投入)
23. 商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.24. 随着“互联网+”时代的到来,传统的教学模式也在悄然发生着改变.某出国培训机构紧跟潮流,对培训课程采取了线上线下同步销售的策路,为了让客户更理性的选择,该机构推出了甲、乙两个课程体验包:甲课程体验包价值660元含3节线上课程和2节线下课;乙课程体验包价值990元含2节线上课程和5节线下课程.(1)、分别求出该机构每节课的线上价格和线下价格;(2)、该机构其中一个销售团队上个月的销售业绩为:线上课程成交900节,线下课成交1000节.为回馈客户,本月该机构针对线上、线下每节课程的价格均作出了调整:每节课线上价格比上个月的价格下调a%,线下价格比上个月的价格下调 a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了 a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.25. 某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.(1)、求购进甲、乙两种花卉,每盆各需多少元?(2)、该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;(3)、在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?26. “保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型公交车x辆,完成下表:数量(辆)
购买总费用(万元)
载客总量(万人次)
A型车
x
60x
B型车
(3)、若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用最少?最少总费用是多少?