北师大版备考2022中考数学二轮复习专题9 平面直角坐标系与函数
试卷更新日期:2022-04-13 类型:二轮复习
一、单选题
-
1. 下面四个关系式:① ;② ;③ ;④ .其中 是 的函数的是( )A、①② B、②③ C、①②③ D、①③④2. 小莹和小博下棋,小莹执白,小博执黑.如图所示,棋盘中心黑子的位置用( - 1,0)表示,右下角黑子的位置用(0, - 1)表示.小莹将第4枚白子放人棋盘后,所有棋子构成一个轴对称图形,她放的位置是( )
 A、( - 2,1) B、( - 1,1) C、(1, - 2) D、( - 1, - 2)3. 定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )A、2个 B、3个 C、4个 D、5个4. 如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
A、( - 2,1) B、( - 1,1) C、(1, - 2) D、( - 1, - 2)3. 定义:平面内的直线l1与l2相交于点O,对于该平面内任意一点M,点M到直线l1、l2的距离分别为a、b,则称有序非负实数对(a,b)是点M的“距离坐标”,根据上述定义,距离坐标为(2,1)的点的个数有( )A、2个 B、3个 C、4个 D、5个4. 如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )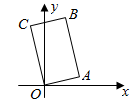 A、 B、3 C、 D、55. 如图,平面直角坐标系中,一蚂蚁从 点出发,沿着 循环爬行,其中 点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 ,当蚂蚁爬了 个单位时,蚂蚁所处位置的坐标为( )
A、 B、3 C、 D、55. 如图,平面直角坐标系中,一蚂蚁从 点出发,沿着 循环爬行,其中 点的坐标为 , 点的坐标为 , 点的坐标为 , 点的坐标为 ,当蚂蚁爬了 个单位时,蚂蚁所处位置的坐标为( ) A、 B、 C、 D、6. 如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y(厘米)与注水时间x(秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是( )
A、 B、 C、 D、6. 如图①,一个立方体铁块放置在圆柱形水槽内,现以每秒固定的流量往水槽中注水,28秒时注满水槽,水槽内水面的高度y(厘米)与注水时间x(秒)之间的函数图象如图②所示,则圆柱形水槽的容积(在没放铁块的情况下)是( )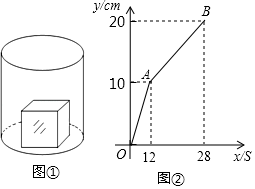 A、8000cm3 B、10000 cm3 C、2000πcm3 D、3000πcm37. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、……,根据这个规律,第2019个点的坐标为( )
A、8000cm3 B、10000 cm3 C、2000πcm3 D、3000πcm37. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序为(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2)、……,根据这个规律,第2019个点的坐标为( ) A、(45,10) B、(45,6) C、(45,22) D、(45,0)8. 在平面直角坐标系中,已知 , ,若点 在第一象限,且 为等腰直角三角形,则正确所有点 的 值之和是( )A、 B、 C、 D、9. 如图, 边长为 的等边三角形 的顶点 分别在边 , 上当 在边 上运动时, 随之在边 上运动,等边三角形的形状保持不变,运动过程中,点 到点 的最大距离为( )
A、(45,10) B、(45,6) C、(45,22) D、(45,0)8. 在平面直角坐标系中,已知 , ,若点 在第一象限,且 为等腰直角三角形,则正确所有点 的 值之和是( )A、 B、 C、 D、9. 如图, 边长为 的等边三角形 的顶点 分别在边 , 上当 在边 上运动时, 随之在边 上运动,等边三角形的形状保持不变,运动过程中,点 到点 的最大距离为( )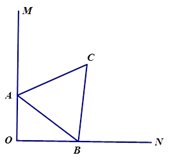 A、 B、 C、 D、10. 如图,在平面直角坐标系中,点A1 , A2 , A3在直线y= x+b上,点B1 , B2 , B3在x轴上,△OA1B1 , △B1A2B2 , △B2A3B3都是等腰直角三角形,若已知点A1(1,1),则点A3的纵坐标是( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,点A1 , A2 , A3在直线y= x+b上,点B1 , B2 , B3在x轴上,△OA1B1 , △B1A2B2 , △B2A3B3都是等腰直角三角形,若已知点A1(1,1),则点A3的纵坐标是( )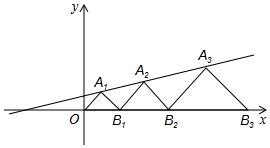 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在平面直角坐标系xOy中,点A(﹣4,0),B(2,0)在x轴上,若点P到两坐标轴的距离相等,且∠APO=∠BPO , 则点P的坐标为 .12. 如图,在平面直角坐标系中,点A的坐标为(0,3),点B的坐标为(6,3).若抛物线y=mx2+2mx+m+3(m为常数,m≠0)向右平移a(a>0)个单位长度,平移后的抛物线的顶点在线段AB上,则a的取值范围为 .
 13. 笔直的海岸线上依次有A , B , C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离 与甲船行驶时间 之间的函数关系如图所示.给出下列说法:①A , B港口相距 ;②乙船的速度为 ;③B , C港口相距 ;④乙船出发 时,两船相距 .其中正确的是(填序号).
13. 笔直的海岸线上依次有A , B , C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离 与甲船行驶时间 之间的函数关系如图所示.给出下列说法:①A , B港口相距 ;②乙船的速度为 ;③B , C港口相距 ;④乙船出发 时,两船相距 .其中正确的是(填序号).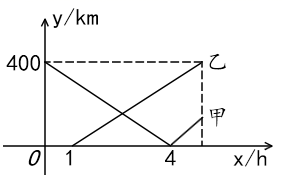 14. 如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为 .
14. 如图,已知A(0,3),B(2,1),C(2,-3),若点P是△ABC三边垂直平分线的交点,则点P的坐标为 .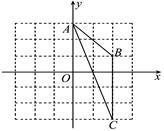 15. 如图所示,在平面直角坐标系内,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1 (0,1),P2(1,1),P3(1,0),P4(1,- 1),P5(2,-1),P6(2,0),……,则点P2021的坐标是
15. 如图所示,在平面直角坐标系内,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1 (0,1),P2(1,1),P3(1,0),P4(1,- 1),P5(2,-1),P6(2,0),……,则点P2021的坐标是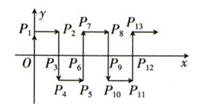 16. 在平面直角坐标系中,A(﹣1,1),B(2,3),C(3m , 4m+1),D在x轴上,若以A , B , C , D四点为顶点的四边形是平行四边形,求点D的坐标.17. 新冠疫情爆发以来,某工厂响应号召,积极向疫情比较严重的甲地区捐赠口罩、消毒液等医疗物资,在工厂装运完物资准备前往甲地的A车与在甲地卸完货准备返回工厂的B车同时出发,分别以各自的速度匀速驶向目的地,出发6小时时A车接到工厂的电话,需要掉头到乙处带上部分检验文件(工厂、甲地、乙在同一直线上且乙在工厂与甲地之间),于是,A车掉头以原速前往乙处,拿到文件后,A车加快速度迅速往甲地驶去,此时,A车速度比B车快32千米/小时,A车掉头和拿文件的时间忽略不计,如图是两车之间的距离y(千米)与B车出发的时间x(小时)之间的函数图象,则当A车到达甲地时,B车离工厂还有千米.
16. 在平面直角坐标系中,A(﹣1,1),B(2,3),C(3m , 4m+1),D在x轴上,若以A , B , C , D四点为顶点的四边形是平行四边形,求点D的坐标.17. 新冠疫情爆发以来,某工厂响应号召,积极向疫情比较严重的甲地区捐赠口罩、消毒液等医疗物资,在工厂装运完物资准备前往甲地的A车与在甲地卸完货准备返回工厂的B车同时出发,分别以各自的速度匀速驶向目的地,出发6小时时A车接到工厂的电话,需要掉头到乙处带上部分检验文件(工厂、甲地、乙在同一直线上且乙在工厂与甲地之间),于是,A车掉头以原速前往乙处,拿到文件后,A车加快速度迅速往甲地驶去,此时,A车速度比B车快32千米/小时,A车掉头和拿文件的时间忽略不计,如图是两车之间的距离y(千米)与B车出发的时间x(小时)之间的函数图象,则当A车到达甲地时,B车离工厂还有千米.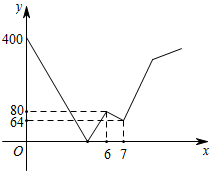 18. 如图,已知 A、B 两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-2,0),半径为2.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是;
18. 如图,已知 A、B 两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-2,0),半径为2.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是;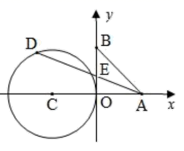
三、作图题
-
19. 探究函数 的图象与性质.
小娜根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
(1)、下表是x与y的几组对应值.x
…
-2
-1
0
1
2
3
…
y
…
-8
-3
0
m
n
1
3
…
请直接写出:m= , n=;
(2)、如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;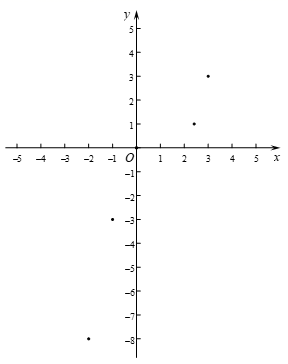 (3)、结合画出的函数图象,解决问题:若方程 有三个不同的解,记为x1 , x2 , x3 , 且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.
(3)、结合画出的函数图象,解决问题:若方程 有三个不同的解,记为x1 , x2 , x3 , 且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.四、解答题
-
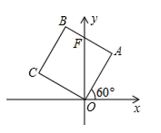
20. 如图正方形OABC的边长等于2,且AO边与x轴正半轴的夹角为60º,O为原点坐标,求点B的坐标.
 21. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
21. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.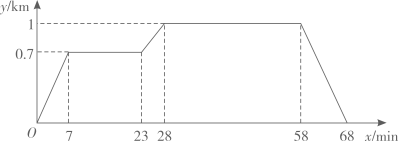
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
0.7
(2)、填空:①食堂到图书馆的距离为 .
②小亮从食堂到图书馆的速度为 .
③小亮从图书馆返回宿舍的速度为 .
④当小亮离宿舍的距离为 时,他离开宿舍的时间为 .
(3)、当 时,请直接写出y关于x的函数解析式.22. 在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D , E , C分别在OA , AB , OB上,OD=2.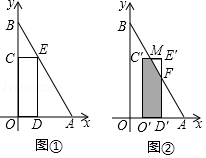
(Ⅰ)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C , O , D , E的对应点分别为C′,O′,D′,E′.设OO′=t , 矩形C′O′D′E′与△ABO重叠部分的面积为S .
①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M , F , 试用含有t的式子表示S , 并直接写出t的取值范围;
②当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
23. 如图,以直角三角形AOC 的直角顶点O为原点,以 OA,OC 所在直线为x轴,y轴建立平面直角坐标系,点 满足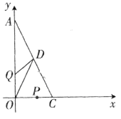 (1)、则 点的坐标为; 点的坐标为.(2)、直角三角形 的面积为.(3)、已知坐标轴上有两动点 同时出发, 点从 点出发沿 轴负方向以1个单位长度每秒的速度匀速移动, 点从 点出发以2个单位长度每秒的速度沿 轴正方向移动,点 到达 点整个运动随之结束. 的中点 的坐标是 ,设运动时间为t(t>0)秒,问:是否存在这样的t使 ?若存在,请求出 的值;若不存在,请说明理由.
(1)、则 点的坐标为; 点的坐标为.(2)、直角三角形 的面积为.(3)、已知坐标轴上有两动点 同时出发, 点从 点出发沿 轴负方向以1个单位长度每秒的速度匀速移动, 点从 点出发以2个单位长度每秒的速度沿 轴正方向移动,点 到达 点整个运动随之结束. 的中点 的坐标是 ,设运动时间为t(t>0)秒,问:是否存在这样的t使 ?若存在,请求出 的值;若不存在,请说明理由.五、综合题
-
24. 已知M、N两地之间有一条240千米长的公路,甲乙两车同时出发,乙车以40千米/时的速度从M地匀速开往N地,甲车从N地沿此公路匀速驶往M地,两车分别到达目的地后停止,甲乙两车相距的路程y(千米)与乙车行驶的时间x(时)之间的函数关系如图所示.
 (1)、甲车速度为千米/时.(2)、求甲乙两车相遇后的y与x之间的函数关系式.(3)、当甲车与乙车相距的路程为140千米时,请直接写出乙车行驶的时间.25. 将两个等腰直角三角形纸片 和 放在平面直角坐标系中,已知点A坐标为 , , , ,并将会 绕点O顺时针旋转.
(1)、甲车速度为千米/时.(2)、求甲乙两车相遇后的y与x之间的函数关系式.(3)、当甲车与乙车相距的路程为140千米时,请直接写出乙车行驶的时间.25. 将两个等腰直角三角形纸片 和 放在平面直角坐标系中,已知点A坐标为 , , , ,并将会 绕点O顺时针旋转.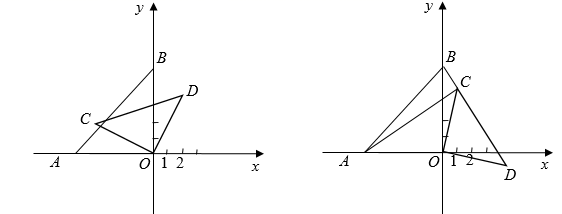 (1)、当旋转至如图①的位置时, ,求此时点C的坐标;(2)、如图②,连接 ,当 旋转到y轴的右侧,且点B , C , D三点在一条直线上时,求 的长;(3)、当旋转到使得 的度数最大时,求 的面积(直接写出结果即可).26. 如图,在平面直角坐标系内有一正方形OABC,点C坐标为(0,4),点D为AB的中点,直线y=- 经过点C,D并交x轴于点E,△BCD沿着CD折叠,顶点B恰好落在OA边上方F处,连接BE,点P为直线CD上的一动点,点Q是线段BE的中点.连接BP,PQ.
(1)、当旋转至如图①的位置时, ,求此时点C的坐标;(2)、如图②,连接 ,当 旋转到y轴的右侧,且点B , C , D三点在一条直线上时,求 的长;(3)、当旋转到使得 的度数最大时,求 的面积(直接写出结果即可).26. 如图,在平面直角坐标系内有一正方形OABC,点C坐标为(0,4),点D为AB的中点,直线y=- 经过点C,D并交x轴于点E,△BCD沿着CD折叠,顶点B恰好落在OA边上方F处,连接BE,点P为直线CD上的一动点,点Q是线段BE的中点.连接BP,PQ.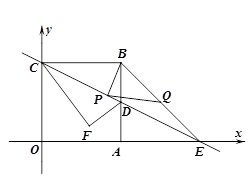 (1)、求点F的坐标;(2)、求出点P运动过程中,PO+PA的最小值;(3)、是否存在点P,使其在运动过程中满足△EQP △EBC,若存在,求出点P坐标;若不存在,请说明理由.27. 如图,直线y=2x-1与x轴、y轴分别交于B、C两点
(1)、求点F的坐标;(2)、求出点P运动过程中,PO+PA的最小值;(3)、是否存在点P,使其在运动过程中满足△EQP △EBC,若存在,求出点P坐标;若不存在,请说明理由.27. 如图,直线y=2x-1与x轴、y轴分别交于B、C两点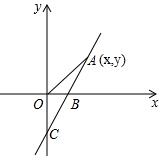 (1)、求点B的坐标;(2)、点A(x,y)是直线y= 2x-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、探究:①当点A的坐标是多少时,△AOB的面积为 ,并说明理由;
(1)、求点B的坐标;(2)、点A(x,y)是直线y= 2x-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、探究:①当点A的坐标是多少时,△AOB的面积为 ,并说明理由;②在①成立的情况下,x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请写出满足条件的三个P点坐标即可;若不存在,请说明理由。
-