山西省忻州市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-13 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{2}$ 的相反数是（）

A、 $\frac{1}{\sqrt{2}}$ B、 $- \sqrt{2}$ C、 $- \frac{1}{\sqrt{2}}$ D、 $\sqrt{2}$

查看试题解析
2. 气象台为了预报台风，首先要确定台风中心的位置，则下列说法能确定台风中心位置的是（）

A、西太平洋 B、距电台500海里 C、北纬 $128 °$ ，东经 $36 °$ D、湛江附近

查看试题解析
3. 由 $\frac{x}{3} - \frac{y}{2} = 1$ 可以得到用 $x$ 表示 $y$ 的式子为（）

A、 $y = \frac{2 x - 2}{3}$ B、 $y = \frac{2 x}{3} - 2$ C、 $y = \frac{2 x}{3} - \frac{1}{3}$ D、 $y = 2 - \frac{2 x}{3}$

查看试题解析
4. 空气是多种气体的混合物．空气主要由氮气、氧气、稀有气体（氦、氖、氩、氪、氙、氡、气奥），二氧化碳以及其他物质（如水蒸气、杂质等）组合而成．为直观介绍空气各成分的百分比，最适合用的统计图是（）

A、折线图 B、条形图 C、直方图 D、扇形图

查看试题解析
5. 下列说法不正确的是（）

A、不等式 $x - 3 > 2$ 的解集是 $x > 5$ B、不等式 $x < 3$ 的整数解有无数个 C、不等式 $x + 3 < 3$ 的整数解是0 D、 $x = 0$ 是不等式 $2 x < 3$ 的一个解

查看试题解析
6. 某校七（3）班的同学进行了一次安全知识测试，测试成绩进行整理后分成四个组，并绘制如图所示的频数直方图，则第二组的频数是（）

A、0.4 B、18 C、0.6 D、27

查看试题解析
7. 如图， $∠ C D B$ 与 $∠ D B E$ 是同旁内角，它们是由（）

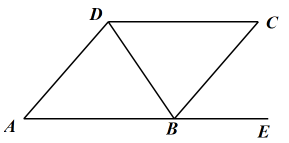A、直线 $C D$ ， $A B$ 被直线 $B D$ 所截形成的 B、直线 $A D$ ， $B C$ 被直线 $A E$ 所截形成的 C、直线 $D C$ ， $A B$ 被直线 $A D$ 所截形成的 D、直线 $D C$ ， $A B$ 被直线 $B C$ 所截形成的

查看试题解析
8. 老师：若实数 $a$ ， $b$ ， $c$ 在数轴上对应点的位置如图所示，学生1： $a c > b c$ ；学生2： $a + b > c + b$ ；学生3： $a + c > b + c$ ；学生4： $a b > c b$ ．老师：只有1名学生的结论是正确的．这名学生是（）

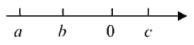A、学生1 B、学生2 C、学生3 D、学生4

查看试题解析
9. 给出下列命题中真命题的是（）

A、两条直线被第三条直线所截，同位角相等 B、平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交 C、从直线外一点到这条直线的垂线段，叫做该点到直线的距离 D、过一点作已知直线的平行线，有且只有一条

查看试题解析
10. “阅读与人文滋养内心”，重庆一中初二年级正掀起一股阅读《红星照耀中国》的浪潮.小明4天里阅读的总页数比小颖5天里阅读的总页数少100页，小颖平均每天阅读的页数比小明平均每天阅读的页数的2倍少10页.若小明、小颖平均每天分别阅读x页、y页，则下列方程组正确的是（）

A、 ${\begin{array}{l} 4 x - 100 = 5 y \\ y = 2 x - 10 \end{array}$ B、 ${\begin{array}{l} 4 x + 100 = 5 y \\ y = 2 x + 10 \end{array}$ C、 ${\begin{array}{l} 4 x = 5 y - 100 \\ y = 2 x - 10 \end{array}$ D、 ${\begin{array}{l} 4 x = 5 y + 100 \\ y = 2 x + 10 \end{array}$

查看试题解析

二、填空题

11. $\sqrt{4 × 25} =$ ．

查看试题解析
12. 在平面直角坐标系中，点 $P (1 ， - 1)$ 的纵坐标是．

查看试题解析
13. 我们知道，适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解．同样地，适合三元一次方程的一对未知数的值叫做这个三元一次方程的一个解．请写出方程 $x + y + z = 4$ 的一个正整数解．

查看试题解析
14. 小芸为了解同学们最感兴趣的在线学习方式，设计了如下的调查问题（选项不完整）：你最感兴趣的一种在线学习方式是（）（单选）
$A$ ． $B$ ． $C$ ． $D$ ．其他
她准备从“①在线听课，②在线讨论，③在线学习 $2 ~ 3$ 小时，④用手机在线学习，⑤在线阅读”中选取三个作为该问题的备选答案，合理的选取是．（填序号）

查看试题解析
15. 若不等式组 ${\begin{array}{l} x - a > 2 \\ b - 2 x > 0 \end{array}$ 的解集为 $- 1 < x < 1$ ，则a+b的立方根是．

查看试题解析
16. 公元前6世纪古希腊的毕达哥拉斯学派有一种观点，即“万物皆数”，一切量都可以用整数或整数比（分数）表示，后来，当这一学派中的希帕索斯发现，边长为1的正方形的对角线的长度不能用整数或整数的比表示，毕达哥拉斯学派感到惊恐不安，由此，引发了第一次数学危机，这里的“不能用整数或整数的比表示的数”指的是．

查看试题解析

三、解答题

17.

(1)、计算： $| \sqrt{2} - \sqrt{3} | - 2 \sqrt{3}$ ；

(2)、解不等式 ${\begin{array}{l} 3 (x - 1) + 1 > 5 x \\ 5 - (2 x - 1) < 4 x \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
18. 如图，已知 $∠ 4 = ∠ B$ ， $∠ 1 = ∠ 3$ ，求证：AC平分 $∠ B A D$ ．

查看试题解析

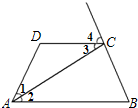19. 下面是小马虎解不等式

\frac{x - 3}{2} + 1 \geq \frac{2 x + 1}{3}

的过程如下，请认真阅读并完成相应任务：

去分母得 $3 (x - 3) + 6 ≥ 2 (2 x + 1)$ ． …………第一步

去括号得 $3 x - 9 + 6 ≥ 4 x + 2$ ． ………………第二步

移项得 $3 x - 4 x ≥ 2 + 9 + 6$ ． …………………第三步

合并同类项得 $- x ≥ 17$ ． ……………………第四步

系数化1得 $x ≤ - 17$ ． ………………………第五步

任务一：以上求解过程中，去分母的依据是；

第步开始出现错误，这一步不正确的原因是．

任务二：请直接写出该不等式的解集：；

任务三：请你根据平时的学习经验，就解不等式需要注意的事项给其他同学提一条建议．

查看试题解析

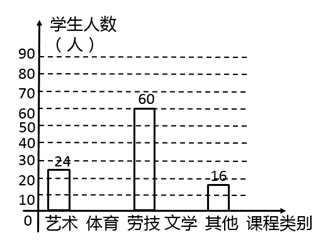
20. 《中共中央国务院关于深化教育教学改革全面提高义务教育质量的意见》指出：坚持“五育”并举，全面发展素质教育，为深化义务教育课程改革，某中学校积极开展拓展性课程建设，计划开设艺术、体育、劳技、文学等多个类别的拓展性课程，要求每一位学生仅选择一个类别的拓展性课程，为了了解学生选择拓展性课程的情况，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图（部分信息未给出）：
某校选择拓展课程的人数条形统计图
某校选择拓展课程的人数扇形统计图
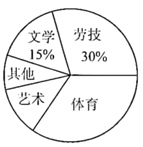
根据统计图中的信息，解答下列问题：

(1)、本次被调查的学生人数为；

(2)、将“体育”与“文学”对应的条形图补充完整；

(3)、扇形统计图中“体育”对应的圆心角为 $°$ ；

(4)、若该校共有1800名学生，请估计全校选择体育类的学生人数．

查看试题解析
21. 七年级张老师给了学生小强21元钱买笔和笔记本，已知每支笔3元，每本笔记本2.2元，他买了3支笔，请你帮他算一算，他最多还可以买几本笔记本？

查看试题解析
22. 先阅读下面材料，再完成任务：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：
已知实数 $x$ ， $y$ 满足 $3 x - y = 5$ ， ……①， $2 x + 3 y = 7$ ， ……②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值．
本题常规思路是将①②两式联立组成方程组，解得 $x$ ， $y$ 的值再代入欲求值的代数式得到答案，常规思路运算量比较大．其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由①－②可得 $x - 4 y = - 2$ ，由①＋②×2可得 $7 x + 5 y = 19$ ，这样的解题思想就是通常所说的“整体思想”
解决问题：

(1)、已知二元一次方程组 ${\begin{array}{l} 3 x - 2 y = - 2 \\ 2 x - 3 y = - 3 \end{array}$ ，则 $x - y =$ ， $x + y =$ ；

(2)、某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记木共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？

(3)、对于实数 $x$ ， $y$ ，定义新运算： $x * y = a x + b y + c$ ，其中 $a$ ， $b$ ， $c$ 是常数，等式右边是通常的加法和乘法运算．已知 $3 * 5 = 15$ ， $4 * 7 = 28$ ，那么 $1 * 1 =$ ．

查看试题解析
23. 综合与实践，某校为严格落实《教育部办公厅关于做好学校疫情防控后勤工作的通知》（教电[2020]88号）的文件要求和学校下发的做好疫情防控工作的通知，保障全校师生身体健康和生命安全积极应对校园的疫情防控工作，后勤处与医疗器械供应商联系及时购买质量合格、数量充足的防护物资，如消杀药品和医用外科口罩，医用防护服、体温计、护目镜等防护用品，计划购买 $A$ ， $B$ 两种型号的测温仪，计划购买 $A$ ， $B$ 两种型号的测温仪，已知购买5个 $A$ 型测温仪和3个 $B$ 型测温仪共需1480元，购买3个 $A$ 型测温仪和4个 $B$ 型测温仪共需1240元．

(1)、每个 $A$ 型测温仪和每个 $B$ 型测温仪的价格分别是多少元？

(2)、学校计划购买 $A$ ， $B$ 两种型号的测温仪共30个，并且总费用不超过5280元， $A$ 型的测温仪最多能购买多少个？

查看试题解析
24. 如图，在平面直角坐标系中，点 $A$ ， $B$ 的坐标分别为 $(- 1 ， 0)$ ， $(3 ， 0)$ ，现同时将 $A$ ， $B$ 两点先向上平移2个单位长度，再向右平移1个单位长度，分别得到点 $A$ ， $B$ 的对应点 $D$ ， $C$ ，连接 $A D$ ， $B C$ ， $C D$ ．

(1)、写出点 $D$ ， $C$ 的坐标分别是，；四边形 $A B C D$ 的面积为；

(2)、在 $x$ 轴上是否存在点 $P$ ，连接 $C P$ ， $D P$ ，使得三角形 $P C D$ 面积是三角形面积 $P B C$ 的2倍，若存在，请求出点 $P$ 的坐标：若不存在，请说明理由；

(3)、若点 $Q$ 是直线 $B C$ 上一点，连接 $Q A$ ， $Q D$ ，请你直接写出 $∠ A Q D$ ， $∠ Q D C$ 与 $∠ Q A B$ 的数量关系．

查看试题解析