山西省临汾市襄汾县2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-13 类型：期末考试

进入出卷网下载

一、单选题

1. 下列防疫的图标中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，Rt△ABC沿直角边BC所在直线向右平移到Rt△DEF，则下列结论中，不正确的是（）

A、 $B E = E C$ B、 $B C = E F$ C、 $A C = D F$ D、 $△ A B C ≌ △ D E F$

查看试题解析
3. 下列说法正确的是（）

A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、面积相等的两个三角形全等 D、全等三角形的面积一定相等

查看试题解析
4. 已知 $a < b$ ，则下列四个不等式中，不正确的是（）

A、 $2 a < 2 b$ B、 $- 5 a < - 5 b$ C、 $a - 2 < b - 2$ D、 $1.2 + a < 1.2 + b$

查看试题解析
5. 《九章算术》是我国东汉年间编订的一部数学经典著作，其中有一个问题是：今有三人公车，二车空；二人公车，九人步．问：人与车各几何？其大意如下：有若干人要坐车，若每3人坐一辆车，则有2辆空车；若每2人坐一辆车，则有9人需要步行，问人与车各多少？设共有x人，y辆车，则可列方程组为（）

A、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y + 9 = x \end{array}$ B、 ${\begin{array}{l} 3 y - 2 = x \\ 2 y + 9 = x \end{array}$ C、 ${\begin{array}{l} 3 y - 2 = x \\ 2 (y + 9) = x \end{array}$ D、 ${\begin{array}{l} 3 (y - 2) = x \\ 2 y - 9 = x \end{array}$

查看试题解析
6. 如图， $Δ A B C$ 中 $∠ B A C = 100 °$ ，将 $Δ A B C$ 绕点 $A$ 逆时针旋转 $150 °$ ，得到 $Δ A D E$ ，这时点B、C、D恰好在同一直线上，则 $∠ E$ 的度数为（）

A、 $50^{\circ}$ B、 $75^{\circ}$ C、 $65^{\circ}$ D、 $60^{\circ}$

查看试题解析
7. 若关于x的方程2x+2＝m﹣x的解为负数，则m的取值范围是（）

A、m＞2 B、m＜2 C、m＞ $\frac{2}{3}$ D、m＜ $\frac{2}{3}$

查看试题解析
8. 如图，△ABC与△A′B′C′关于点O成中心对称，则下列结论不成立的是（）

A、点A与点A′是对称点 B、BO＝B′O C、AB∥A′B′ D、∠ACB＝∠C′A′B′

查看试题解析
9. 如图，正五边形ABCDE，BG平分∠ABC，DG平分正五边形的外角∠EDF，则∠G＝（）

A、36° B、54° C、60° D、72°

查看试题解析
10. 如图，长方形 ABCD 中，AB＝6，第一次平移长方形 ABCD 沿 AB 的方向向右平移 5 个单位长度，得到长方形，第2次平移长方形沿 $A_{1} B_{1}$ 的方向向右平移 5个单位长度，得到长方形 $A_{2} B_{2} C_{2} D_{2}$ ， …，第n 次平移长方形 $A_{n - 1} B_{n - 1} C_{n - 1} D_{n - 1}$ 沿 $A_{n - 1} B_{n - 1}$ 的方向向右平移 5 个单位长度，得到长方形 $A_{n} B_{n} C_{n} D_{n}$ （n＞2），若 $A B_{n}$ 的长度为 2026，则 n 的值为（）

A、407 B、406 C、405 D、404

查看试题解析

二、填空题

11. 若 $(m + 1) x^{| m |} - 2 = 0$ 是关于x的一元一次方程，则m= ．

查看试题解析
12. 双塔寺又名永祚寺，创建于明万历三十六年（公元1608年），现为国家级文物保护单位，由于寺内双塔高耸，故俗称双塔寺，成为太原市的标志性建筑．主塔平面呈八角，其俯视图形状为正八边形（如图所示），则该八边形一个内角的度数为．

查看试题解析
13. 如图，在△ABC中，将△ABC沿直线m翻折，点B落在点D的位置，若∠1−∠2=60°，则∠B的度数是．

查看试题解析
14. 关于x的不等式组 ${\begin{array}{l} 2 x + 1 > 3 \\ a - x > 1 \end{array}$ 的解集为1＜x＜3，则a的值为．

查看试题解析
15. 如图，将长为 $5 c m$ ，宽为 $3 c m$ 的长方形 $A B C D$ 先向右平移 $2 c m$ ，再向下平移 $1 c m$ ，得到长方形 $A^{'} B^{'} C^{'} D^{'}$ ，则阴影部分的面积为 $c m^{2}$ ．

查看试题解析

三、解答题

16. 解下列方程与方程组：

(1)、解方程： $\frac{x - 3}{2} - \frac{2 x - 5}{3} = 1$

(2)、解方程组： ${\begin{array}{l} x - y = 2 \\ x - 2 y = - 3 \end{array}$

查看试题解析
17. 解不等式 $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} \geq 1$ ，并把它的解集在数轴上表示出来．

查看试题解析
18. 如图，在8×8的方格纸中有两条直线m，n和△ABC，其中直线m⊥n于点O．请按要求解答．

(1)、将△ABC向右平移4个单位，在图①中画出平移后的△A₁B₁C₁；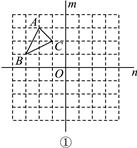

(2)、在图②中画出△ABC关于直线n对称的△A₂B₂C₂；

(3)、将△ABC绕原点O旋转180°，在图③中画出旋转后的△A₃B₃C₃ ．

查看试题解析
19. 解方程组 ${\begin{array}{l} x - 3 y = 8 ① \\ 4 x - 3 y = 5 ② \end{array}$ 时，两位同学的解法如下：
解法一：由① $-$ ②，得 $3 x = 3$
解法二：由②得 $3 x + (x - 3 y) = 5$ ③
把①代入③得 $3 x + 8 = 5$

(1)、反思：上述两种解题过程中你发现解法的解题过程有错误（填“一”或“二”），解二元一次方程组的基本思想．

(2)、请选择一种你喜欢的方法解此方程组．

查看试题解析
20. 如图，将三角形ABC绕点C顺时针旋转90°得到三角形EDC．若点A，D，E在同一条直线上，∠ACB＝20°，求∠ADC的度数．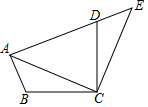

查看试题解析
21. 2020年受新冠疫情影响，全国中小学延迟开学，很多学校都开展起了线上教学，市场上对手写板的需求激增．重庆某厂家准备3月份紧急生产A，B两种型号的手写板，若生产20个A型号和30个B型号手写板，共需要投入36000元；若生产30个A型号和20个B型号手写板，共需要投入34000元．

(1)、请问生产A，B两种型号手写板，每个各需要投入多少元的成本？

(2)、若该厂家准备生产A，B两种型号的手写板共200个，总投入不高于14万元，请求出A型号手写板至少生产多少个．

查看试题解析
22. 综合与实践
如图，已知 $A B / / C D$ ，现将一直角三角形 $P M N$ 放入图中，其中 $∠ P = 90 °$ ， $P M$ 交 $A B$ 于点E， $P N$ 交 $C D$ 于点F．

(1)、当 $△ P M N$ 所放位置如图①所示时， $∠ P F D$ 与 $∠ A E M$ 的数量关系是；

(2)、当 $△ P M N$ 所放位置如图②所示时，求证： $∠ P F D - ∠ A E M = 90 °$ ；

(3)、在（2）的条件下，若 $M N$ 与 $C D$ 交于点O，且 $∠ D O N = 15 °$ ， $∠ P E B = 30 °$ ，求 $∠ N$ 的度数．

查看试题解析
23. 如图1，点D为 $Δ A B C$ 边BC的延长线上一点．

(1)、若 $∠ A ： ∠ A B C = 3 ： 4$ ， $∠ A C D = 140 °$ ，求 $∠ A$ 的度数；

(2)、若 $∠ A B C$ 的角平分线与 $∠ A C D$ 的角平分线交于点M，过点C作 $C P ⊥ B M$ 于点P．试说明： $∠ M C P = 90 ° - \frac{1}{2} ∠ A$ ；

(3)、在（2）的条件下，将 $Δ M C P$ 以直线BC为对称轴翻折可得到 $Δ N B C$ ， $∠ N B C$ 的角平分线与 $∠ N C B$ 的角平分线交于点Q（如图2），若 $∠ A = 60 °$ ，试求出 $∠ B Q C$ 的度数．

查看试题解析