河北省唐山市路北区2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-13 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、 B、 C、 D、2. 若a<b,则下列结论不一定成立的是( )A、 B、 C、 D、3. 为调查某大型企业员工对企业的满意程度,以下样本最具代表性的是( )
A、企业男员工 B、企业年满50岁及以上的员工 C、用企业人员名册,随机抽取三分之一的员工 D、企业新进员工4. 下列各点中,在第二象限的是( )A、(﹣1,3) B、(1,﹣3) C、(﹣1,﹣3 ) D、(1,3)5. 下列式子正确的是( )A、 B、 C、 D、6. 下列命题中,是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、直角的补角仍然是直角 D、垂线段最短7. 如图,AB∥CD,AF交CD于点E,∠A=45°,则∠CEF=( )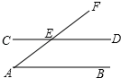 A、135° B、120° C、45° D、35°8. 解方程组的下列解法中,不正确的是( )A、代入法消去 , 由② 得 B、代入法消去 , 由① 得 C、加减法消去 , ①② 得 D、加减法消去 , ①② 得9. 不等式组 的解集在数轴上表示为( )A、
A、135° B、120° C、45° D、35°8. 解方程组的下列解法中,不正确的是( )A、代入法消去 , 由② 得 B、代入法消去 , 由① 得 C、加减法消去 , ①② 得 D、加减法消去 , ①② 得9. 不等式组 的解集在数轴上表示为( )A、 B、
B、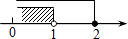 C、
C、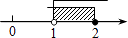 D、
D、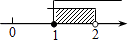 10. 估计 的值 ( )A、在3到4之间 B、在4到5之间 C、在5到6之间 D、在2到3之间11. 如图, , 点是上一点,且 , 若 , 则的度数为( )
10. 估计 的值 ( )A、在3到4之间 B、在4到5之间 C、在5到6之间 D、在2到3之间11. 如图, , 点是上一点,且 , 若 , 则的度数为( )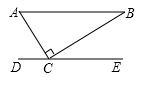 A、 B、 C、 D、12. 若关于x,y的方程组 的解满足 ,则m的最小整数解为( )A、﹣3 B、﹣2 C、﹣1 D、013. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )A、第一次向右拐40°,第二次向左拐140° B、第一次向左拐40°,第二次向右拐40° C、第一次向左拐40°,第二次向右拐140° D、第一次向右拐40°,第二次向右拐40°14. 数轴上表示1, 的对应点分别为A,B,点B关于点A的对称点为C,则点C所表示的数是( )
A、 B、 C、 D、12. 若关于x,y的方程组 的解满足 ,则m的最小整数解为( )A、﹣3 B、﹣2 C、﹣1 D、013. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是( )A、第一次向右拐40°,第二次向左拐140° B、第一次向左拐40°,第二次向右拐40° C、第一次向左拐40°,第二次向右拐140° D、第一次向右拐40°,第二次向右拐40°14. 数轴上表示1, 的对应点分别为A,B,点B关于点A的对称点为C,则点C所表示的数是( )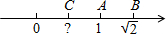 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
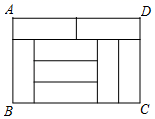
15. 用不等式表示“的2倍与3的和不大于2”为 .16. 如图,由 个大小相同的小长方形无缝拼接成一个大长方形,已知大长方形的周长为 ,则小长方形的周长为 .
 17. 一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,则第5组的频率为 .18. 某次数学测验,共16个选择题,评分标准为:答对一题给6分,答错一题扣2分,不答得0分.某个学生只有1题未答,他想自己的分数不低于70分,他至少要答对道题.
17. 一次数学测试后,某班40名学生按成绩分成5组,第1、2、3、4组的频数分别为13、10、6、7,则第5组的频率为 .18. 某次数学测验,共16个选择题,评分标准为:答对一题给6分,答错一题扣2分,不答得0分.某个学生只有1题未答,他想自己的分数不低于70分,他至少要答对道题.三、解答题
-
19. 计算:(1)、;(2)、 .20. 解方程组:21. 解不等式组 ,并把它的解集在数轴上表示出来.
 22. 三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(-1,4),B(-4,-1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1 .
22. 三角形ABC在平面直角坐标系中的位置如图所示,点O为坐标原点,A(-1,4),B(-4,-1),C(1,1).将三角形ABC向右平移3个单位长度,再向下平移2个单位长度得到三角形A1B1C1 .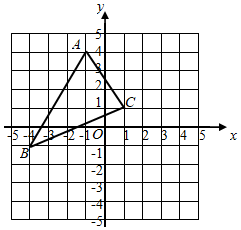 (1)、画出平移后的三角形;(2)、直接写出点A1 , B1 , C1的坐标:A1( ▲ , ▲ ),B1( ▲ ▲ ),C1( ▲ , ▲ );(3)、请直接写出三角形的面积为 .23. 为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:
(1)、画出平移后的三角形;(2)、直接写出点A1 , B1 , C1的坐标:A1( ▲ , ▲ ),B1( ▲ ▲ ),C1( ▲ , ▲ );(3)、请直接写出三角形的面积为 .23. 为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题: (1)、填空:样本容量为 , ;(2)、把频数分布直方图补充完整;(3)、求扇形B的圆心角度数;(4)、如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?24. 已知关于x,y的方程组 的解都为正数.(1)、求a的取值范围;(2)、已知 ,且 , ,求z的取值范围.25. 在综合与实践课上,老师让同学们以“两条平行线 , 和一块含角的直角三角尺”为主题开展数学活动.
(1)、填空:样本容量为 , ;(2)、把频数分布直方图补充完整;(3)、求扇形B的圆心角度数;(4)、如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?24. 已知关于x,y的方程组 的解都为正数.(1)、求a的取值范围;(2)、已知 ,且 , ,求z的取值范围.25. 在综合与实践课上,老师让同学们以“两条平行线 , 和一块含角的直角三角尺”为主题开展数学活动.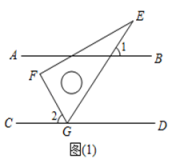
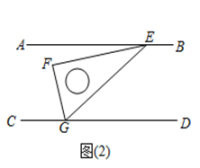 (1)、如图(1),若三角尺的角的顶点放在上,若 , 求的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点、分别放在和上,请你探索并说明与间的数量关系;26. 某电器超市销售每台进价分别200元,170元的 , 两种型号的电风扇,下表是近两周的销售情况:
(1)、如图(1),若三角尺的角的顶点放在上,若 , 求的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点、分别放在和上,请你探索并说明与间的数量关系;26. 某电器超市销售每台进价分别200元,170元的 , 两种型号的电风扇,下表是近两周的销售情况:销售时段
销售数量
销售收入
种型号
种型号
第一周
3台
5台
1800元
第二周
4台
10台
3100元
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)、求 , 两种型号的电风扇的销售单价;(2)、若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求 种型号的电风扇最多能采购多少台;(3)、在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.