河北省唐山市2020-2021学年七年级下学期期末数学试题

试卷更新日期：2022-04-13 类型：期末考试

进入出卷网下载

一、单选题

1. 如果 $m > n$ ，那么一定有 $- \frac{m}{2}$ □ $- \frac{n}{2}$ ， “□”中应填的符号是（）

A、 $>$ B、 $<$ C、 $\geq$ D、 $\leq$

查看试题解析
2. 如图，为估计池塘岸边 $A$ 、 $B$ 的距离，小方在池塘的一侧选取点 $O$ ，测得 $O A = 10$ 米， $O B = 8$ 米， $A$ 、 $B$ 间的距离不可能是（）

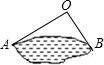A、20米 B、16米 C、14米 D、10米

查看试题解析
3. 若 $a$ 不为0，则 ${\underset{n}{\underset{︸}{(a \cdot a \cdot \cdot \cdot \cdot \cdot \cdot a)}}}^{2} =$ （）

A、 $a^{n + 2}$ B、 $2 a^{n}$ C、 $a^{n^{2}}$ D、 $a^{2 n}$

查看试题解析
4. 如图，在平面内经过一点作已知直线 $m$ 的平行线，可作平行线的条数有（）

A、0条 B、1条 C、0条或1条 D、无数条

查看试题解析
5. 下列式子从左到右变形是因式分解的是（）

A、12xy²＝3xy•4y B、（x+1）（x﹣3）＝x²﹣2x﹣3 C、x²﹣4x+1＝x（x﹣4）+1 D、x³﹣x＝x（x+1）（x﹣1）

查看试题解析
6. 对于等式 ${(a + b)}^{2} = a^{2} + b^{2}$ ，甲、乙、丙三人有不同看法，则下列说法符合题意是（）
甲：无论 $a$ 和 $b$ 取何值，等式均不能成立．
乙：只有当 $a = 0$ 时，等式才能成立．
丙：当 $a = 0$ 或 $b = 0$ 时，等式成立．

A、只有甲正确 B、只有乙正确 C、只有丙正确 D、三人说法均错误

查看试题解析
7. 如图， $B D$ 平分 $∠ A B C$ ，点 $E$ 为 $B A$ 上一点， $E G / / B C$ 交 $B D$ 于点 $F$ ．若 $∠ 1 = 35 °$ ，则 $∠ A E F$ 的度数为（）

A、70° B、35° C、25° D、17.5°

查看试题解析
8. 把不等式组 ${\begin{array}{l} x + 1 \geq 3 \\ - 2 x - 6 ＞ ﹣ 4 \end{array}$ 中每个不等式的解集在同一条数轴上表示出来，正确的为（）

A、 B、 C、 D、

查看试题解析
9. 如图，在 $△ A B C$ 中， $A D$ ， $A E$ 分别是边 $C B$ 上的中线和高， $A E = 6 c m$ ， $S_{△ A B D} = 12 c m^{2}$ ，则 $B C$ 的长是（）

A、 $4 c m$ B、 $6 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
10. 若 $a$ 是整数，则 $a^{2} + a$ 一定能被下列哪个数整除（）

A、2 B、3 C、5 D、7

查看试题解析

11. 定理：三角形的内角和等于180°．

已知： $△ A B C$ 的三个内角为 $∠ A$ 、 $∠ B$ 、 $∠ C$

求证： $∠ A + ∠ B + ∠ C = 180 °$ ．

证法1：如图

∵ $∠ A = 100 °$ ， $∠ B = 30 °$ ， $∠ C = 50 °$ （量角器测量）

∵ $100 ° + 30 ° + 50 ° = 180 °$ （计算所得）

∴ $∠ A + ∠ B + ∠ C = 180 °$ （等量代换）

证法2：如图，延长 $B C$ 到 $D$ ，过点 $C$ 作 $C E / / A B$ ．

∴ $∠ A = ∠ 2$ （两直线平行，内错角相等）

$∠ B = ∠ 3$ （两直线平行，同位角相等）

∵ $∠ 1 + ∠ 2 + ∠ 3 = 180 °$ （平角定义）．

∴ $∠ 1 + ∠ A + ∠ B = 180 °$ （等量代换）

即 $∠ A + ∠ B + ∠ C = 180 °$ ．

下列说法正确的是（）

A、证法1采用了从特殊到一般的方法证明了该定理 B、证法1还需要测量一百个进行验证，就能证明该定理 C、证法2还需证明其它形状的三角形，该定理的证明过程才完整 D、证法2用严谨的推理证明了该定理

查看试题解析

12. 若方程组 ${\begin{array}{l} 3 x + y = 1 - 3 a \\ x + 3 y = 1 + a \end{array}$ 的解满足 $x + y > - 2$ ，则 $a$ 的最大整数值是（）

A、-4 B、4 C、-2 D、2

查看试题解析
13. 如图， $△ A B C$ 中， $∠ A = 32 °$ ， $∠ B = 50 °$ ，将 $B C$ 边绕点 $C$ 按逆时针旋转一周回到原来位置，在旋转过程中，当 $C B^{'} / / A B$ 时，求 $B C$ 边旋转的角度，嘉嘉求出的答案是50°，琪琪求出的答案是230°，则下列说法正确的是（）

A、嘉嘉的结果正确 B、琪琪的结果正确正确 C、两个人的结果合在一起才符合题意 D、两个人的结果合在一起也错误

查看试题解析
14. 甲种细胞直径用科学记数法表示为 $8.05 \times 1 0^{- 6}$ ，乙种细胞直径用科学记数法表示为 $8.03 \times 1 0^{- 6}$ ，若甲、乙两种细胞直径的差用科学记数法表示为 $a \times 1 0^{n}$ ，则 $n$ 的值为（）

A、﹣5 B、﹣6 C、﹣7 D、﹣8

查看试题解析
15. 聪聪计算一道整式乘法的题： $(x + m) (5 x - 4)$ ，由于聪聪将第一个多项式中的“ $+ m$ ”抄成“ $- m$ ”，得到的结果为 $5 x^{2} - 34 x + 24$ ．这道题的符合题意结果是（）

A、 $5 x^{2} + 26 x - 24$ B、 $5 x^{2} - 26 x - 24$ C、 $5 x^{2} + 34 x - 24$ D、 $5 x^{2} - 34 x - 24$

查看试题解析
16. 已知关于x的不等式3x﹣m+1＞0的最小整数解为2，则实数m的取值范围是（）

A、4≤m＜7 B、4＜m＜7 C、4≤m≤7 D、4＜m≤7

查看试题解析

二、填空题

17. 二元一次方程组 ${\begin{array}{l} x + y = 10 \\ x - 2 y = 4 \end{array}$ 的解是．

查看试题解析
18. 分解因式：2ab³﹣2ab＝．

查看试题解析
19. 下图是某工人加工的一个机器零件（数据如图），经过测量不符合标准．标准要求是： $∠ E F D = 120 °$ ，且 $∠ A$ 、 $∠ B$ 、 $∠ C$ 保持不变为了达到标准，工人在保持 $∠ E$ 不变情况下，应将图中 $∠ D$ （填“增大”或“减小”）度．

查看试题解析

三、解答题

20.

(1)、计算： ${(- 2 x^{2})}^{3} + {(- 3 x^{2})}^{2} \cdot x^{2} + x^{8} \div x^{2}$

(2)、解不等式组： ${\begin{array}{l} 3 (x + 2) \geq 4 (x + 1) \\ x - \frac{x - 1}{3} > 1 \end{array}$ ，并把解集在图的数轴上表示出来．

查看试题解析
21.
画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．利用网格点和三角板画图或计算：

(1)、在给定方格纸中画出平移后的△A′B′C′；

(2)、画出AB边上的中线CD；

(3)、画出BC边上的高线AE；

(4)、△A′B′C′的面积为．

查看试题解析
22. 已知多项式 $A = {(x + 2)}^{2} + x (x - 2) - (x + 3) (x - 3)$

(1)、化简多项式 $A$ 时，小明的结果与其他同学的不同，请你检查小明同学的解题过程．

小明的作业：

解： $A = {(x + 2)}^{2} + x (x - 2) - (x + 3) (x - 3)$

$x^{2} \underline{+ 2 x} + 4 ① + x^{2} \underline{- 2 x} ② - x^{2} \underline{- 9} ③$

$= x^{2} - 5$

在标出①②③的几项中，出现不正确的是，请写出正确的解答过程；

(2)、小亮说：“只要给出 $x^{2} + 2 x + 1$ 的合理的值，即可求出多项式 $A$ 的值．”小明给出 $x^{2} + 2 x + 1$ 的值为4，请你求出此时 $A$ 的值．

查看试题解析
23. 如图， $∠ α$ 和 $∠ β$ 的度数满足方程组 ${\begin{array}{l} 2 ∠ α + ∠ β = 230 ° \\ 3 ∠ α - ∠ β = 20 ° \end{array}$ ，且 $C D / / E F$ ， $A C ⊥ A E$ ．

(1)、用解方程的方法求 $∠ α$ 和 $∠ β$ 的度数；

(2)、求 $∠ C$ 的度数．

查看试题解析
24. 某工程队计划招聘从事甲、乙两种工作的工人共150名，设从事甲工作的人数为 $x$ 人．

(1)、若招聘经理说：“招聘从事乙工作的人数是从事甲工作人数的2倍”．若设从事乙工作的人数为 $y$ 人，请列方程组解答从事甲、乙工作的人数各有多少人？

(2)、根据招聘工作人员透露：从事乙工作的人数比从事甲工作人数至少多25人，试通过列不等式的方法说明从事甲工作人数最多有多少人？

查看试题解析
25. 嘉琪在学习过程中，对教材的一个有趣的问题做如下探究：

(1)、【习题回顾】
已知：如图1，在 $△ A B C$ 中， $∠ A = 40 °$ ，角平分线 $B O$ 、 $C O$ 交于点 $O$ ．求 $∠ B O C$ 的度数【课本114页B组3题】
请直接写出 $∠ B O C =$ ；

(2)、【变式思考】
若 $∠ A = α$ ，请猜想 $∠ B O C$ 与 $α$ 的关系，并说明理由；

(3)、【拓展延伸】
已知：如图2，在 $△ A B C$ 中，角平分线 $B O$ 、 $C O$ 交于点 $O$ ， $O D ⊥ O B$ ，交边 $B C$ 于点 $D$ ，作 $∠ A B E$ 的平分线交 $C O$ 的延长线于点 $F$ ．若 $∠ F = β$ ，猜想 $∠ B A C$ 与 $β$ 的关系，并说明理由．

查看试题解析