河北省石家庄市辛集市2020-2021学年七年级下学期期末考试数学试题
试卷更新日期:2022-04-13 类型:期末考试
一、单选题
-
1. 北京2022年冬奥会会徽是以汉字“冬”为灵感来源设计的(如图).下面四个图案中,可以通过平移图案得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 9的平方根是( )A、3 B、±3 C、 D、±3. 在平面直角坐标系中,若点 在第三象限,则点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 方程组的解为 , 则被遮盖的两个数分别为( )A、9, B、9,1 C、7, D、5,15. 语句“的与的差不超过3”可以表示为( )A、 B、 C、 D、6. 不等式的解集在数轴上表示如下,正确的是( )A、
2. 9的平方根是( )A、3 B、±3 C、 D、±3. 在平面直角坐标系中,若点 在第三象限,则点 所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 方程组的解为 , 则被遮盖的两个数分别为( )A、9, B、9,1 C、7, D、5,15. 语句“的与的差不超过3”可以表示为( )A、 B、 C、 D、6. 不等式的解集在数轴上表示如下,正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
7. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( ) A、10° B、15° C、18° D、30°8. 如图,∠1和∠2不是同位角的是( )A、
A、10° B、15° C、18° D、30°8. 如图,∠1和∠2不是同位角的是( )A、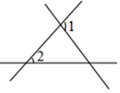 B、
B、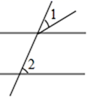 C、
C、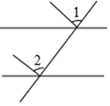 D、
D、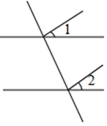 9. 如图,在平面直角坐标系中, 平行于 轴,点 坐标为 , 在 点的左侧, ,若 点在第二象限,则 的取值范围是( )
9. 如图,在平面直角坐标系中, 平行于 轴,点 坐标为 , 在 点的左侧, ,若 点在第二象限,则 的取值范围是( )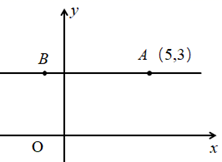 A、 B、 C、 D、10. 小聪、小明和小伶三位同学在同一所学校上学,该学校共有初一至高三6个年级,每个年级有6个班,每个班的人数在35~40之间.为了了解疫情期间所在学校学生的体育锻炼情况,他们各自设计了如下的调查方案:
A、 B、 C、 D、10. 小聪、小明和小伶三位同学在同一所学校上学,该学校共有初一至高三6个年级,每个年级有6个班,每个班的人数在35~40之间.为了了解疫情期间所在学校学生的体育锻炼情况,他们各自设计了如下的调查方案:小聪:我准备给全校每个班都发一份问卷,由体育委员代表班级填写完成.
小明:我准备把问卷发送到随机抽取的某个班的家长微信群里,通过网络提交完成.
小伶:我准备给每个班随机抽取3名同学各发一份问卷,填写完成.
则小聪、小明和小伶三人中,能较好地获得该校学生的体育锻炼情况的方案是( )
A、小聪 B、小明 C、小伶 D、小明和小伶11. 如果不等式组 有解,则 的取值范围是( ).A、 B、 C、 D、12. 在《九章算术》中记载一道这样的题:“今有甲、乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而亦钱五十,甲、乙持钱各几何?”题目大意是:甲、乙两人各带若干钱,如果甲得到乙所有钱的一半,那么甲共有钱50,如果乙得到甲所有钱的 ,那么乙也共有钱50.甲、乙两人各需带多少钱?设甲需带钱 ,乙带钱 ,根据题意可列方程组为A、 B、 C、 D、二、填空题
-
13. 若x-1有平方根,则实数的取值范围是 .14. 若点到两坐标轴的距离相等,则点的坐标是 .15. 把一张长方形纸片沿折叠后与的交点为 , 、分别在、的位置上,若 , 则 .
 16. 某小区一天收集各类垃圾共2.4吨,绘制成各类垃圾收集量的扇形图,其中湿垃圾在扇形图中对应的圆心角为135°,那么该小区这一天湿垃圾共收集了吨.17. 在长方形中,放入六个形状、大小相同的小长方形,所标尺寸如图所示.试求图中阴影部分的总面积为平方厘米.
16. 某小区一天收集各类垃圾共2.4吨,绘制成各类垃圾收集量的扇形图,其中湿垃圾在扇形图中对应的圆心角为135°,那么该小区这一天湿垃圾共收集了吨.17. 在长方形中,放入六个形状、大小相同的小长方形,所标尺寸如图所示.试求图中阴影部分的总面积为平方厘米. 18. 关于 , 的二元一次方程 , 无论取何值,所得到的方程都有一个相同解,则这个相同解是 .
18. 关于 , 的二元一次方程 , 无论取何值,所得到的方程都有一个相同解,则这个相同解是 .三、解答题
-
19.(1)、计算: .(2)、解方程组: .20. 解不等式组: , 并写出该不等式组的非负整数解.21. 已知△是由经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△
 (1)、观察表中各对应点坐标的变化,并填空:
(1)、观察表中各对应点坐标的变化,并填空:, , ;
(2)、在平面直角坐标系中画出及平移后的△;(3)、直接写出△的面积是 .22. 如图,平分 , F在上,G在上,与相交于点H, , 试说明 . (请通过填空完善下列推理过程)
解:∵(已知),( ▲ ).
∴ ▲ 180°(等量代换).
∴( ▲ ).
∴ ▲ ( ▲ ).
∵平分 ,
∴ ▲ ( ▲ ).
∴( ▲ ).
23. 我国数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根,华罗庚脱口说出答案,众人十分惊奇,忙问计算的奥妙.你知道他是怎样迅速准确地计算出结果的吗?下面是小超的探究过程,请补充完整:
(1)、求 ;①由103=1000,1003=1 000 000,可以确定 是位数;
②由59319的个位上的数是9,可以确定 的个位上的数是;
③如果划去59319后面的三位319得到数59,而33=27,43=64,可以确定 的十位上的数是;
由此求得 = .
(2)、已知103823也是一个整数的立方,用类似的方法可以求得 = .24. 中华文明,源远流长,中华汉字,寓意深广,为了传承优秀传统文化,某校九年级组织600名学生参加了一次“汉字听写”大赛.赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,97,100,73,76,80,77,81,86,89,82,85,71,68,74,98,90,97,100,84,87,73,65,92,96,60.
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩/分
频数
百分比
6
15%
8
20%

请根据所给信息,解答下列问题:
(1)、 , , , ;(2)、请补全频数分布直方图;(3)、若成绩在90分以上(包括90分)的为“优”等,请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人?25. 2020年12月7日,成都市郫都区新增1例本土新冠肺炎确诊病例,让全体市民再次加强了疫情防范意识.某单位准备用3000元购买医用口罩和洗手液发放给全体职工,若医用口罩购买500个,洗手液购买100瓶,则剩余200元;若医用口罩购买800个,洗手液购买80瓶,则还差40元.(1)、求医用口罩和洗手液的单价;(2)、根据疫情防控实际需要,单位决定购买医用口罩500个,洗手液和酒精消毒喷雾共90瓶,若需购买洗手液的瓶数最多为75瓶且购买酒精消毒喷雾的瓶数不超过洗手液瓶数的 , 酒精消毒喷雾每瓶的单价是32元,请你设计一种购买方案,要求所花的费用最少,并求出最少费用.26. 如图所示,、点在轴上,将三角形沿轴负方向平移,平移后的图形为三角形 , 且点的坐标为 . (1)、直接写出点的坐标;(2)、在四边形中,点从点出发,沿“”移动.若点的速度为每秒1个单位长度,运动时间为秒,回答下列问题:
(1)、直接写出点的坐标;(2)、在四边形中,点从点出发,沿“”移动.若点的速度为每秒1个单位长度,运动时间为秒,回答下列问题:①当 ▲ 秒时,点的横坐标与纵坐标互为相反数;
②求点在运动过程中的坐标(用含的式子表示,写出过程);
③当秒秒时,设 , , , 试问 , , 之间的数量关系能否确定?若能,请用含 , 的式子表示 , 写出方程;若不能,说明理由.