河北省保定市雄县2020-2021学年七年级下学期期末数学试题
试卷更新日期:2022-04-13 类型:期末考试
一、单选题
-
1. 在下列实数中,是无理数的是( )A、 B、 C、 D、3.142. 如图,若 , 则( )
 A、 B、 C、 D、3. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式4. 点A(-3,3)所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知a>b,下列不等式中不正确的是( )A、a+1>b+1 B、a﹣2>b﹣2 C、2a>2b D、﹣4a>﹣4b6. 今年我县有7000名学生参加中考,为了了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析.在这个问题中,下列说法正确的是( )A、这7000名考生的全体是总体 B、每个考生是个体 C、800名考生是总体的一个样本 D、样本容量是8007. 已知点在第一象限,则m的取值范围在数轴上表示正确的是( )A、
A、 B、 C、 D、3. 在下列四项调查中,方式正确的是A、了解本市中学生每天学习所用的时间,采用全面调查的方式 B、为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 C、了解某市每天的流动人口数,采用全面调查的方式 D、了解全市中学生的视力情况,采用抽样调查的方式4. 点A(-3,3)所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 已知a>b,下列不等式中不正确的是( )A、a+1>b+1 B、a﹣2>b﹣2 C、2a>2b D、﹣4a>﹣4b6. 今年我县有7000名学生参加中考,为了了解这些考生的数学成绩,从中抽取800名考生的数学成绩进行统计分析.在这个问题中,下列说法正确的是( )A、这7000名考生的全体是总体 B、每个考生是个体 C、800名考生是总体的一个样本 D、样本容量是8007. 已知点在第一象限,则m的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知 是方程 的一个解,那么 的值是( )A、-2 B、2 C、-4 D、49. 语句“x的与x的和不超过4”可以表示为( )A、 B、 C、 D、10. 把不等式组的解集表示在数轴上,正确的是( )A、
8. 已知 是方程 的一个解,那么 的值是( )A、-2 B、2 C、-4 D、49. 语句“x的与x的和不超过4”可以表示为( )A、 B、 C、 D、10. 把不等式组的解集表示在数轴上,正确的是( )A、 B、
B、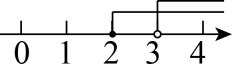 C、
C、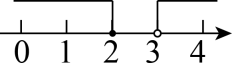 D、
D、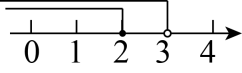 11. 在平面直角坐标系中,把点 先向左平移3个单位长度,再向上平移2个单位长度后得到的点的坐标是( )A、 B、 C、 D、12. 用加减法解方程组先消去y,需要用( )A、①×3+②×2 B、①×3-②×2 C、①×4+②×6 D、①+②13. 把一些书分给几名同学,若____;若每人分10本,则不够.依题意,设有x名同学,可列不等式 , 则横线上的信息可以是( )A、每人分7本,则可多分8个人 B、每人分7本,则剩余8本 C、每人分8本,则剩余7本 D、其中一个人分7本,则其他同学每人可分8本14. 下列命题中,真命题是( )A、4的平方根是2 B、同位角相等,两直线平行 C、同旁内角互补 D、0没有立方根15. 如果不等式(a-1)x>a-1的解集是x<1,那么a的取值范围是( )A、a≤1 B、a<1 C、a≥1 D、a<016. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、
11. 在平面直角坐标系中,把点 先向左平移3个单位长度,再向上平移2个单位长度后得到的点的坐标是( )A、 B、 C、 D、12. 用加减法解方程组先消去y,需要用( )A、①×3+②×2 B、①×3-②×2 C、①×4+②×6 D、①+②13. 把一些书分给几名同学,若____;若每人分10本,则不够.依题意,设有x名同学,可列不等式 , 则横线上的信息可以是( )A、每人分7本,则可多分8个人 B、每人分7本,则剩余8本 C、每人分8本,则剩余7本 D、其中一个人分7本,则其他同学每人可分8本14. 下列命题中,真命题是( )A、4的平方根是2 B、同位角相等,两直线平行 C、同旁内角互补 D、0没有立方根15. 如果不等式(a-1)x>a-1的解集是x<1,那么a的取值范围是( )A、a≤1 B、a<1 C、a≥1 D、a<016. 我国古代数学名著《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根木条,绳子还剩余4.5尺;将绳子对折再量木条,木条剩余1尺,问木条长多少尺?如果设木条长x尺,绳子长y尺,那么可列方程组为( )A、 B、 C、 D、二、填空题
-
17. 如下图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是 , 理由是 .
 18. 如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为度.
18. 如图,AB∥CD,BE交CD于点D,CE⊥BE于点E,若∠B=34°,则∠C的大小为度. 19. 已知实数a,b满足 . 则⑴当b=1时,a的值是;⑵若a,b均为正整数,当b取最大值时, .
19. 已知实数a,b满足 . 则⑴当b=1时,a的值是;⑵若a,b均为正整数,当b取最大值时, .三、解答题
-
20. 计算:(1)、(2)、21. 解不等式组 , 并把解集在数轴上表示出来.22. 如图 , 试说明 .
 23. 如图,是经过平移得到的,中任意一点平移后的对应点为 .
23. 如图,是经过平移得到的,中任意一点平移后的对应点为 . (1)、请写出平移的过程;(2)、分别写出点的坐标;(3)、画出平移后的图形;(4)、求出的面积24. 为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了200名学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(来完成),解答下列问题:
(1)、请写出平移的过程;(2)、分别写出点的坐标;(3)、画出平移后的图形;(4)、求出的面积24. 为了加强学生对新冠肺炎的预防意识,某校组织了学生参加新冠肺炎预防的知识竞赛,从中抽取了200名学生成绩(得分数取正整数,满分为100分)进行统计,绘制统计图如图(来完成),解答下列问题: (1)、a= , b=;(2)、扇形统计图中,D部分所对的圆心角为 , 求n的值并补全频数分布直方图;(3)、若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?25. 某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.(1)、求出该品牌应急灯、手电筒的定价分别是多少元?(2)、经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?26. 如图,在平面直角坐标系中,点 , 为轴负半轴上一点,点为轴正半轴上一点,其中满足方程 .
(1)、a= , b=;(2)、扇形统计图中,D部分所对的圆心角为 , 求n的值并补全频数分布直方图;(3)、若成绩在80分以上(不包括80分)优秀,全校共有1200名学生,估计成绩优秀的学生有多少名?25. 某公司保安部去商店购买同一品牌的应急灯和手电筒,查看定价后发现,购买一个应急灯和5个手电筒共需50元,购买3个应急灯和2个手电筒共需85元.(1)、求出该品牌应急灯、手电筒的定价分别是多少元?(2)、经商谈,商店给予该公司购买一个该品牌应急灯赠送一个该品牌手电筒的优惠,如果该公司需要手电筒的个数是应急灯个数的2倍还多8个,且该公司购买应急灯和手电筒的总费用不超过670元,那么该公司最多可购买多少个该品牌应急灯?26. 如图,在平面直角坐标系中,点 , 为轴负半轴上一点,点为轴正半轴上一点,其中满足方程 . (1)、求点、的坐标;(2)、点为轴负半轴上一点,且的面积为 , 求点的坐标;(3)、在上是否存在一点 , 使的面积等于的面积的一半,若存在,求出相应的点的坐标,若不存在,请说明理由.
(1)、求点、的坐标;(2)、点为轴负半轴上一点,且的面积为 , 求点的坐标;(3)、在上是否存在一点 , 使的面积等于的面积的一半,若存在,求出相应的点的坐标,若不存在,请说明理由.