河北省保定市安新县2020-2021学年七年级下学期期末考试数学试题

试卷更新日期：2022-04-13 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣8的立方根是（）

A、﹣4 B、﹣2 C、4 D、2

查看试题解析
2. 如图所示的网格中各有不同的图案，不能通过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 点A（﹣5，m²+1）在第几象限（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 一组数据中的最小值是33，最大值是103，若取组距为9．则组数为（）

A、7 B、8 C、9 D、7或8均可

查看试题解析
5. 木工师傅用图中的角尺画平行线，他依据的数学道理是（）

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、同旁内角互补，两直线平行 D、以上结论都不符合题意

查看试题解析
6. 如图，OE⊥AB，直线CD经过点O，∠COA＝35°，则∠BOD的余角度数为（）

A、35° B、45° C、55° D、60°

查看试题解析
7. 已知 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ 是关于 $x$ 、 $y$ 的二元一次方程 $x + m y = 5$ 的一组解，则 $m$ 的值是（）

A、1 B、-1 C、-2 D、2

查看试题解析
8. 把一副直角三角尺按如图方式摆放，点 $C$ 与点 $E$ 重合， $B C$ 边与 $E F$ 边都在直线 $l$ 上，若直线 $M N / / A C$ ，且 $M N$ 经过点 $D$ ，则 $∠ C D N =$ （）

A、 $30 °$ B、 $45 °$ C、 $65 °$ D、 $75 °$

查看试题解析
9. 图1是某手机店今年1～4月份手机销售总额的统计图，图2是今年该手机店某手机销售额占当月手机销售总额的百分比统计图．有以下四个结论，其中正确的为（）

A、今年该店4月份该手机销售额为65万元 B、今年该店4月份该手机销售额比3月份有所上升 C、今年该店4月份该手机销售额比3月份有所下降 D、今年该店3月份与4月份的该手机销售额无法比较，只能比较销售总额

查看试题解析
10. 如图，下列推理正确的是（）

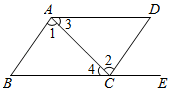A、∵AB∥CD，∴∠B＝∠DCE（两直线平行，同位角相等） B、∵∠1＝∠2，∴AD∥BC（内错角相等，两直线平行） C、∵AD∥BC，∴∠3＝∠4（内错角相等，两直线平行） D、∵∠B+∠BCD＝180°，∴AD∥BC（同旁内角互补，两直线平行）

查看试题解析
11. 如图，已知点A（2，﹣1），B（5，3），经过点A的直线l∥y轴，点C是直线l上一点，则当线段BC的长度最小时点C的坐标为（）

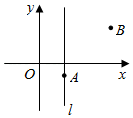A、（﹣1，3） B、（1，2） C、（3，2） D、（2，3）

查看试题解析
12. 如图，长方形内有两个相邻的正方形，面积分别为2和4，则阴影部分的面积为（）

A、 $2 \sqrt{2} - 2$ B、 $2 \sqrt{2} + 2$ C、2 D、 $1 + \sqrt{2}$

查看试题解析
13. 已知关于 $x$ ， $y$ 的二元一次方程 $2 x - 3 y = t$ ，其取值如下表，则 $p$ 的值为（）

$x$

$m$

$m + 2$

$y$

$n$

$n - 3$

$t$

5

$p$

A、16 B、17 C、18 D、19

查看试题解析
14. 甲商贩从一个农贸市场买西瓜，他上午买了30千克，价格为每千克a元，下午他又买了20千克价格为每千克b元后来他以每千克 $\frac{a + b}{2}$ 元的价格把西瓜全部卖给了乙，结果发现赔了钱，这是因为（）

A、a＜b B、a＞b C、a≥b D、a≤b

查看试题解析
15. 如图①，一张四边形纸片ABCD ， ∠A＝50°，∠C＝150°．若将其按照图②所示方式折叠后，恰好MD′∥AB ， ND′∥BC ，则∠D的度数为（）．

A、70° B、75° C、80° D、85°

查看试题解析
16. 在平面直角坐标系中，点A（0，a），点B（0，4﹣a），且A在B的下方，点C（1，2），连接AC，BC，若在AB，BC，AC所围成区域内（含边界），横坐标和纵坐标都为整数的点的个数为4个，那么a的取值范围为（）

A、﹣1 $<$ a $\leq$ 0 B、0 $<$ a $\leq$ 1 C、1 $\leq$ a $<$ 2 D、﹣1 $\leq$ a $\leq$ 1

查看试题解析

二、填空题

17. 若x＜y，且（m﹣2）x＞（m﹣2）y，则m的取值范围是．

查看试题解析
18. 已知点A（m﹣1，2m）在y轴上，则点A的坐标为．

查看试题解析
19. 我们用[m]表示不大于m的最大整数，如：[2]＝2，[4.1]＝4，[3.99]＝3．

(1)、[ $\sqrt{2}$ ]＝；

(2)、若[ $\sqrt{x}$ ]＝2，则x的取值范围是；

(3)、若[3+ $\sqrt{x}$ ]＝6，则x的取值范围是．

查看试题解析

三、解答题

20. 解不等式组 ${\begin{array}{l} 2 x + 1 > - (x + 5) ① \\ 2 (x + 1) - 6 \leq x ② \end{array}$ ．
请结合题意，完成本题的解答：

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
21. 请补全证明过程及推理依据．
已知：如图，点D，E，F分别是三角形ABC的边AB，AC，BC上的点，AB∥EF，∠DEF＝∠B．
求证：∠AED＝∠C．
证明：∵AB∥EF，
∴            ▲            ＝∠EFC（            ▲             ．
∵∠DEF＝∠B，
∴∠DEF＝∠EFC（            ▲            ）．
∴            ▲             （            ▲            ）．
∴∠AED＝∠C．

查看试题解析
22.

(1)、计算： $\sqrt{25} - \sqrt{5} \times | 2 - \sqrt{5} | - \sqrt[3]{- 1}$ ；

(2)、解方程组： ${\begin{array}{l} 2 x + 5 y = - 14 \\ \frac{1}{2} x - \frac{1}{3} y = \frac{5}{4} \end{array}$ ．

查看试题解析
23. 在大课间活动中，同学们积极参加体育锻炼．小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试，并以测试数据为样本分别绘制成如图1、图2所示的不完整的频数分布直方图（从左到右依次为第一小组到第六小组，每小组含最小值，不含最大值）和扇形统计图．
根据图中提供的信息，完成下列问题．

(1)、本次抽样调查的样本容量为；

(2)、将图1补充完整；

(3)、求第五小组对应圆心角的度数；

(4)、若“一分钟跳绳”次数不低于130次的成绩为优秀，全校共有1200名学生，根据图中提供的信息，估计该校“一分钟跳绳”成绩优秀的人数．

查看试题解析
24. 为了更好的治理西流湖水质，保护环境，市治污公司决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格，月处理污水量如下表：

A型

B型

价格（万元/台）

a

b

处理污水量（吨／月）

240

200

经调查：购买一台A型设备比购买一台B型设备多2万元，购买2台A型设备比购买3台B型设备少6万元．

(1)、求a，b的值；

(2)、经预算：市治污公司购买污水处理设备的资金不超过105万元，你认为该公司有哪几种购买方案；

(3)、在（2）问的条件下，若每月要求处理西流湖的污水量不低于2040吨，为了节约资金，请你为治污公司设计一种最省钱的购买方案．

查看试题解析
25. 如图1，直线 $A B$ 与 $C D$ 交于点 $F$ ，锐角 $∠ C D E = α$ ， $∠ A F C + α = 180 °$ ．

(1)、求证： $A B / / D E$ ；

(2)、若 $G$ 为直线 $A B$ 上一点（不与点 $F$ 重合）， $∠ F D G$ 的平分线与 $∠ D G B$ 的平分线所在的直线交于点 $P$ ．
①如图2， $α = 50 °$ ， $G$ 为射线 $F B$ 上一点，请补全图形并求 $∠ D P G$ 的度数；
② $∠ D P G$ 的度数为 ▲ （用含 $α$ 的式子表示）．

查看试题解析
26. 如图，平面直角坐标系中，已知点 $A (a ， 0)$ ， $B (0 ， b)$ ，其中 $a$ ， $b$ 满足 $\sqrt{a - b - 23} + | 2 a - 3 b - 39 | = 0$ ．将点 $B$ 向右平移24个单位长度得到点 $C$ ．点 $D$ ， $E$ 分别为线段 $B C$ ， $O A$ 上一动点，点 $D$ 从点 $C$ 以2个单位长度/秒的速度向点 $B$ 运动，同时点 $E$ 从点 $O$ 以3个单位长度/秒的速度向点 $A$ 运动，在 $D$ ， $E$ 运动的过程中， $D E$ 交四边形 $B O A C$ 的对角线 $O C$ 于点 $F$ ．设运动的时间为 $t$ 秒 $(0 < t < 10)$ ，四边形 $B O E D$ 的面积记为 $S_{四边形 B O E D}$ （以下面积的表示方式相同）．

(1)、求点 $A$ 和点 $C$ 的坐标；

(2)、若 $S_{四边形 E O E D} ≥ S_{四边形 A C D E}$ ，求 $t$ 的取值范围；

(3)、求证：在 $D$ ， $E$ 运动的过程中， $S_{Δ O E F} > S_{Δ D C F}$ 总成立．

查看试题解析

	A型	B型
价格（万元/台）	a	b
处理污水量（吨／月）	240	200

$x$	$m$	$m + 2$
$y$	$n$	$n - 3$
$t$	5	$p$