四川省凉山州2021年中考数学适应性试卷

试卷更新日期：2022-04-13 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、x²+ $\frac{1}{x^{2}}$ ＝1 B、ax²+bx+c＝0（a，b，c均为常数） C、（2x﹣1）（3x+2）＝5 D、（2x+1）²＝4x²﹣3

查看试题解析
2. 下图是用来证明勾股定理的图案被称为“赵爽弦图”，由四个全等的直角三角形和一个小正方形拼成的大正方形，对其对称性表述，正确的是（）

A、轴对称图形 B、中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形又不是中心对称图形

查看试题解析
3. 关于二次函数y＝2x²﹣4x+3的图象，下列叙述正确的是（）

A、顶点坐标是（﹣1，1） B、对称轴是直线x＝1 C、当x>1时，y随x的增大而减小 D、该图象与x轴有两个交点

查看试题解析
4. 为响应政府号召，加强防疫物资储备，我州某服装厂改装一条生产线加工口罩，今年一月口罩产量是80万只，第一季度总产量是340万只，设二、三月份的产量月平均增长率为x，根据题意可得方程为（）

A、80(1+x)²＝340 B、80+80(1+x)+80(1+2x)＝340 C、80(1+x)³＝340 D、80+80(1+x)+80(1+x)²＝340

查看试题解析
5. 若事件“对于二次函数y=x²-2mx+1，当x<1时，y随x的增大而减小”是必然事件，则实数m的取值范围是（）

A、m≥1 B、m≤1 C、m>1 D、m<1

查看试题解析
6. 如图，Rt△OCB的斜边OB在y轴上，OC= $\sqrt{3}$ ， ∠BOC=30°，直角顶点C在第二象限，将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′，则B点的对应点B′的坐标和点B在旋转过程中绕过的路径长分别是（）

A、 $(\sqrt{3} ， - 1)$ 和 $\frac{4}{3} π$ B、 $(1 ， - \sqrt{3})$ 和 $\frac{2}{3} π$ C、(2，0)和 $\frac{4}{3} π$ D、 $(\sqrt{3} ， 0)$ 和 $\frac{2}{3} π$

查看试题解析
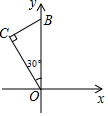7. 西昌市“北环线“是市政府为进一步优化市区交通布局打造的重点民生工程，如图，其中公路弯道处是一段圆弧 $\overset{⌢}{A B}$ ，点O是这条弧所在圆的圆心，点C是 $\overset{⌢}{A B}$ 的中点，OC与AB相交于点D.经测量AB=120m，CD=20m，那么这段弯道的半径为（）

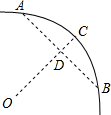A、100m B、90m C、100 $\sqrt{3}$ m D、90 $\sqrt{3}$ m

查看试题解析
8. 关于x的一元二次方程（k﹣2）x²﹣2kx+k﹣6＝0有两个实数根，则k的取值范围是（）

A、k≥0 B、k≥0且k≠2 C、k≥ $\frac{3}{2}$ D、k≥ $\frac{3}{2}$ 且k≠2

查看试题解析
9. 下列说法正确的是（）

A、平分弦的直径垂直于弦 B、圆的内接四边形的对角相等 C、三点确定一个圆 D、三角形的任意两边垂直平分线的交点是三角形的外心

查看试题解析
10. 一个圆锥的底面半径为1cm，侧面积为4πcm² ，现将其侧面展开平铺成的扇形的圆心角为（）

A、90° B、135° C、60° D、45°

查看试题解析
11. 如图，已知⊙O的半径是2，点A，B，C在⊙O上，若四边形OABC为菱形，则图中阴影部分面积为（）

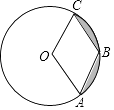A、 $\frac{2}{3}$ π﹣2 $\sqrt{3}$ B、 $\frac{1}{3}$ π﹣ $\sqrt{3}$ C、 $\frac{4}{3}$ π﹣2 $\sqrt{3}$ D、 $\frac{4}{3}$ π﹣ $\sqrt{3}$

查看试题解析
12. 抛物线y＝ax²+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴是x＝﹣ $\frac{1}{2}$ ，结合图象分析下列结论：①abc>0；②a+b+c>0；③a+b＝0；④2a+c>0；⑤一元二次方程ax²+bx+c＝0的两根分别为x₁＝﹣3，x₂＝2；⑥ $\frac{4 a c - b^{2}}{4 a}$ >0；⑦若两点（﹣2，y₁），（3，y₂）在二次函数图象上，则y₁>y₂；其中正确的结论有（）

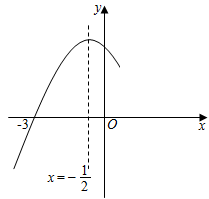A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

13. 将分别标有“学”“习”“强”“国”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其它差别，每次摸球前先搅拌均匀，随机摸出一球，不放回；再随机摸出一球，两次摸出的球上的汉字组成“强国”的概率是.

查看试题解析
14. 若y＝（m﹣1）x^|m^|+1+8mx﹣8是关于x的二次函数，则其图象与x轴的交点坐标为 .

查看试题解析
15. 将△ABC在平面内绕点A旋转40°到△AB'C'的位置，使CC'∥AB.则∠CAB'的度数为.

查看试题解析
16. 抛物线y＝﹣x²+bx+c的部分图象如图所示，其对称轴是x＝﹣1，若y≥3，则x的取值范围为．

查看试题解析
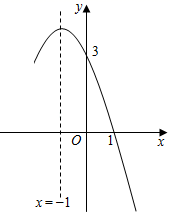17. 如图，PA、PB是⊙O的切线，切点分别为A、B，BC是⊙O的直径，PO交⊙O于E点，连接AB交PO于F，连接CE交AB于D点.下列结论：①PA＝PB；②OP⊥AB；③CE平分∠ACB；④OF＝ $\frac{1}{2}$ AC；⑤E是△PAB的内心；⑥△CDA≌△EDF.其中一定成立的是（只填序号） .

查看试题解析
18. 已知 $⊙ O$ 的半径 $O A = 1$ ，弦 $A B$ 、 $A C$ 的长分别是 $\sqrt{2}$ 、 $\sqrt{3}$ ，则 $∠ B A C$ 的度数是.

查看试题解析
19. 已知抛物线 $y = \frac{1}{4} x^{2} + 1$ 具有如下性质：该抛物线上任意一点到定点F(0，2)的距离与到 $x$ 轴的距离始终相等，如图，点M的坐标为 $(\sqrt{3} ， 3)$ ， P是抛物线 $y = \frac{1}{4} x^{2} + 1$ 上一个动点，则△PMF周长的最小值是.

查看试题解析

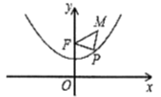
三、解答题

20. 解方程

(1)、2x²+3x﹣3＝0；

(2)、x（2x﹣5）＝10﹣4x.

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - (2 k + 4) x + k^{2} + 4 k + 3 = 0$ .

(1)、求证：不论k取何值，此一元二次方程总有两个不相等的实数根；

(2)、若此一元二次方程的两根是 $R t △ A B C$ 两直角边AB、AC的长，斜边BC的长为10，求k的值.

查看试题解析
22. 如图，在平面直角坐标系中， $R t Δ A B C$ 的三个顶点分别是 $A (- 3 ， 2)$ ， $B (0 ， 4)$ ， $C (0 ， 2)$ .

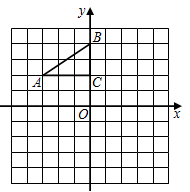(1)、将△ABC绕C点旋转180°，作出旋转后对应的△A₁B₁C₁；

(2)、平移△ABC到△A₂B₂C₂ ，使点A的对应点A₂的坐标为（﹣1，﹣4）；

(3)、若将△A₁B₁C₁绕某一点旋转可以得到△A₂B₂C₂ ，则该旋转中心的坐标为.

查看试题解析
23. 为了遏制新型冠状病毒疫情的蔓延势头，响应“停课不停学“的号召，某校决定为学生提供四类在线学习方式：在线阅读、在线听课、在线答疑、在线讨论，为了了解学生的需求，该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查(每位学生只能选择一种在线学习方式)，并根据调查结果绘制成两幅不完整的统计图.
请根据图中提供的信息，解答下列问题：

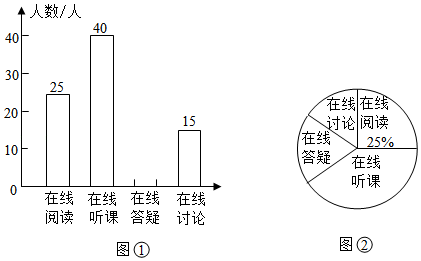(1)、本次调查的人数共有人；

(2)、请补全条形图，并求出“在线答疑”在扇形图中的圆心角度数为 ▲ ；

(3)、请用树状图或列举法求出甲乙两位学生选择同一种学习方式的概率.

查看试题解析
24. 如图，C是⊙O上一点，点P在直径AB的延长线上，PC是⊙O的切线，PB=2，PC=4.

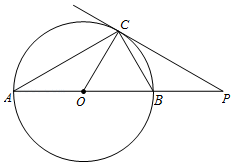(1)、求⊙O的半径长；

(2)、求∠BOC与∠BCP的数量关系，并说明理由.

查看试题解析
25. 为鼓励大学生毕业返乡创业拉动县域绿色特产销售，某县为大学生开设团队创业途径，某团队试销一款苦荞茶，成本为每千克30元，物价部门规定其销售单价不低于成本价且不高于成本价的2倍，经试销调研发现，销售过程中每天还要支付其他费用500元，日销售量y（千克）与销售单价x（元）符合一次函数关系，如图所示.

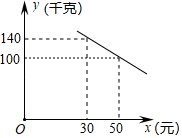(1)、求y与x之间的函数关系式，并根据题意写出自变量x的取值范围；

(2)、当每天的销售单价为多少时，该公司日获利最大？最大获利是多少元？

(3)、若在销售过程中每天的利润不低于700元，请确定销售单价的取值范围.

查看试题解析
26. 阅读下列材料：
平面上两点P₁（x₁ ， y₁），P₂（x₂ ， y₂）之间的距离表示为 $| P_{1} P_{2} | = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ ，称为平面内两点间的距离公式，根据该公式，如图，设P（x，y）是圆心坐标为C（a，b）、半径为r的圆上任意一点，则点P适合的条件可表示为 $\sqrt{{(x - a)}^{2} + {(y - b)}^{2}} = r$ ，变形可得：（x﹣a）²+（y﹣b）²＝r² ，我们称其为圆心为C（a，b），半径为r的圆的标准方程.例如：由圆的标准方程（x﹣1）²+（y﹣2）²＝25可得它的圆心为（1，2），半径为5.根据上述材料，结合你所学的知识，完成下列各题.

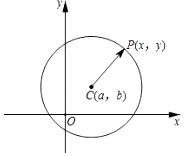(1)、圆心为C（3，4），半径为2的圆的标准方程为：_；

(2)、若已知⊙C的标准方程为：（x﹣2）²+y²＝2² ，圆心为C，请判断点A（3，﹣1）与⊙C的位置关系.

查看试题解析
27. 如图，在△ABC中，∠C＝90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆.

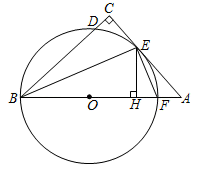(1)、求证：AC是⊙O的切线；

(2)、过点E作EH⊥AB，垂足为H，若CD＝1，EH＝3，求BE长.

查看试题解析
28. 如图1，在平面直角坐标系中，已知B点坐标为(1，0)，且OA=OC=3OB，抛物线y=ax²+bx+c(a≠0)图象经过A，B，C三点，其中D点是该抛物线的顶点.

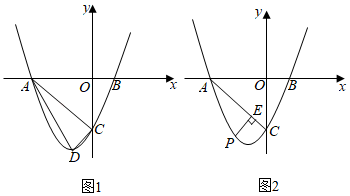(1)、求抛物线的解析式；

(2)、判断△ADC的形状并且求△ADC的面积；

(3)、如图2，点P是该抛物线第三象限部分上的一个动点，过P点作PE⊥AC于E点，当PE的值最大时，求此时P点的坐标及PE的最大值.

查看试题解析