广西壮族自治区玉林市玉州区2020-2021学年七年级下学期期中数学试卷
试卷更新日期:2022-04-13 类型:期中考试
一、单选题
-
1. 下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 点C在x轴的下方,y轴的右侧,距离x轴3个单位长度,距离y轴5个单位长度,则点C的坐标为( )
2. 点C在x轴的下方,y轴的右侧,距离x轴3个单位长度,距离y轴5个单位长度,则点C的坐标为( )
A、(-3,5) B、(3,-5) C、(5,-3) D、(-5,3)3. 下列四个图形中,能用 、 、 三种方法表示同一角的图形是( )A、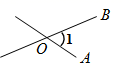 B、
B、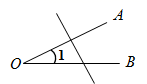 C、
C、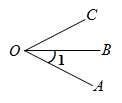 D、
D、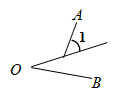 4. 下列说法错误的是( )A、﹣4是16的平方根 B、 的算术平方根是2 C、 的平方根是 D、 =55. 已知,点B在点的左侧,轴,且 , 则点B的坐标为( )A、 B、 C、 D、6. 下列四个命题中:
4. 下列说法错误的是( )A、﹣4是16的平方根 B、 的算术平方根是2 C、 的平方根是 D、 =55. 已知,点B在点的左侧,轴,且 , 则点B的坐标为( )A、 B、 C、 D、6. 下列四个命题中:①在同一平面内,互相垂直的两条直线一定相交
②有且只有一条直线垂直于已知直线
③两条直线被第三条直线所截,同位角相等
④从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离.
其中真命题的个数为( )
A、1个 B、2 个 C、3个 D、4个7. 若点P(m,1)在第二象限内,则点Q(1﹣m,﹣1)在( )A、x轴负半轴上 B、y轴负半轴上 C、第三象限 D、第四象限8. 若a是(﹣3)2的平方根,则 等于( )A、﹣3 B、 C、 或﹣ D、3或﹣39. 如图把一个长方形纸片,沿EF折叠后,点D,C分别落在D',C'的位置,若∠EFB= ,则∠AED'的度数为( ) A、30° B、53° C、40° D、45°10. 如图,直线l与∠BAC的两边分别相交于点D,E,则图中是同旁内角的有( )
A、30° B、53° C、40° D、45°10. 如图,直线l与∠BAC的两边分别相交于点D,E,则图中是同旁内角的有( ) A、2对 B、3对 C、4对 D、5对11. 定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )A、2 B、3 C、4 D、512. 下列命题中:
A、2对 B、3对 C、4对 D、5对11. 定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( )A、2 B、3 C、4 D、512. 下列命题中:①若 , 则点在原点处;
②点一定在第四象限
③已知点与点 , m,n均不为0,则直线平行x轴;
④已知点A(2,-3),轴,且 , 则B点的坐标为(2,2).
以上命题是真命题的有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
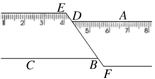
13. 在1, , , 0,这五个数中,最小的数是.14. 比较大小: 2(填“<”、“>”、或“=”).15. 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为 .
 16. 如图,在平面直角坐标系中,已知点 , , 连接 , 交y轴于B,且 , , 则点B坐标为.
16. 如图,在平面直角坐标系中,已知点 , , 连接 , 交y轴于B,且 , , 则点B坐标为. 17. 已知:如图,平分 , , , , 则.
17. 已知:如图,平分 , , , , 则. 18. 如图,将一副三角板按如图放置( , ),则下列结论:
18. 如图,将一副三角板按如图放置( , ),则下列结论:①;
②如果 , 则有;
③如果 , 则有;
④如果 , 必有.
其中正确的有(填序号).

三、解答题
-
19. 计算:.20. 求下列各式中的x .(1)、 x2﹣121=0(2)、(x﹣5)3+8=021. 已知2a﹣1的算术平方根是3,b﹣1是 的整数部分,c+1和9的平方根相等,求a﹣2b﹣c的值.22. 如图在平面直角坐标系中,的顶点坐标分别 , , .现将先向右平移6个单位长度,再向下平移5个单位长度,得到.
 (1)、直接写出点、、的坐标(2)、在平面直角坐标系中画出 , 并求出的面积.23. 阅读理解:因为 , 所以36的平方根为 , 即 , 所以36的算术平方根为6,即 ,(1)、计算: , ; , .
(1)、直接写出点、、的坐标(2)、在平面直角坐标系中画出 , 并求出的面积.23. 阅读理解:因为 , 所以36的平方根为 , 即 , 所以36的算术平方根为6,即 ,(1)、计算: , ; , .结论:;.(填“>”,“=”,“<”)
(2)、计算:①;②.
(3)、已知: , , 请用含a,b的式子表示.24. 结合图形填空:已知:如图, , .求证:.
证明:∵(已知),
又( ),
∴(等量代换),
∴( ),
∴(两直线平行,同旁内角互补).
又∵(已知),
∴( ),
∴(同旁内角互补,两直线平行),
∴( ).
25. 如图,已知点E、F在直线上,点G在线段上,与交于点H, , . (1)、求证:;(2)、试判断与之间的数量关系,并说明理由;(3)、若 , , 求的度数.(注:三角形内角和等于180°)26. 如图(1),在平面直角坐标系中,已知点 , , 且m,n满足 , 将线段向右平移2个单位长度,再向上平移4个单位长度,得到线段 , 其中点C与点A对应,点D与点B对应,连接 , .
(1)、求证:;(2)、试判断与之间的数量关系,并说明理由;(3)、若 , , 求的度数.(注:三角形内角和等于180°)26. 如图(1),在平面直角坐标系中,已知点 , , 且m,n满足 , 将线段向右平移2个单位长度,再向上平移4个单位长度,得到线段 , 其中点C与点A对应,点D与点B对应,连接 , .
 (1)、求点A、B、C、D的坐标;(2)、在x轴上是否存在点P,使三角形的面积等于平行四边形的面积?若存在,求出点P的坐标;若不存在,请说明理由;(3)、如图(2),点E在y轴的负半轴上,且.求证:.
(1)、求点A、B、C、D的坐标;(2)、在x轴上是否存在点P,使三角形的面积等于平行四边形的面积?若存在,求出点P的坐标;若不存在,请说明理由;(3)、如图(2),点E在y轴的负半轴上,且.求证:.