广西壮族自治区崇左市宁明县2020-2021学年七年级下学期期中数学试卷
试卷更新日期:2022-04-13 类型:期中考试
一、单选题
-
1. 64的平方根是( ).A、±8 B、±4 C、±2 D、±2. 下列几个数中,属于无理数的数是( )A、0.1 B、 C、π D、3. 下列各式中正确的是( )A、 B、 C、 D、4. 若 ,则实数 a 在数轴上对应的点的大致位置是( )A、
 B、
B、 C、
C、 D、
D、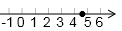 5. x与y的差的5倍与2的和是一个非负数,可表示为( )A、5(x-y)+2>0 B、5(x-y)+2≥0 C、x-5y+2≥0 D、5x-2y+2≤06. 若 , 下列不等式中错误的是( )A、 B、 C、 D、7. 一元一次不等式2x+1≥0的解集是( )A、x≥ B、x≤ C、x≥- D、x≤-8. 下列运算正确的是( )A、 B、 C、 D、9. 在数轴上表示不等式组 的解集,正确的是( )A、
5. x与y的差的5倍与2的和是一个非负数,可表示为( )A、5(x-y)+2>0 B、5(x-y)+2≥0 C、x-5y+2≥0 D、5x-2y+2≤06. 若 , 下列不等式中错误的是( )A、 B、 C、 D、7. 一元一次不等式2x+1≥0的解集是( )A、x≥ B、x≤ C、x≥- D、x≤-8. 下列运算正确的是( )A、 B、 C、 D、9. 在数轴上表示不等式组 的解集,正确的是( )A、 B、
B、 C、
C、 D、
D、 10. 计算结果为 的是( )A、 B、 C、 D、11. 某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折12. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形 , 把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )
10. 计算结果为 的是( )A、 B、 C、 D、11. 某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则至多可打( )A、6折 B、7折 C、8折 D、9折12. 如图,在边长为a的正方形中挖掉一个边长为b的小正方形 , 把余下的部分剪成一个矩形,通过计算两个图形(阴影部分)的面积,验证了一个等式是( )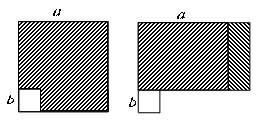 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 某种生物孢子的直径为0.00058m.把0.00058用科学记数法表示为 .14. 当y , 时,代数式 的值至少为1.15. 若不等式组 ,的解集是 ,则 的值为 .16. 计算: .17. 如果 是完全平方式,则 .18. 观察分析下列数据,按规律填空:、2、、2、、…、 (第n个数).
三、解答题
-
19. 计算:.20. 解不等式:1-≤+x21. 解不等式组. 把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.22. 计算:(1)、;(2)、.23. 先化简,再求值: , 其中 , .24. 观察下列算式:
①;
②;
③;
……
(1)、请按照以上规律写出第10个等式.(2)、请按照以上规律写出第n个等式(n为自然数,且n≥1).(3)、(2)中的式子一定成立吗?若不一定成立,请举出反例;若一定成立,请说出理由.25. 如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形. (1)、图②中的阴影部分的小正方形的边长等于.(2)、请用两种不同的方法列代数式表示图②中阴影部分的面积.(3)、观察图②,请写出 , , 这三个代数式之间的等量关系.(4)、根据(3)题中的等量关系,解决如下问题:若 , , 则求值.26. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买A、B两种型号的垃圾处理设备共10台.已知每台A型设备日处理能力为12吨;每台B型设备日处理能力为16吨.根据实际情况,要求B型设备不多于A型设备的3倍,且购回的设备日处理能力不低于142吨.请你为该景区设计购买A、B设备的方案.
(1)、图②中的阴影部分的小正方形的边长等于.(2)、请用两种不同的方法列代数式表示图②中阴影部分的面积.(3)、观察图②,请写出 , , 这三个代数式之间的等量关系.(4)、根据(3)题中的等量关系,解决如下问题:若 , , 则求值.26. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买A、B两种型号的垃圾处理设备共10台.已知每台A型设备日处理能力为12吨;每台B型设备日处理能力为16吨.根据实际情况,要求B型设备不多于A型设备的3倍,且购回的设备日处理能力不低于142吨.请你为该景区设计购买A、B设备的方案.