陕西省商洛市2022届高三下学期理数一模试卷

试卷更新日期：2022-04-12 类型：高考模拟

进入出卷网下载

一、单选题

1. 设复数z满足 $(1 - i) z = 2 \sqrt{2} i$ ，则|z|=（）

A、1 B、 $\sqrt{2}$ C、2 $\sqrt{2}$ D、2

查看试题解析
2. 设集合 $A = {- 1 ， - 2 ， - 3} ， B = {x | x^{2} + b x + 5 = 0}$ .若 $A ∩ B = {- 1}$ ，则B=（）

A、{-1，-3} B、{-1，3} C、 ${- 1 ， - 5}$ D、 ${- 1 ， 5}$

查看试题解析
3. 已知实数 $x ， y$ 满足约束条件 ${\begin{array}{l} y \leq 1 ， \\ x \leq 2 ， \\ x + 2 y - 1 \geq 0 ， \end{array}$ 则 $z = - x + y$ 的最大值为（）

A、-1 B、 $- \frac{5}{2}$ C、3 D、2

查看试题解析
4. “ $b > a + 1$ ”是 $3^{b} > 3^{a}$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 下图是国家统计局近期公布的全国居民消费价格的涨跌幅情况：
现有如下说法：
①2021年3月份，全国居民消费价格的同比和环比均呈现增长趋势②2021年1月至2022年1月，全国居民消费价格同比增长的月份有7个；③2021年1月至2022年1月中的任1个月，全国居民消费价格的环比呈现增长趋势的频率为 $\frac{1}{2}$ ④在2021年1月至2022年1月这个时段中，全国居民消费价格的同比与环比都增长的月份有5个
上述说法正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
6. $△ A B C$ 的内角A，B，C所对的边分别为a，b，c，已知 $B = \frac{π}{3} ， b c s i n A = 8 s i n B ， a = 2$ ，则b=（）

A、4 B、 $2 \sqrt{3}$ C、 $2 \sqrt{2}$ D、2

查看试题解析
7. 声音大小（单位： $d B$ ）取决于声波通过介质时所产生的压力（简称声压，单位： $N / m^{2}$ ）变化.已知声压x与声音大小y的关系式为 $y = 10 \times l g {(\frac{x}{2 \times 1 0^{- 5}})}^{2}$ .根据我国《工业企业噪声卫生标准》规定，新建企业工作地点噪音容许标准为85 $d B$ .若某新建企业运行时测得的声音大小为60 $d B$ ，符合《工业企业噪声卫生标准》规定，则此时声压为（）

A、2 $N / m^{2}$ B、20 $N / m^{2}$ C、0.2 $N / m^{2}$ D、0.02 $N / m^{2}$

查看试题解析
8. 已知直线 $x = \frac{π}{6}$ 是函数 $f (x) = s i n (ω x + \frac{π}{6}) （ 0 < ω < 8$ ）图象的一条对称轴，则f（x）的最小正周期为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{2}$ C、 $π$ D、2 $π$

查看试题解析
9. 如图所示的是某几何体的三视图，则该几何体的表面积为（）

A、60 B、54 C、48 D、24

查看试题解析
10. “杨辉三角”揭示了二项式系数在三角形中的一种几何排列规律，早在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中出现.如图，在由二项式系数所构成的“杨辉三角”中，若第n行中从左至右只有第12个数为该行中的最大值，则n=（）

A、21 B、22 C、23 D、24

查看试题解析
11. 若对任意的 $x \in (1 ， + \infty)$ ，恒有 $e^{a x} + \frac{1}{e^{a x}} \geq e^{l n x} + \frac{1}{e^{l n x}}$ ，则a的取值范围为（）

A、（—∞，e] B、 $(- ∞ ， - \frac{1}{e}] \cup [\frac{1}{e} ， + ∞)$ C、（—∞， $\frac{1}{e}$ ] D、[ $\frac{1}{e}$ ， +∞）

查看试题解析
12. 设 $F_{1}$ ， $F_{2}$ 分别为双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点，点A，B分别在双曲线C的左､右支上，若 $\vec{A B} = 5 \vec{F_{1} A} ， {\vec{A F_{2}}}^{2} = \vec{A B} \cdot \vec{A F_{2}}$ ，且 $| \vec{A F_{2}} | < | \vec{B F_{2}} |$ ，则双曲线C的渐近线斜率为（）

A、 $\pm \frac{6}{5}$ B、 $\pm \frac{4 \sqrt{5}}{5}$ C、 $\pm \frac{2 \sqrt{15}}{5}$ D、 $\pm \frac{4}{5}$

查看试题解析

二、填空题

13. 已知 $t a n (θ + \frac{5 π}{4}) = - 2$ ，则tanθ=.

查看试题解析
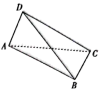
14. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} \cdot \vec{b} = - 4 ， \vec{a} \cdot (3 \vec{a} - \vec{b}) = 16$ ，则 $| \vec{a} | =$ .

查看试题解析
15. 已知抛物线 $C ： x^{2} = 2 p y (p > 0)$ 的焦点为F，点M在C上，且点M到点F的距离为13，到x轴的距离为9，则p=.

查看试题解析
16. 在 $△ A B C$ 中， $A B = A C = 2 ， c o s A = \frac{3}{4}$ ，将 $△ A B C$ 绕 $B C$ 旋转至 $△ B C D$ 的位置，使得 $A D = \sqrt{2}$ ，如图所示，则三棱锥 $D - A B C$ 外接球的表面积为.

查看试题解析

三、解答题

17. 已知正项等比数列{ $a_{n}$ }满足 $a_{1} = \frac{1}{2} ， a_{1} a_{5} = 4 (a_{3} - 1)$

(1)、求{ $a_{n}$ }的通项公式：

(2)、求数列{ $n + a_{n}$ }的前n项和 $S_{n}$ .

查看试题解析
18. 某地区实行社会主义新农村建设后，农村的经济收入明显增加.该地区为更好地了解农村的经济收入变化情况，对该地农村家庭年收入进行抽样调查，现将200户农村家庭2021年年收入的数据整理得到如下频率分布直方图；

(1)、估计该地区农村家庭年收入的平均值；（同一组中的数据用该组区间的中点值作代表）

(2)、用样本频率估计总体，现从该地区中随机抽取2户农村家庭，记家庭年均收入落在区间 $(9.5 ， 14.5]$ 内的户数为 $X$ ，家庭年均收入落在区间 $(7.5 ， 14.5]$ 内的户数为 $Y$ ，求E（X）与E（Y）的值.

查看试题解析
19. 在如图1所示的梯形ABCD中，已知 $A D / / B C ， A B ⊥ B C ， A D = \frac{1}{2} B C = 1$ ， E为BC的中点，将△DEC沿DE折起，得到如图2所示的四棱锥，且此时 $C_{1} - A B E D$ 的体积最大.

(1)、证明：平面 $A C_{1} D$ ⊥平面 $C_{1} E D$ .

(2)、若 $A C_{1} = \sqrt{6}$ ，求直线 $B C_{1}$ 与平面 $A C_{1} D$ 所成角的正弦值.

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左､右焦点分别为 $F_{1}$ （-c，0）， $F_{2}$ （c，0），点A（0，b）满足 $\vec{A F_{1}} \cdot \vec{A F_{2}} = 2 ， | \vec{A F_{1}} + \vec{A F_{2}} | = 2 \sqrt{3}$

(1)、求C的方程.

(2)、设过 $F_{2}$ 的直线 $l_{1}$ ， $l_{2}$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ，且 $k_{1} k_{2} = - 1$ ， $l_{1}$ 与C交于点D，E， $l_{2}$ 与C交于点G，H，线段DE与GH的中点分别为M，N.判断直线MN是否过定点.若过定点，求出该定点；若不过定点，请说明理由.

查看试题解析
21. 已知函数 $f (x) = \frac{e^{x}}{a} + (b - 1) x + 1$

(1)、当 $a = \frac{1}{4} ， b = - 1$ 时，求曲线 $y = f (x)$ 在点（0，f（0））处的切线方程；

(2)、当 $0 < a \leq e^{2}$ ，且 $x > 2$ 时， $f (x) > b l n [a (x - 1)$ ]恒成立，求b的取值范围.

查看试题解析
22. 在直角坐标系 $x O y$ 中，曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = 2 + 2 c o s θ \\ y = 2 s i n θ \end{array}$ （ $θ$ 为参数）.以坐标原点 $O$ 为极点， $x$ 轴的非负半轴为极轴建立极坐标系，直线 $C_{2}$ 的极坐标方程为 $ρ c o s (θ + \frac{π}{4}) = \sqrt{2}$ .

(1)、求曲线 $C_{1}$ 的普通方程和直线 $C_{2}$ 的直角坐标方程；

(2)、已知点 $P$ 的极坐标为 $(2 ， - \frac{π}{2})$ ，设曲线 $C_{1}$ 和直线 $C_{2}$ 交于 $M$ ， $N$ 两点，求 $\frac{1}{| P M |} + \frac{1}{| P N |}$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x - m | + | x + 3 |$

(1)、当 $m = 1$ 时，求不等式 $f (x) \geq 6$ 的解集；

(2)、若关于x的不等式 $f (x) \leq 2 m - 5$ 有解，求实数m的取值范围.

查看试题解析