陕西省2022届高三下学期理数二模预测试卷

试卷更新日期：2022-04-12 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 2 x - 8 \leq 0} ， B = {x | \frac{x - 2}{x + 3} \leq 0}$ ，则 $A ∪ B =$ （）

A、 ${x | - 4 \leq x \leq 2}$ B、 ${x | - 4 \leq x \leq 2$ 且 $x \neq - 3}$ C、 ${x | - 3 \leq x \leq 4}$ D、 ${x | - 3 < x \leq 4}$

查看试题解析
2. 已知复数z满足 $(1 + 2 i) z = 5 \bar{z} - 10 i$ ，则 $| z | =$ （）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{5}$ D、 $2 \sqrt{2}$

查看试题解析
3. 命题 $p ： \forall x \in [1 ， 2] ， 2^{x} \geq 3$ ，命题 $q ： \exists x_{0} \in [1 ， 2] ， l o g_{2} x_{0} \geq 1$ ，则下列命题为真命题的是（）

A、 $p \land q$ B、 $(\neg p) \land (\neg q)$ C、 $p \lor q$ D、 $p \lor (\neg q)$

查看试题解析
4. 若 $(1 + m x^{2}) (1 + x)^{4}$ 的展开式中 $x^{3}$ 的系数为12，则实数 $m =$ （）

A、1 B、2 C、3 D、4

查看试题解析
5. 已知 $f (x)$ 是 $R$ 上的奇函数，当 $x < 0$ 时， $f (x) = - e^{- 3 x}$ ，则 $f (l n 2) =$ （）

A、 $e^{8}$ B、8 C、6 D、 $l n 2$

查看试题解析
6. 把函数 $f (x) = c o s^{2} x - s i n^{2} x$ 的图象向左平移 $\frac{π}{12}$ 个单位长度得到函数 $g (x)$ 的图象，若 $g (x)$ 在 $[0 ， a]$ 上是减函数，则实数a的最大值为（）

A、 $\frac{5 π}{12}$ B、 $\frac{π}{3}$ C、 $\frac{π}{6}$ D、 $\frac{π}{12}$

查看试题解析
7. 如图，在直三棱柱 $A B D - A_{1} B_{1} D_{1}$ 中， $A B = A D = A A_{1} ， ∠ A B D = 45 °$ ， P为 $B_{1} D_{1}$ 的中点，则直线 $P B$ 与 $A D_{1}$ 所成的角为（）

A、30º B、45º C、60º D、90º

查看试题解析
8. 高三（1）班举行英语演讲比赛，共有六名同学进入决赛，在安排出场顺序时，甲排在后三位，且丙、丁排在一起的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{6}$ C、 $\frac{39}{180}$ D、 $\frac{47}{180}$

查看试题解析
9. 已知 $△ A B C$ 的内角A，B，C所对的边分别为a，b，c，且 $C = 60 °$ ， $a = 3$ ， $S_{△ A B C} = \frac{15 \sqrt{3}}{4}$ ，则 $A B$ 边上的中线长为（）

A、49 B、7 C、 $\frac{49}{4}$ D、 $\frac{7}{2}$

查看试题解析
10. 已知圆 $C ： (x - 1)^{2} + (y - 1)^{2} = 4$ ， P为直线 $l ： 2 x + y + 2 = 0$ 上的动点，过点P作圆C的切线 $P A$ ，切点为A，当 $△ P A C$ 的面积最小时， $△ P A C$ 的外接圆的方程为（）

A、 ${(x - \frac{1}{2})}^{2} + {(y - \frac{1}{2})}^{2} = \frac{5}{4}$ B、 ${(x - \frac{1}{2})}^{2} + {(y - \frac{1}{2})}^{2} = \frac{9}{4}$ C、 $x^{2} + {(y - \frac{1}{2})}^{2} = \frac{5}{4}$ D、 ${(x - \frac{1}{2})}^{2} + y^{2} = \frac{5}{4}$

查看试题解析
11. 已知抛物线 $C ： y^{2} = 2 x$ ，过焦点的直线l与C交于A，B两点，若以 $A B$ 为直径的圆与C的准线切于点 $M (- \frac{1}{2} ， \frac{1}{2})$ ，则l的方程为（）

A、 $x - 2 y + 1 = 0$ B、 $x - 2 y - 1 = 0$ C、 $2 x - y + 1 = 0$ D、 $2 x - y - 1 = 0$

查看试题解析
12. 已知函数 $f (x) = | x + 1 | + | x - 1 | + 2 c o s x$ ，若函数 $g (x) = f (x) - a$ 恰有三个零点时， $m + n = a$ （其中m，n为正实数），则 $\frac{7}{m + 1} + \frac{28}{n + 2}$ 的最小值为（）

A、9 B、7 C、 $\frac{30}{7}$ D、4

查看试题解析

二、填空题

13. 已知向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $60 °$ ，且 $\vec{a} = (\frac{1}{2} ， \frac{\sqrt{3}}{2})$ ， $| 2 \vec{a} - \vec{b} | = \sqrt{3}$ ，则 $| \vec{b} | =$ ．

查看试题解析
14. 已知 $α$ 为锐角，若 $s i n (α + \frac{3 π}{2}) = - \frac{1}{3}$ ，则 $c o s (α - \frac{π}{4}) =$ ．

查看试题解析
15. 已知 $F_{1} ， F_{2}$ 是双曲线C的左右焦点，P为C上一点， $| P F_{1} | = 3 | P F_{2} |$ ，且 $c o s ∠ P F_{1} F_{2} = \frac{2 \sqrt{2}}{3}$ ，则C的离心率为．

查看试题解析
16. 在四棱锥 $P - A B C D$ 中，底面是边长为2的正方形， $∠ P D C = ∠ A P D = 90 °$ ， $P A = P D$ ，则以该四棱锥外接球的球心为球心且与平面 $P B C$ 相切的球的体积为．

查看试题解析

三、解答题

17. 已知正项等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{1} = 1 ， 2 a_{1} + a_{2} = a_{3}$ ，数列 ${b_{n}}$ 满足 $2^{b_{n}} = 4 a_{n} (S_{n} + 1)$ ．

(1)、证明：数列 ${b_{n}}$ 为等差数列；

(2)、记 $T_{n}$ 为数列 ${\frac{1}{b_{n} b_{n + 1}}}$ 的前n项和，证明： $\frac{1}{15} \leq T_{n} < \frac{1}{6}$ ．

查看试题解析
18. 随着人民生活水平的日益提高，汽车普遍进入千家万户，尤其在近几年，新能源汽车涌入市场，越来越受到人们喜欢．某新能源汽车销售企业在2017年至2021年的销售量y（单位：万辆）数据如表所示．
年份
2017年
2018年
2019年
2020年
2021年
年份代号x
1
2
3
4
5
销售量y/万辆
17
18
20
22
23
参考数据：含 $\sum_{i = 1}^{5} (x_{i} - \bar{x}) (y_{i} - \bar{y}) = 16$ ， $\sum_{i = 1}^{5} {(x_{i} - \bar{x})}^{2} = 10$ ， $\sum_{i = 1}^{5} {(y_{i} - \bar{y})}^{2} = 26$ ， $\sqrt{65} \approx 8.06$ ．
参考公式：相关系数 $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ， $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ，其中 $\bar{x} ， \bar{y}$ 为样本平均值，线性回归方程也可写为 $\hat{y} = \hat{b} x + \hat{a}$ ．

(1)、根据数据资料，可用线性回归模型拟合y与x的关系，请用相关系数加以说明；

(2)、求出y关于x的线性回归方程，并预计2022年该新能源汽车销售企业的销售量为多少万辆？

查看试题解析
19. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2，E，F分别为 $B D$ 和 $B B_{1}$ 的中点，P为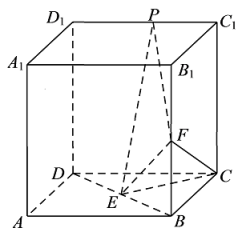棱 $C_{1} D_{1}$ 上的动点．

(1)、是否存在点P使 $P E ⊥$ 平面 $E F C$ ？若存在，求出满足条件时 $C_{1} P$ 的长度并证明；若不存在，请说明理由；

(2)、当 $C_{1} P$ 为何值时，平面 $B C C_{1} B_{1}$ 与平面 $P E F$ 所成锐二面角的正弦值最小．

查看试题解析
20. 已知函数 $f (x) = e^{x} - a x^{2} - x - 1$ ．

(1)、当 $a = - 1$ 时，讨论 $f (x)$ 的单调性；

(2)、当 $x \geq 0$ 时， $f (x) \geq \frac{1}{2} x^{3} - 2 a x^{2}$ 恒成立，求实数a的取值范围．

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的四个顶点围成的四边形的面积为 $4 \sqrt{3}$ ，椭圆C的左、右焦点分别为 $F_{1} (- c ， 0) ， F_{2} (c ， 0)$ ，且 $F_{1}$ 到直线 $b x - c y = 0$ 的距离为 $\frac{\sqrt{3}}{2} c$ ，若直线l与C有且只有一个公共点P，且点P不在x轴上，过点 $F_{1}$ 作l的垂线，垂足为Q，

(1)、求椭圆C的方程；

(2)、求 $△ Q F_{1} F_{2}$ 面积的最大值．

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线l的参数方程为 ${\begin{array}{l} x = 3 + \sqrt{3} t ， \\ y = \sqrt{3} + t \end{array}$ （t是参数）．以O为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为 $ρ^{2} + 5 ρ^{2} s i n^{2} θ - 36 = 0$ ．

(1)、求l的极坐标方程和C的直角坐标方程；

(2)、若l与C交于A，B两点，求 $\frac{1}{| O A |} + \frac{1}{| O B |}$ 的值．

查看试题解析
23. 设 $x$ 、 $y$ 、 $z$ 为正实数，且 $x + y + z = 4$ .

(1)、证明： $\sqrt{x y} + \sqrt{x z} \leq 2 \sqrt{2}$ ；

(2)、证明： ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} \geq \frac{4}{3}$ ．

查看试题解析

年份	2017年	2018年	2019年	2020年	2021年
年份代号x	1	2	3	4	5
销售量y/万辆	17	18	20	22	23