江西省八所重点中学2022届高三理数4月联考试卷

试卷更新日期：2022-04-12 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 2 x - 3 \leq 0}$ ， $B = {x | l g x > 0}$ ，则 $A ∩ B =$ （）

A、 $(- 1 ， 3]$ B、 $(- \infty ， 3]$ C、 $(1 ， 3]$ D、 $[1 ， + \infty)$

查看试题解析
2. 棣莫弗公式 $(c o s x + i s i n x)^{n} = c o s n x + i s i n n x$ （其中 $i$ 为虚数单位）是由法国数学家棣莫弗（1667-1754年）发现的，根据棣茣弗公式可知，复数 ${(c o s \frac{π}{6} + i s i n \frac{π}{6})}^{7}$ 在复平面内所对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 北京时间2月20日，北京冬奥会比赛日收官，中国代表团最终以9枚金牌4枚银牌2枚铜共15枚奖牌的总成绩，排名奖牌榜第三，创造新的历史.据统计某高校共有本科生1600人，硕士生600人，博士生200人申请报名做志愿者，现用分层抽样方法从中抽取博士生30人，则该高校抽取的志愿者总人数为（）

A、300 B、320 C、340 D、360

查看试题解析
4. 魏晋南北朝时期，我国数学家祖冲之利用割圆术，求出圆周率 $π$ 约为 $\frac{355}{113}$ ，是当时世界上最精确的圆周率结果，直到近千年后这一记录才被打破.若已知 $π$ 的近似值还可以表示成 $4 c o s 3 8^{∘}$ ，则 $\frac{π \sqrt{16 - π^{2}}}{1 - 2 s i n^{2} 7^{∘}}$ 的值为（）

A、 $\frac{1}{8}$ B、 $- \frac{1}{8}$ C、8 D、-8

查看试题解析
5. 设 $a = l o g_{2022} 44 ， e^{b} = \frac{2021}{2022} ， c = l n \sqrt{3}$ ，则（）

A、 $c > a > b$ B、 $c > b > a$ C、 $a > b > c$ D、 $a > c > b$

查看试题解析
6. 若正实数 $x ， y$ 满足 ${\begin{array}{l} 2 x + y > 4 \\ 2 x - y < 4 \end{array}$ ，则 $z = x - 3 y$ 的值可能为（）

A、1 B、2 C、3 D、4

查看试题解析
7. 已知圆 $C ： (x - 1)^{2} + (y + 2 \sqrt{2})^{2} = 16$ 和两点 $A (0 ， - m) ､ B (0 ， m)$ ，若圆 $C$ 上存在点 $P$ ，使得 $A P ⊥ B P$ ，则 $m$ 的最大值为（）

A、5 B、6 C、7 D、8

查看试题解析
8. “ $0 < θ < π$ ”是“方程 $\frac{x^{2}}{3} + \frac{y^{2}}{4 s i n θ} = 1$ 表示椭圆”的（）

A、充分不必要条件 B、必要不充分杂件 C、充要杂件 D、既不充分也不必要条件

查看试题解析
9. 在 $△ A B C$ 中，角 $A ， B ， C$ 所对的边分別为 $a ， b ， c$ ，满足 $b + c = 2 a s i n (C + \frac{π}{6})$ ，若函数 $f (x) = s i n (2 x + φ) (| φ | < \frac{π}{2})$ 的图象向左平移 $A$ 个单位长度后的图象于 $y$ 轴对称，则 $f (x)$ 在 $[0 ， \frac{3}{2} A]$ 的值域为（）

A、 $[- 1 ， 1]$ B、 $[- \frac{1}{2} ， 1]$ C、 $[- 1 ， \frac{1}{2}]$ D、 $[- \frac{1}{2} ， \frac{1}{2}]$

查看试题解析
10. 已知 $F_{1} ， F_{2}$ 为椭圆和双曲线的公共焦点， $P$ 是它们的公共点，且 $∠ F_{1} P F_{2} = \frac{π}{3} ， e_{1} ， e_{2}$ 分别为椭圆和双曲线的离心率，则 $\frac{4 e_{1} e_{2}}{\sqrt{3 e_{1}^{2} + e_{2}^{2}}}$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 如图，正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $2 \sqrt{2}$ ，点 $P$ 是 $△ B_{1} C D_{1}$ 内部（不包括边界）的动点.若 $B D ⊥ A P$ ，则线段 $A P$ 长度的取值不可能为（）

A、 $\frac{5}{2}$ B、 $\frac{4}{3} \sqrt{6}$ C、 $2 \sqrt{3}$ D、 $\sqrt{15}$

查看试题解析
12. 已知函数 $f (x) = l o g_{3} (3^{x} + 1) + m x (m \in R)$ 是偶函数，函数 $g (x) = 2 e^{(k - 1) x} - 3 l n x + (3 k - 5) x$ ，若 $g (x) \geq 2 m + 1$ 恒成立，则实数 $k$ 的取值范围是（）

A、 $[1 + e ， + ∞)$ B、 $[1 + \frac{1}{e} ， + ∞)$ C、 $[2 + e ， + ∞)$ D、 $[2 + \frac{1}{e} ， + ∞)$

查看试题解析

二、填空题

13. 已知 $\vec{a} = (1 ， - 1) ， \vec{a} ⊥ \vec{b}$ ，试写出一个满足条件的 $\vec{b} =$ .

查看试题解析
14. 如图，方格蜘蛛网是由一族正方形环绕而成的图形.每个正方形的四个顶点都在其外接正方形的四边上，且分边长为 $3 ： 4$ .现用24米长的铁丝材料制作一个方格蜘蛛网，若最外边的正方形边长为2米，由外到内顺序制作，则完整的正方形的个数最多为.（参考据： $l g 7 \approx 0.85 ， l g 5 \approx 0.70$ ）

查看试题解析
15. 下列命题中，真命题的序号是.
①已知函数 $f (x)$ 满足 $f (\sqrt{x} - 1) = 2 x + 1$ ，则函数 $f (x) = 2 x^{2} + 4 x + 3$ ：
②从分别标有 $1 ， 2 ， 3 ， \dots ， 9$ 的9个完全相同的小球中不放回地随机摸球2次，每次摸球1个，则摸到的2个球上的数字奇偶性相同的概率是 $\frac{4}{9}$ ；
③用数学归纳法证明“ $\frac{1}{n + 1} + \frac{1}{n + 2} + \frac{1}{n + 3} + ⋯ + \frac{1}{2 n} \geq \frac{1}{2} (n \in N^{*})$ ”，由 $n = k$ 到 $n = k + 1$ 时，不等式左边应添加的项是 $\frac{1}{2 k + 1} - \frac{1}{2 k + 2}$ ；
④ ${(2021 \sqrt[3]{x} + \frac{2022}{\sqrt{x}})}^{18}$ 的二项展开式中，共有3个有理项.

查看试题解析
16. 已知正数 $x ， y$ 满足 $\frac{x}{y} + \frac{y}{x} = \frac{6}{x y} - \sqrt{2} ， z = (x + y) (\sqrt{12 - x^{2}} + \sqrt{12 - y^{2}})$ ，则 $z$ 的取值范围是.

查看试题解析

三、解答题

17. 2022年是中国共产主义青年团建团100周年.100年栉风沐雨，共青团始终坚定不移跟党走，团结带领共青团员和广大青年前赴后继､勇当先锋，书写了中国青年运动的华章.实践证明，共青团不愧为党和人民事业的生力军和突击队，不愧为党的得力助手和可靠后备军.为庆祝共青团建团100周年，我校举行团史知识竞赛活动，比赛共20道题，答对一题得5分，答错一题扣2分，学生李华参加了这次活动，假设每道题李华能答对的概率都是 $\frac{3}{4}$ ，且每道题答对与否相互独立.

(1)、求李华开始答题后直到第3题才答对的概率：

(2)、求李华得分的期望值.

查看试题解析
18. 已知函数 $f (x) = \frac{(s i n x - c o s x)^{2} - 1}{s i n^{2} x - c o s^{2} x}$ ，方程 $f (x) = 1$ 在 $(0 ， + ∞)$ 上的解按从小到大的顺序排成数列 ${p_{n}} (n \in N^{*})$ .

(1)、求数列 ${p_{n}}$ 的通项公式；

(2)、设 $q_{n} = \frac{8 p_{n}}{(4 n - 3) (4 n^{2} - 1)}$ ，数列 ${q_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求证： $T_{n} < \frac{π}{2}$ .

查看试题解析
19. 已知过点 $P (2 ， 0)$ 的动直线与抛物线 $C ： y^{2} = 2 p x (p > 0)$ 交于点 $A ， B$ ，抛物线 $C$ 的焦点为 $F$ ，当点 $A$ 横坐标为 $\frac{3}{2}$ 时， $| A F | = 2$ .

(1)、求抛物线 $C$ 的方程；

(2)、当直线 $A B$ 变动时， $x$ 轴上是否存在点 $Q$ ，使得点 $P$ 到直线 $A Q ， B Q$ 的距离相等，若存在，求出点 $Q$ 坐标；若不存在，说明理由.

查看试题解析
20. 阅读以下材料：球的体积公式的推导，球面可以看作一个半圆绕着其直径所在直线旋转一周所得，已知半圆方程为 $x^{2} + y^{2} = R^{2} (y \geq 0)$ ，由 $x^{2} + y^{2} = R^{2} (y \geq 0)$ 得 $y = f (x) = \sqrt{R^{2} - x^{2}}$ ，则 $V = π \int_{- R}^{R} f^{2} (x) d x = π \int_{- R}^{R} (R^{2} - x^{2}) d x = {π (R^{2} x - \frac{x^{3}}{3}) |}_{- R}^{R} = π [(R^{3} - \frac{R^{3}}{3}) - (- R^{3} + \frac{R^{3}}{3})] = \frac{4}{3} π R^{3}$ 根据以上材料，解答下列问题：椭球面可以看成半个椭圆绕着其长轴所在直线蔙转一周所形成的旋转体，定义椭球的扁率 $α (0 < α < 1)$ 为对应椭圆的长､短半轴之差与长半轴之比，通常用扁率 $α$ 来表示椭球的扁平程度，椭球的扁率 $α$ 越大，杯球愈扁.

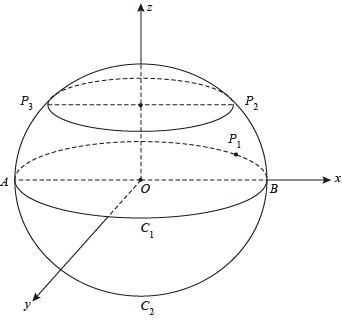(1)、若椭圆方程为 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，试推导椭球的体积公式：

(2)、如图所示的椭球是由水平放置的椭圆 $C_{1}$ 绕其长轴 $A B$ 所在直线旋转所得，其中旋转 $90 °$ 得到椭圆 $C_{2}$ ，椭圆 $C_{1}$ 上的点 $P_{1}$ 刚好对应椭圆 $C_{2}$ 上的点 $P_{2}$ ，椭圆 $C_{1}$ 的中心为 $O$ ，以 $O B$ 为 $x$ 轴建立空间直角坐标系 $O - x y z$ （椭圆 $C_{1}$ 在平面 $x O y$ 内），点 $P_{2}$ 关于 $z$ 轴对称的点为 $P_{3}$ ，已知椭球体积为 $\frac{8}{3} π$ ，椭球扁率值为 $\frac{1}{2} ， P_{1}$ 横坐标为1，纵坐标为负数，求平面 $A B P_{3}$ 与平面 $P_{1} B P_{3}$ 所成锐二面角的余弦值.

查看试题解析
21. 已知函数 $f (x) = \frac{1}{2} x^{2} - a x + l n x (a \in R)$ .

(1)、试讨论函数 $f (x)$ 的单调性：

(2)、设 $a \leq \frac{10}{3} ， m ， n$ 分别是 $f (x)$ 的极大值和极小值，且 $S = m - n$ ，求 $S$ 的取值范围.

查看试题解析
22. 在直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = 1 + 3 t \\ y = 2 - 4 t \end{array}$ （ $t$ 为参数），以坐标原点为极点，以 $x$ 轴的非负半轴为极轴，建立极坐标系，曲线 $C$ 的极坐标方程为 $ρ^{2} - 2 ρ c o s θ - 6 ρ s i n θ + 8 = 0$ ，已知直线 $l$ 与曲线 $C$ 交于不同的两点 $M ， N$ .

(1)、求直线 $l$ 的普通方程的一般形式和曲线 $C$ 的直角坐标方程：

(2)、设 $P (1 ， 2)$ ，求 $\frac{| P N |}{| P M |} + \frac{| P M |}{| P N |}$ 的值.

查看试题解析
23. 设函数 $f (x) = | x + 3 | + | 2 x - 2 |$ .

(1)、求不等式 $f (x) > 5$ 的解集；

(2)、若 $f (x)$ 的最小值是 $m$ ，且 $3 a + 4 b + 5 c = m$ ，求 $a^{2} + b^{2} + c^{2}$ 的最小值.

查看试题解析