湖北省十一校2022届高三下学期数学第二次联考试卷

试卷更新日期：2022-04-12 类型：高考模拟

进入出卷网下载

一、单选题

1. 若全集 $U = R$ ，集合 $A = {0 ， 1 ， 2 ， 3 ， 4 ， 5}$ ， $B = {x | x < 3}$ ，则图中阴影部分表示的集合为（）

A、 ${3 ， 4 ， 5}$ B、 ${0 ， 1 ， 2}$ C、 ${0 ， 1 ， 2 ， 3}$ D、 ${4 ， 5}$

查看试题解析
2. 直线 $k x + y - 2 - 3 k = 0$ 与圆 $x^{2} + y^{2} - 4 x - 5 = 0$ 的位置关系是（）

A、相离 B、相切 C、相交 D、相交或相切

查看试题解析
3. 祖暅原理：“幂势既同，则积不容异”.它是中国古代一个涉及几何体体积的问题，意思是两个同高的几何体，如在等高处的截面面积恒相等，则体积相等.设A，B为两个同高的几何体，p：A，B的体积相等，q：A，B在等高处的截面面积恒相等，根据祖暅原理可知，p是q的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 定义：24小时内降水在平地上积水厚度（ $mm$ ）来判断降雨程度．其中小雨（ $< 10 mm$ ），中雨（ $10 mm - 25 mm$ ），大雨（ $25 mm - 50 mm$ ），暴雨（ $50 mm - 100 mm$ ），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）

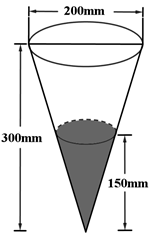A、小雨 B、中雨 C、大雨 D、暴雨

查看试题解析
5. 已知a， $b$ 为正实数，直线 $y = x - 2 a$ 与曲线 $y = l n (x + b)$ 相切，则 $\frac{1}{a} + \frac{2}{b}$ 的最小值是（）

A、6 B、 $4 \sqrt{2}$ C、8 D、 $2 \sqrt{2}$

查看试题解析
6. 如图为宜昌市至喜长江大桥，其缆索两端固定在两侧索塔顶部，中间形成的平面曲线称为悬链线．当微积分尚未出现时，伽利略猜测这种形状是抛物线，直到1691年莱布尼兹和伯努利借助微积分推导出悬链线的方程 $y = \frac{c}{2} \cdot (e^{\frac{x}{c}} + e^{- \frac{x}{c}})$ ，其中 $c$ 为参数．当 $c = 1$ 时，函数 $c o s h (x) = \frac{e^{x} + e^{- x}}{2}$ 称为双曲余弦函数，与之对应的函数 $s i n h (x) = \frac{e^{x} - e^{- x}}{2}$ 称为双曲正弦函数．关于双曲函数，下列结论正确的是（）

A、 ${[s i n h (x)]}^{2} - {[c o s h (x)]}^{2} = 1$ B、 $(c o s h (x))^{'} = - s i n h (x)$ C、 $c o s h (- 1) > c o s h (2)$ D、 $s i n h (- x) = - s i n h (x)$

查看试题解析
7. 已知双曲线 $C$ ： $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ （ $a > 0$ ， $b > 0$ ）的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，过 $F_{1}$ 的直线与 $C$ 的左支交于 $A$ 、 $B$ 两点，且 $\overset{⇀}{A F_{1}} = 3 \vec{F_{1} B}$ ， $∠ A B F_{2} = 90 °$ ，则 $C$ 的渐近线方程为（）

A、 $y = \pm 2 x$ B、 $y = \pm \sqrt{5} x$ C、 $y = \pm \frac{\sqrt{6}}{2} x$ D、 $y = \pm \frac{\sqrt{10}}{2} x$

查看试题解析
8. 已知 $α$ 、 $β$ 、 $γ$ 、 $δ$ 为锐角，在 $s i n α c o s β$ ， $s i n β c o s γ$ ， $s i n γ c o s δ$ ， $s i n δ c o s α$ 四个值中，大于 $\frac{1}{2}$ 的个数的最大值记为 $m$ ，小于 $\frac{1}{4}$ 的个数的最大值记为 $n$ ，则 $m + n$ 等于（）

A、8 B、7 C、6 D、5

查看试题解析

二、多选题

9. 如图，5个数据 $(x ， y)$ ，去掉点 $D (3 ， 10)$ 后，下列说法正确的是（）

A、相关系数r变大 B、残差平方和变大 C、变量x与变量y呈正相关 D、变量x与变量y的相关性变强

查看试题解析
10. 平行四边形 $A B C D$ 中， $A B > A D$ ，将三角形 $A B D$ 沿着 $B D$ 翻折至三角形 $A^{'} B D$ ，则下列直线中有可能与直线 $A^{'} B$ 垂直的是（）

A、直线 $B C$ B、直线 $C D$ C、直线 $B D$ D、直线 $A^{'} C$

查看试题解析
11. 数列 ${a_{n}}$ 的前 $n$ 项为 $S_{n}$ ，已知 $4 S_{n} = a_{n}^{2} + 2 a_{n} + 1$ ，下列说法中正确的是（）

A、 ${a_{n}}$ 为等差数列 B、 ${a_{n}}$ 可能为等比数列 C、 ${a_{n}}$ 为等差数列或等比数列 D、 ${a_{n}}$ 可能既不是等差数列也不是等比数列

查看试题解析
12. 如下图所示，B是AC的中点， $\vec{B E} = 2 \vec{O B}$ ， P是平行四边形BCDE内 $($ 含边界 $)$ 的一点，且 $\vec{O P} = x \vec{O A} + y \vec{O B} (x ， y \in R)$ ，以下结论中正确的是（）

A、当P是线段CE的中点时， $x = - \frac{1}{2}$ ， $y = \frac{9}{4}$ B、当 $x = - \frac{1}{2}$ 时， $y \in [\frac{3}{2} ， 4]$ C、若 $x + y$ 为定值2时，则在平面直角坐标系中，点P的轨迹是一条线段 D、 $x - y$ 的最大值为-1

查看试题解析

三、填空题

13. 设复数z满足 $(1 + i) z = 2 i$ （其中 $i$ 是虚数单位），则 $| z | =$ .

查看试题解析
14. $8^{11}$ 除以9的余数是.

查看试题解析
15. 已知函数 $f (x) = 2 s i n (2 x + \frac{π}{6}) - m$ ， $x \in [0 ， \frac{7 π}{6}]$ 有三个不同的零点 $x_{1} ， x_{2} ， x_{3}$ ，且 $x_{1} < x_{2} < x_{3}$ ，则 $m (x_{1} + 2 x_{2} + x_{3})$ 的范围是.

查看试题解析
16. 若指数函数 $y = a^{x}$ （ $a > 0$ 且 $a \neq 1$ ）与三次函数 $y = x^{3}$ 的图象恰好有两个不同的交点，则实数 $a$ 的取值范围是.

查看试题解析

四、解答题

17. 如图，在四边形 $A B C D$ 中， $A B // C D$ ， $A B = 2 \sqrt{6}$ ， $C D = \sqrt{6}$ ， $\cos A = \frac{\sqrt{6}}{3}$ ， $\cos ∠ A D B = \frac{1}{3}$ .

(1)、求 $\cos ∠ B D C$ ；

(2)、求 $B C$ 的长.

查看试题解析
18. 已知等差数列 ${a_{n}}$ 满足 $a_{1} + a_{2} = 10$ ， $a_{4} - a_{3} = 2$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设等比数列 ${b_{n}}$ 满足 $b_{2} = a_{3}$ ， $b_{3} = a_{7}$ 设 $c_{n} = 5 a_{n} - b_{n}$ ，数列 ${c_{n}}$ 的前n项和为 $S_{n}$ ，求 $S_{n}$ 的最大值.

查看试题解析
19. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，四边形 $A A_{1} C_{1} C$ 是边长为 $4$ 的正方形， $A B = 3$ .再从条件①､条件②､条件③中选择两个能解决下面问题的条件作为已知，并作答.
条件①： $B C = 5$ ；条件②： $A B ⊥ A A_{1}$ ；条件③：平面 $A B C ⊥$ 平面 $A A_{1} C_{1} C$ .

(1)、求证： $A B ⊥$ 平面 $A A_{1} C_{1} C$ ；

(2)、求直线 $B C$ 与平面 $A_{1} B C_{1}$ 所成角的正弦值.

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 过点 $(0 ， 1)$ ，离心率为 $\frac{\sqrt{2}}{2}$ ．

(1)、求椭圆 $C$ 的方程；

(2)、直线 $y = k (x + 1) (k \neq 0)$ 与椭圆交于 $A$ 、 $B$ 两点，过 $A$ 、 $B$ 作直线 $l ： x = - 2$ 的垂线，垂足分别为 $M$ 、 $N$ ，点 $G$ 为线段 $M N$ 的中点， $F$ 为椭圆 $C$ 的左焦点．求证：四边形 $A G N F$ 为梯形．

查看试题解析
21. 某中学在2020年高考分数公布后对高三年级各班的成绩进行分析.经统计某班有 $50$ 名同学，总分都在区间 $[600 ， 700]$ 内，将得分区间平均分成 $5$ 组，统计频数､频率后，得到了如图所示的“频率分布”折线图.

(1)、请根据频率分布折线图，画出频率分布直方图，并根据频率分布直方图估计该班级的平均分；

(2)、经过相关部门的计算，本次高考总分大于等于 $680$ 的同学可以获得高校 $T$ 的“强基计划”入围资格.高校 $T$ 的“强基计划”校考分为两轮.第一轮为笔试，所有入围同学都要参加，考试科目为数学和物理，每科的笔试成绩从高到低依次有 $A^{+}$ ， $A$ ， $B$ ， $C$ 四个等级，两科中至少有一科得到 $A^{+}$ ，且两科均不低于 $B$ ，才能进入第二轮，第二轮得到“通过的同学将被高校 $T$ 提前录取.已知入围的同学参加第一轮笔试时，总分高于 $690$ 分的同学在每科笔试中取得 $A^{+}$ ， $A$ ， $B$ ， $C$ 的概率分别为 $\frac{2}{3}$ ， $\frac{1}{6}$ ， $\frac{1}{12}$ ， $\frac{1}{12}$ ；总分不超过 $690$ 分的同学在每科笔试中取得 $A^{+}$ ， $A$ ， $B$ ， $C$ 的概率分别为 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{6}$ ， $\frac{1}{4}$ ；进入第二轮的同学，若两科笔试成绩均为 $A^{+}$ ，则免面试，并被高校 $T$ 提前录取；若两科笔试成绩只有一个 $A^{+}$ ，则要参加面试，总分高于 $690$ 分的同学面试“通过”的概率为 $\frac{2}{3}$ ，总分不超过 $690$ 分的同学面试“通过”的概率为 $\frac{2}{5}$ ，面试“通过”的同学也将被高校 $T$ 提前录取.若该班级考分前 $10$ 名都已经报考了高校 $T$ 的“强基计划”，且恰有 $2$ 人成绩高于 $690$ 分.求
①总分高于 $690$ 分的某位同学没有进入第二轮的概率 $P_{1}$ ；
②该班恰有两名同学通过“强基计划”被高校 $T$ 提前录取的概率 $P_{2}$ .

查看试题解析
22. 对于正实数 $a ， b (a > b)$ ，熟知基本不等式： $G (a ， b) < A (a ， b)$ ，其中 $A (a ， b) = \frac{a + b}{2}$ 为 $a ， b$ 的算术平均数， $G (a ， b) = \sqrt{a b}$ 为 $a ， b$ 的几何平均数．现定义 $a ， b$ 的对数平均数： $L (a ， b) = \frac{a - b}{l n a - l n b} ．$

(1)、设 $x > 1$ ，求证： $l n x < \frac{1}{2} (x - \frac{1}{x})$ ：

(2)、①利用第（1）小问证明不等式： $G (a ， b) < L (a ， b)$ ：
②若不等式 $k \cdot L (a ， b) < G (a ， b) + A (a ， b)$ 对于任意的正实数 $a ， b (a > b)$ 恒成立，求正实数 $k$ 的最大值．

查看试题解析