广东省2022届高三数学一模试卷
试卷更新日期:2022-04-12 类型:高考模拟
一、单选题
-
1. 已知复数 , 其中是虚数单位,则( )A、2 B、3 C、4 D、52. 若向量 , 满足 , , , 则( )A、 B、2 C、2 D、43. 已知为锐角,且 , 则( )A、 B、 C、 D、4. 为解决皮尺长度不够的问题,实验小组利用自行车来测量A,B两点之间的直线距离.如下图,先将自行车前轮置于点A,前轮上与点A接触的地方标记为点C,然后推着自行车沿AB直线前进(车身始终保持与地面垂直),直到前轮与点B接触.经观测,在前进过程中,前轮上的标记点C与地面接触了10次,当前轮与点B接触时,标记点C在前轮的左上方(以下图为观察视角),且到地面的垂直高度为0.45m.已知前轮的半径为0.3m,则A,B两点之间的距离约为( )(参考数值:)
 A、20.10m B、19.94m C、19.63m D、19.47m5. 从集合的非空子集中随机选择两个不同的集合A,B,则的概率为( )A、 B、 C、 D、6. 已知函数 , , 则图象如图的函数可能是( )
A、20.10m B、19.94m C、19.63m D、19.47m5. 从集合的非空子集中随机选择两个不同的集合A,B,则的概率为( )A、 B、 C、 D、6. 已知函数 , , 则图象如图的函数可能是( )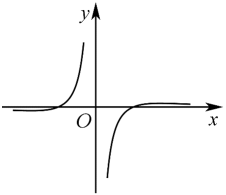 A、 B、 C、 D、7. 已知、是双曲线的左、右焦点,点是双曲线的右顶点,点在过点且斜率为的直线上,为等腰三角形, , 则双曲线的离心率为( )A、 B、2 C、3 D、48. 已知正项数列满足 , 当最大时,的值为( )A、2 B、3 C、4 D、5
A、 B、 C、 D、7. 已知、是双曲线的左、右焦点,点是双曲线的右顶点,点在过点且斜率为的直线上,为等腰三角形, , 则双曲线的离心率为( )A、 B、2 C、3 D、48. 已知正项数列满足 , 当最大时,的值为( )A、2 B、3 C、4 D、5二、多选题
-
9. 设 , 为不同的直线, , 为不同的平面,则下列结论中正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , 则10. 中国正在从电影大国迈向电影强国.下面是2017至2021年各年国内电影票房前十名影片中,国产影片(含合拍片)与进口影片数量统计图,则下列说法中正确的是( )
 A、2017至2021年各年国内电影票房前十名影片中,国产影片数量占比不低于 B、2017至2021年各年国内电影票房前十名影片中,国产影片数量占比逐年提高 C、2017至2021年各年国内电影票房前十名影片中,国产影片数量的平均数大于进口影片数量的平均数 D、2017至2021年各年国内电影票房前十名影片中,国产影片数量的方差等于进口影片数量的方差11. 已知数列满足 , , 则下列结论中正确的是( )A、 B、为等比数列 C、 D、12. 已知抛物线的焦点为F,抛物线C上存在n个点 , , , (且)满足 , 则下列结论中正确的是( )A、时, B、时,的最小值为9 C、时, D、时,的最小值为8
A、2017至2021年各年国内电影票房前十名影片中,国产影片数量占比不低于 B、2017至2021年各年国内电影票房前十名影片中,国产影片数量占比逐年提高 C、2017至2021年各年国内电影票房前十名影片中,国产影片数量的平均数大于进口影片数量的平均数 D、2017至2021年各年国内电影票房前十名影片中,国产影片数量的方差等于进口影片数量的方差11. 已知数列满足 , , 则下列结论中正确的是( )A、 B、为等比数列 C、 D、12. 已知抛物线的焦点为F,抛物线C上存在n个点 , , , (且)满足 , 则下列结论中正确的是( )A、时, B、时,的最小值为9 C、时, D、时,的最小值为8三、填空题
-
13. 二项式展开式中的常数项为.14. 如图为四棱锥的侧面展开图(点 , 重合为点),其中 , , 是线段的中点,请写出四棱锥中一对一定相互垂直的异面直线:.(填上你认为正确的一个结论即可,不必考虑所有可能的情形)
 15. 如图,已知扇形的半径为 , 以为原点建立平面直角坐标系, , , 则的中点的坐标为.
15. 如图,已知扇形的半径为 , 以为原点建立平面直角坐标系, , , 则的中点的坐标为. 16. 已知直线分别与函数和的图象交于点A,B,则的最小值为.
16. 已知直线分别与函数和的图象交于点A,B,则的最小值为.四、解答题
-
17. 在中,角的对边分别为 , 下面给出有关的三个论断:①;②;③.
化简上述三个论断,求出角的值或角的关系,并以其中两个论断作为条件,余下的一个论断作为结论,写出所有可能的真命题.(不必证明)
18. 如图,为圆柱的轴截面,是圆柱上异于 , 的母线. (1)、证明:平面DEF;(2)、若 , 当三棱锥的体积最大时,求二面角的余弦值.19. 已知正项数列 , 其前n项和满足.(1)、求证:数列是等差数列,并求出的表达式;(2)、数列中是否存在连续三项 , , , 使得 , , 构成等差数列?请说明理由.20. 小王每天17:00—18:00都会参加一项自己喜欢的体育运动,运动项目有篮球、羽毛球、游泳三种.已知小王当天参加的运动项目只与前一天参加的运动项目有关,在前一天参加某类运动项目的情况下,当天参加各类运动项目的概率如下表:
(1)、证明:平面DEF;(2)、若 , 当三棱锥的体积最大时,求二面角的余弦值.19. 已知正项数列 , 其前n项和满足.(1)、求证:数列是等差数列,并求出的表达式;(2)、数列中是否存在连续三项 , , , 使得 , , 构成等差数列?请说明理由.20. 小王每天17:00—18:00都会参加一项自己喜欢的体育运动,运动项目有篮球、羽毛球、游泳三种.已知小王当天参加的运动项目只与前一天参加的运动项目有关,在前一天参加某类运动项目的情况下,当天参加各类运动项目的概率如下表:前一天
当天
篮球
羽毛球
游泳
篮球
0.5
0.2
0.3
羽毛球
0.3
0.1
0.6
游泳
0.3
0.6
0.1
(1)、已知小王第一天打羽毛球,则他第三天做哪项运动的可能性最大?(2)、已知小王参加三种体育运动一小时的能量消耗如下表所示:运动项目
篮球
羽毛球
游泳
能量消耗/卡
500
400
600
求小王从第一天打羽毛球开始,前三天参加体育运动能量消耗总数的分布列和期望.