甘肃省平凉市2022届高三理数第二次模拟考试试卷

试卷更新日期：2022-04-12 类型：高考模拟

进入出卷网下载

一、单选题

1. 在复平面内，复数 $z_{1}$ ， $z_{2}$ 对应的点分别是 $(0 ， 2)$ ， $(- 1 ， 1)$ ，则复数 $z_{1} z_{2}$ 的虚部为（）

A、2i B、-2i C、2 D、-2

查看试题解析
2. 设集合 $A = {x | x^{2} - x - 6 \leq 0}$ ， $B = {x | \sqrt{x - 1} < 2}$ ，则 $A ∩ B =$ （）

A、 ${x | - 2 < x < 3}$ B、 ${x | 1 \leq x \leq 3}$ C、 ${x | 1 \leq x < 3}$ D、 ${x | - 2 \leq x \leq 3}$

查看试题解析
3. 已知平面内两定点 $F_{1} (- 3 ， 0)$ ， $F_{2} (3 ， 0)$ ，下列条件中满足动点 $P$ 的轨迹为双曲线的是（）

A、 $| P F_{1} | - | P F_{2} | = \pm 7$ B、 $| P F_{1} | - | P F_{2} | = \pm 6$ C、 $| P F_{1} | - | P F_{2} | = \pm 4$ D、 ${| P F_{1} |}^{2} - {| P F_{2} |}^{2} = \pm 6$

查看试题解析
4. 已知函数 $f (x)$ 的导函数的图象如图所示，则 $f (x)$ 的极值点的个数为（）

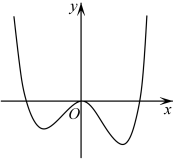A、0 B、1 C、2 D、3

查看试题解析
5. 2022年北京冬奥会结束后，4位德国运动员和5位中国运动员排成一排拍照，则这 $4$ 位德国运动员排在一起的排法数为（）

A、 $A_{6}^{6}$ B、 $A_{4}^{4} A_{5}^{5}$ C、 $A_{5}^{5} A_{6}^{4}$ D、 $A_{4}^{4} A_{6}^{6}$

查看试题解析
6. 已知函数 $f (x) = 3 c o s 2 x$ 的图象向左平移 $\frac{π}{3}$ 个单位长度后得到函数 $g (x)$ 的图象，关于函数 $g (x)$ ，下列选项不正确的是（）

A、最小正周期为 $π$ B、 $g (x) = 3 c o s (2 x + \frac{2 π}{3})$ C、 $g (x)$ 图象的对称中心为 $(\frac{k π}{2} - \frac{π}{12} ， 0) (k \in Z)$ D、当 $x = \frac{k π}{2} - \frac{π}{3} (k \in Z)$ 时， $g (x)$ 取得最大值

查看试题解析
7. 如图，在正方体 $A_{1} B_{1} C_{1} D_{1} - A B C D$ 中， $P$ 为 $C_{1} D_{1}$ 的中点，则过点 $A_{1}$ ， $B$ ， $P$ 的平面截正方体所得的截面的侧视图（阴影部分）为（）

A、 B、 C、 D、

查看试题解析
8. 滕王阁，江南三大名楼之一，因初唐诗人王勃所作《滕王阁序》中的“落霞与孤鹜齐飞，秋水共长天一色”而流芳后世.如图，若某人在点A测得滕王阁顶端仰角为 $30 °$ ，此人往膝王阁方向走了42米到达点B，测得滕王阁顶端的仰角为 $45 °$ ，则滕王阁的高度最接近于（）（忽略人的身高）（参考数据： $\sqrt{3} \approx 1.732$ ）

A、49米 B、51米 C、54米 D、57米

查看试题解析
9. 在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是矩形， $P A ⊥$ 底面 $A B C D$ ，且 $P A = A B$ ， $A D = \sqrt{3} A B$ ，则二面角 $P - C D - B$ 的大小为（）

A、30° B、45° C、60° D、75°

查看试题解析
10. 设 $x ， y$ 满足约束条件 ${\begin{array}{l} x \geq 0 \\ x \in Z \\ y \geq x - 3 \\ y \leq \frac{1}{3} x + 2 \end{array}$ ，则 $z = 2 x + 4 y$ 的最大值为（）

A、 $\frac{94}{3}$ B、30 C、32 D、33

查看试题解析
11. 已知 $\vec{A B} ⊥ \vec{A C} ， 2 | \vec{A B} | = 3 | \vec{A C} | = 6 m （ m ⟩ 0 ，$ 若点M是△ABC所在平面内的一点，且 $A M$ = $\frac{\vec{A B}}{| \vec{A B} |} - \frac{m \vec{A C}}{| \vec{A C} |}$ ，则 $\vec{M B} \cdot \vec{M C}$ 的最小值为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{5}{6}$

查看试题解析
12. 已知定义在R上的奇函数 $f (x)$ 满足 $f (x) = f (e - x)$ ，当 $x \in (0 ， e)$ 时， $f (x) = | x - \frac{e}{2} |$ ，方程 $f (x) - \frac{1}{2 e} (x - e) = 0$ 在区间 $[- e ， 3 e]$ 内所有实根的和为（）

A、 $2 e$ B、 $3 e$ C、 $4 e$ D、 $5 e$

查看试题解析

二、填空题

13. $l o g_{2} 7 \cdot l o g_{7} 8 =$ ．

查看试题解析
14. 已知 $t a n (α + β) = 4 ， t a n β = 2$ ，则 $t a n 2 α =$ .

查看试题解析
15. 某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这100名同学的得分都在 $[50 ， 100]$ 内，按得分分成5组： $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ ，得到如图所示的频率分布直方图，则估计这100名同学的得分的中位数为.

查看试题解析
16. 已知F是椭圆E： $\frac{x^{2}}{4} + \frac{y^{2}}{2} = 1$ 的右焦点，P是椭圆E上一点，Q是圆C： $x^{2} + y^{2} - 2 \sqrt{2} x - 4 \sqrt{2} y + 9 = 0$ 上一点，则 $| P Q | - | P F |$ 的最小值为，此时直线PQ的斜率为.

查看试题解析

三、解答题

17. 一机械制造加工厂的某条生产线设备在正常运行的情况下，生产的零件尺寸z（单位： $m m$ ）服从正态分布 $N (200 ， σ^{2})$ ，且 $P (z \leq 210) = 0.9$ .

(1)、求 $z < 190$ 的概率；

(2)、若从该条生产线上随机选取2个零件，设X表示零件尺寸小于 $190 m m$ 的零件个数，求X的分布列与数学期望.

查看试题解析
18. 如图，在底面为矩形的四棱锥 $P - A B C D$ 中，E为棱 $A D$ 上一点， $P E ⊥$ 底面 $A B C D$ ．

(1)、证明：平面 $P A B ⊥$ 平面 $P A D$ ．

(2)、若 $A E = 2 ， D E = P E = 3$ ，且四棱锥 $P - A B C D$ 的体积为20，求直线 $E C$ 与平面 $P A B$ 所成角的正弦值．

查看试题解析
19. 在① $a_{1} = 1 ， n a_{n + 1} = (n + 1) a_{n}$ ， ② $2^{a_{1}} + 2^{a_{2}} + ⋯ + 2^{a_{n}} = 2^{n + 1} - 2$ 这两个条件中任选一个，补充在下面的问题中并作答
问题：在数列{ $a_{n}$ }中，已知____.

(1)、求{ $a_{n}$ }的通项公式

(2)、若 $b_{n} = \frac{2 a_{n} - 1}{3^{a_{n}}}$ 求数列{ $b_{n}$ }的前n项和 $S_{n}$
注：如果选择两个条件分别解答，按第一个解答计分

查看试题解析
20. 已知抛物线C的焦点F在 $x$ 轴上，过F且垂直于 $x$ 轴的直线交C于A（点 $A$ 在第一象限），B两点，且 $| A B | = 4$ .

(1)、求C的标准方程.

(2)、已知 $l$ 为C的准线，过 $F$ 的直线 $l_{1}$ 交 $C$ 于M， $N$ （M， $N$ 异于A，B）两点，证明：直线AM， $B N$ 和 $l$ 相交于一点.

查看试题解析
21. 已知函数 $f (x) = (a^{2} + 1) l n x + a x - \frac{a}{x}$

(1)、若 $a = 1$ ，求曲线 $y = f (x)$ 在 $x = 1$ 处的切线方程；

(2)、若 $f (x) < 0$ 在（1， $+ \infty$ ）上恒成立，求a的值.

查看试题解析
22. 已知曲线 $C_{1} ： {\begin{array}{l} x = 1 + c o s t \\ y = 1 + s i n t \end{array} (t$ 为参数 $)$ ， $C_{2} ： {\begin{array}{l} x = \sqrt{5} c o s θ \\ y = s i n θ \end{array} (θ$ 为参数 $)$ .

(1)、求 $C_{1} ， C_{2}$ 的普通方程；

(2)、若 $C_{1}$ 上的点 $P$ 对应的参数为 $t = π$ ， $Q$ 为 $C_{2}$ 上一个动点，求 $| P Q |$ 的最大值.

查看试题解析
23. 已知函数 $f (x) = | x - 1 |$ .

(1)、解不等式 $f (x) + | x - 2 | \leq 2$ ；

(2)、若存在 $x \in R$ ，使得 $\frac{4}{f (x)} + f (x) \leq m^{2} - m + 2$ 成立，求 $m$ 的取值范围.

查看试题解析